Physics:Octacube (sculpture)
The Octacube is a large, stainless steel sculpture displayed in the mathematics department of Pennsylvania State University in State College, PA. The sculpture represents a mathematical object called the 24-cell or "octacube". Because a real 24-cell is four-dimensional, the artwork is actually a projection into the three-dimensional world.
Octacube has very high intrinsic symmetry, which matches features in chemistry (molecular symmetry) and physics (quantum field theory).
The sculpture was designed by Adrian Ocneanu (de), a mathematics professor at Pennsylvania State University. The university's machine shop spent over a year completing the intricate metal-work. Octacube was funded by an alumna in memory of her husband, Kermit Anderson, who died in the September 11 attacks.
Artwork
The Octacube's metal skeleton measures about 6 feet (1.8 meters) in all three dimensions. It is a complex arrangement of unpainted, tri-cornered flanges. The base is a 3-foot (0.91-meter) high granite block, with some engraving.[1]
The artwork was designed by Adrian Ocneanu, a Penn State mathematics professor. He supplied the specifications for the sculpture's 96 triangular pieces of stainless steel and for their assembly. Fabrication was done by Penn State's machine shop, led by Jerry Anderson. The work took over a year, involving bending and welding as well as cutting. Discussing the construction, Ocneanu said:[1]
It's very hard to make 12 steel sheets meet perfectly—and conformally—at each of the 23 vertices, with no trace of welding left. The people who built it are really world-class experts and perfectionists—artists in steel.
Because of the reflective metal at different angles, the appearance is pleasantly strange. In some cases, the mirror-like surfaces create an illusion of transparency by showing reflections from unexpected sides of the structure. The sculpture's mathematician creator commented:[1]
When I saw the actual sculpture, I had quite a shock. I never imagined the play of light on the surfaces. There are subtle optical effects that you can feel but can't quite put your finger on.
- Views of the Octacube from multiple angles
Interpretation
Regular shapes
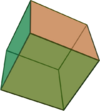
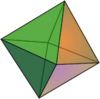
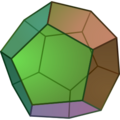
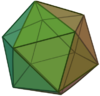
The Platonic solids are three-dimensional shapes with special, high, symmetry. They are the next step up in dimension from the two-dimensional regular polygons (squares, equilateral triangles, etc.). The five Platonic solids are the tetrahedron (4 faces), cube (6 faces), octahedron (8 faces), dodecahedron (12 faces), and icosahedron (20 faces). They have been known since the time of the Ancient Greeks and valued for their aesthetic appeal and philosophical, even mystical, import. (See also the Timaeus, a dialogue of Plato.)
| The Platonic solids | ||||

|
|
|
|
|
| Tetrahedron | Cube | Octahedron | Dodecahedron | Icosahedron |
In higher dimensions, the counterparts of the Platonic solids are the regular polytopes. These shapes were first described in the mid-19th century by a Swiss mathematician, Ludwig Schläfli. In four dimensions, there are six of them: the pentachoron (5-cell), tesseract (8-cell), hexadecachoron (16-cell), octacube (24-cell), hecatonicosachoron (120-cell), and the hexacosichoron (600-cell).
The 24-cell consists of 24 octahedrons, joined in 4-dimensional space. The 24-cell's vertex figure (the 3-D shape formed when a 4-D corner is cut off) is a cube. Despite its suggestive name, the octacube is not the 4-D analog of either the octahedron or the cube. In fact, it is the only one of the six 4-D regular polytopes that lacks a corresponding Platonic solid.[note 1]
| Attempts to picture the 24-cell | ||
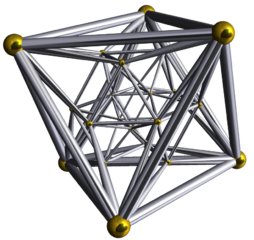
|

| |
| Schlegel diagram | 4-dimensional rotation | |
Projections

Ocneanu explains the conceptual challenge in working in the fourth dimension:[1] "Although mathematicians can work with a fourth dimension abstractly by adding a fourth coordinate to the three that we use to describe a point in space, a fourth spatial dimension is difficult to visualize."
Although it is impossible to see or make 4-dimensional objects, it is possible to map them into lower dimensions to get some impressions of them. An analogy for converting the 4-D 24-cell into its 3-D sculpture is cartographic projection, where the surface of the 3-D Earth (or a globe) is reduced to a flat 2-D plane (a portable map). This is done either with light 'casting a shadow' from the globe onto the map or with some mathematical transformation. Many different types of map projection exist: the familiar rectangular Mercator (used for navigation), the circular gnomonic (first projection invented), and several others. All of them have limitations in that they show some features in a distorted manner—'you can't flatten an orange peel without damaging it'—but they are useful visual aids and convenient references.
In the same manner that the exterior of the Earth is a 2-D skin (bent into the third dimension), the exterior of a 4-dimensional shape is a 3-D space (but folded through hyperspace, the fourth dimension). However, just as the surface of Earth's globe cannot be mapped onto a plane without some distortions, neither can the exterior 3-D shape of the 24-cell 4-D hyper-shape. In the image on the right a 24-cell is shown projected into space as a 3-D object (and then the image is a 2-D rendering of it, with perspective to aid the eye). Some of the distortions:
- Curving edge lines: these are straight in four dimensions, but the projection into a lower dimension makes them appear to curve (similar effects occur when mapping the Earth).
- It is necessary to use semi-transparent faces because of the complexity of the object, so the many "boxes" (octahedral cells) are seen.
- Only 23 cells are clearly seen. The 24th cell is the "outside in", the whole exterior space around the object as seen in three dimensions.
To map the 24-cell, Ocneanu uses a related projection which he calls windowed radial stereographic projection. As with the stereographic projection, there are curved lines shown in 3-D space. Instead of using semitransparent surfaces, "windows" are cut into the faces of the cells so that interior cells can be seen. Also, only 23 vertices are physically present. The 24th vertex "occurs at infinity" because of the projection; what one sees is the 8 legs and arms of the sculpture diverging outwards from the center of the 3-D sculpture.[1]
Symmetry
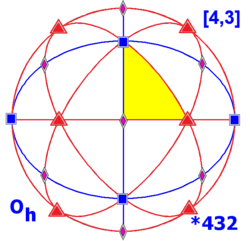
The Octacube sculpture has very high symmetry. The stainless steel structure has the same amount of symmetry as a cube or an octahedron. The artwork can be visualized as related to a cube: the arms and legs of the structure extend to the corners. Imagining an octahedron is more difficult; it involves thinking of the faces of the visualized cube forming the corners of an octahedron. The cube and octahedron have the same amount and type of symmetry: octahedral symmetry, called Oh (order 48) in mathematical notation. Some, but not all, of the symmetry elements are
- 3 different four-fold rotation axes (one through each pair of opposing faces of the visualized cube): up/down, in/out and left/right as seen in the photograph
- 4 different three-fold rotation axes (one through each pair of opposing corners of the cube [along each of the opposing arm/leg pairs])
- 6 different two-fold rotation axes (one through the midpoint of each opposing edge of the visualized cube)
- 9 mirror planes that bisect the visualized cube
- 3 that cut it top/bottom, left/right and front/back. These mirrors represent its reflective dihedral subsymmetry D2h, order 8 (a subordinate symmetry of any object with octahedral symmetry)
- 6 that go along the diagonals of opposing faces of the visualized cube (these go along double sets of arm-leg pairs). These mirrors represent its reflective tetrahedral subsymmetry Td, order 24 (a subordinate symmetry of any object with octahedral symmetry).
Using the mid room points, the sculpture represents the root systems of type D4, B4=C4 and F4, that is all 4d ones other than A4. It can visualize the projection of D4 to B3 and D4 to G2.
Science allusions
Many molecules have the same symmetry as the Octacube sculpture. The organic molecule, cubane (C8H8) is one example. The arms and legs of the sculpture are similar to the outward projecting hydrogen atoms. Sulfur hexafluoride (or any molecule with exact octahedral molecular geometry) also shares the same symmetry although the resemblance is not as similar.
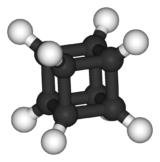
|
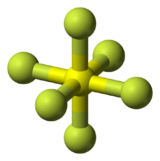
|
| Cubane | Sulfur hexafluoride |
The Octacube also shows parallels to concepts in theoretical physics. Creator Ocneanu researches mathematical aspects of quantum field theory (QFT). The subject has been described by a Fields medal winner, Ed Witten, as the most difficult area in physics.[2] Part of Ocneanu's work is to build theoretical, and even physical, models of the symmetry features in QFT. Ocneanu cites the relationship of the inner and outer halves of the structure as analogous to the relationship of spin 1/2 particles (e.g. electrons) and spin 1 particles (e.g. photons).[1]
Memorial
Octacube was commissioned and funded by Jill Anderson, a 1965 PSU math grad, in memory of her husband, Kermit, another 1965 math grad, who was killed in the 9-11 terrorist attacks.[1] Summarizing the memorial, Anderson said:[1]
I hope that the sculpture will encourage students, faculty, administrators, alumnae, and friends to ponder and appreciate the wonderful world of mathematics. I also hope that all who view the sculpture will begin to grasp the sobering fact that everyone is vulnerable to something terrible happening to them and that we all must learn to live one day at a time, making the very best of what has been given to us. It would be great if everyone who views the Octacube walks away with the feeling that being kind to others is a good way to live.
Anderson also funded a math scholarship in Kermit's name, at the same time the sculpture project went forward.[1]
Reception
A more complete explanation of the sculpture, including how it came to be made, how its construction was funded and its role in mathematics and physics, has been made available by Penn State.[1] In addition, Ocneanu has provided his own commentary.[3]
See also
Artists:
- Salvador Dalí, painter of fourth dimension allusions
- David Smith, a sculptor of abstract, geometric stainless steel
- Tony Smith, another creator of large abstract geometric sculptures
Math:
- Group theory, the mathematical discipline that historically encompassed much research into symmetry
- Operator algebra and Representation theory, Ocneanu's areas of math research
References
Notes
- ↑ The 4-D analog of the cube is the 8-celled tesseract. (In a similar manner, the 3-D analog of the square is the cube.) The 4-D analog of the octahedron is the 16-celled hexadecachoron. There is no regular polyhedron (Platonic solid) whose 4-D analog is the octacube (24-cell), but the 4-D analog of the quasi-regular cuboctahedron (Archimedean solid) is the octacube (24-cell).
Citations
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 News bulletin on the Octacube, Department of Mathematics, Penn State University, 13 October 2005 (accessed 2013-05-06)
- ↑ "Beautiful Minds, Vol. 20: Ed Witten". la Repubblica. 2010. http://temi.repubblica.it/iniziative-beautifulminds/. Here.
- ↑ The mathematics of the 24-cell, a website maintained by Adrian Ocneanu.
External links
- Video from Penn State about the Octacube
- User created video on imagining a four dimensional object (but a tesseract). Note discussion of projections at ~22 minutes and the discussion of the cells in the model at ~35 minutes.
[ ⚑ ] 40°47′51.5″N 77°51′43.7″W / 40.797639°N 77.862139°W
 |







