Direction cosine

Short description: Cosines of the angles between a vector and the coordinate axes

In analytic geometry, the direction cosines (or directional cosines) of a vector are the cosines of the angles between the vector and the three positive coordinate axes. Equivalently, they are the contributions of each component of the basis to a unit vector in that direction.

Three-dimensional Cartesian coordinates

Vector v in ${\mathbb{ℝ}}^3$

Direction cosines and direction angles for the unit vector $\frac{\mathbf{𝐯}}{|\mathbf{𝐯}|}$

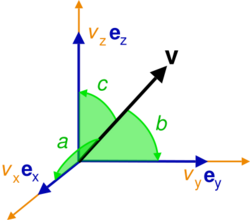
If v is a Euclidean vector in three-dimensional Euclidean space, ${\mathbb{ℝ}}^3,$

$$\mathbf{𝐯}=v_x{\mathbf{𝐞}}_x+v_y{\mathbf{𝐞}}_y+v_z{\mathbf{𝐞}}_z,$$

where e_x, e_y, e_z are the standard basis in Cartesian notation, then the direction cosines are

$$\begin{array}{rlrl}\alpha & =\cos a=\frac{\mathbf{𝐯}\cdot {\mathbf{𝐞}}_x}{\Vert \mathbf{𝐯}\Vert }& & =\frac{v_x}{\sqrt{v_x^2+v_y^2+v_z^2}},\\ \beta & =\cos b=\frac{\mathbf{𝐯}\cdot {\mathbf{𝐞}}_y}{\Vert \mathbf{𝐯}\Vert }& & =\frac{v_y}{\sqrt{v_x^2+v_y^2+v_z^2}},\\ \gamma & =\cos c=\frac{\mathbf{𝐯}\cdot {\mathbf{𝐞}}_z}{\Vert \mathbf{𝐯}\Vert }& & =\frac{v_z}{\sqrt{v_x^2+v_y^2+v_z^2}}.\end{array}$$

It follows that by squaring each equation and adding the results

$${\cos }^{2}a+{\cos }^{2}b+{\cos }^{2}c={\alpha }^2+{\beta }^2+{\gamma }^2=1.$$

Here α, β, γ are the direction cosines and the Cartesian coordinates of the unit vector $\frac{\mathbf{𝐯}}{|\mathbf{𝐯}|},$ and a, b, c are the direction angles of the vector v.

The direction angles a, b, c are acute or obtuse angles, i.e., 0 ≤ a ≤ π, 0 ≤ b ≤ π and 0 ≤ c ≤ π, and they denote the angles formed between v and the unit basis vectors e_x, e_y, e_z.

General meaning

More generally, direction cosine refers to the cosine of the angle between any two vectors. They are useful for forming direction cosine matrices that express one set of orthonormal basis vectors in terms of another set, or for expressing a known vector in a different basis. Simply put, direction cosines provide an easy method of representing the direction of a vector in a Cartesian coordinate system.

Applications

Determining angles between two vectors

Let u and v have direction cosines (α_u, β_u, γ_u) and (α_v, β_v, γ_v), respectively, having an angle θ between them. Their unit vectors are$$\begin{array}{rl}\hat{\mathbf{u}}& =\frac{u_x}{\Vert \mathbf{𝐮}\Vert }{\mathbf{𝐞}}_x+\frac{u_y}{\Vert \mathbf{𝐮}\Vert }{\mathbf{𝐞}}_y+\frac{u_z}{\Vert \mathbf{𝐮}\Vert }{\mathbf{𝐞}}_z={\alpha }_u{\mathbf{𝐞}}_x+{\beta }_u{\mathbf{𝐞}}_y+{\gamma }_u{\mathbf{𝐞}}_z\\ \hat{\mathbf{v}}& =\frac{v_x}{\Vert \mathbf{𝐯}\Vert }{\mathbf{𝐞}}_x+\frac{v_y}{\Vert \mathbf{𝐯}\Vert }{\mathbf{𝐞}}_y+\frac{v_z}{\Vert \mathbf{𝐯}\Vert }{\mathbf{𝐞}}_z={\alpha }_v{\mathbf{𝐞}}_x+{\beta }_v{\mathbf{𝐞}}_y+{\gamma }_v{\mathbf{𝐞}}_z\\ \end{array}$$respectively.

Taking the scalar product of these two unit vectors yield,$$\hat{\mathbf{u}}\mathbf{\cdot }\hat{\mathbf{v}}={\alpha }_u{\alpha }_v+{\beta }_u{\beta }_v+{\gamma }_u{\gamma }_v.$$The geometric interpretation of the scalar product of these two unit vectors is equivalent to the projection of one vector onto another; linking the two definitions we find the following.

${\alpha }_u{\alpha }_v+{\beta }_u{\beta }_v+{\gamma }_u{\gamma }_v=\cos \theta$

There exist two choices for θ (because cosine is odd); one is acute, another is the obtuse angle between them. The convention is to choose the acute, so we take the absolute value of the scalar product.$$\theta =\arccos \left(|{\alpha }_u{\alpha }_v+{\beta }_u{\beta }_v+{\gamma }_u{\gamma }_v|\right).$$

See also

• Cartesian tensor
• Euler angles

References

• Kay, D. C. (1988). Tensor Calculus. Schaum’s Outlines. McGraw Hill. pp. 18–19. ISBN 0-07-033484-6. 
• Spiegel, M. R.; Lipschutz, S.; Spellman, D. (2009). Vector analysis. Schaum’s Outlines (2nd ed.). McGraw Hill. pp. 15, 25. ISBN 978-0-07-161545-7. 
• Tyldesley, J. R. (1975). An introduction to tensor analysis for engineers and applied scientists. Longman. p. 5. ISBN 0-582-44355-5. https://books.google.com/books?id=PODXAAAAMAAJ. 
• Tang, K. T. (2006). Mathematical Methods for Engineers and Scientists. 2. Springer. p. 13. ISBN 3-540-30268-9.