Earth:Soil consolidation

Two oedometers at the University of Cambridge

Soil consolidation refers to the mechanical process by which soil changes volume gradually in response to a change in pressure. This happens because soil is a two-phase material, comprising soil grains and pore fluid, usually groundwater. When soil saturated with water is subjected to an increase in pressure, the high volumetric stiffness of water compared to the soil matrix means that the water initially absorbs all the change in pressure without changing volume, creating excess pore water pressure. As water diffuses away from regions of high pressure due to seepage, the soil matrix gradually takes up the pressure change and shrinks in volume. The theoretical framework of consolidation is therefore closely related to the concept of effective stress, and hydraulic conductivity. The early theoretical modern models were proposed one century ago, according to two different approaches, by Karl Terzaghi and Paul Fillunger. The Terzaghi’s model is currently the most utilized in engineering practice and is based on the diffusion equation.

In the narrow sense, "consolidation" refers strictly to this delayed volumetric response to pressure change due to gradual movement of water. Some publications also use "consolidation" in the broad sense, to refer to any process by which soil changes volume due to a change in applied pressure. This broader definition encompasses the overall concept of soil compaction, subsidence, and heave. Some types of soil, mainly those rich in organic matter, show significant creep, whereby the soil changes volume slowly at constant effective stress over a longer time-scale than consolidation due to the diffusion of water. To distinguish between the two mechanisms, "primary consolidation" refers to consolidation due to dissipation of excess water pressure, while "secondary consolidation" refers to the creep process.

The effects of consolidation are most conspicuous where a building sits over a layer of soil with low stiffness and low permeability, such as marine clay, leading to large settlement over many years. Types of construction project where consolidation often poses technical risk include land reclamation, the construction of embankments, and tunnel and basement excavation in clay.

Geotechnical engineers use oedometers to quantify the effects of consolidation. In an oedometer test, a series of known pressures are applied to a thin disc of soil sample, and the change of sample thickness with time is recorded. This allows the consolidation characteristics of the soil to be quantified in terms of the coefficient of consolidation ([math]\displaystyle{ C_{v} }[/math]) and hydraulic conductivity ([math]\displaystyle{ K }[/math]).

Clays undergo consolidation settlement not only by the action of external loads (surcharge loads) but also under its own weight or weight of soils that exist above the clay.

Clays also undergo settlement when dewatered (groundwater pumping) because the effective stress on the clay increases.

Coarse-grained soils do not undergo consolidation settlement due to relatively high hydraulic conductivity compared to clays. Instead, Coarse-grained soils undergo the immediate settlement.

History and terminology

The first modern theoretical models for soil consolidation were proposed in the 1920s by Terzaghi and Fillunger, according to two substantially different approaches. The former was based on diffusion equations in eulerian notation, whereas the latter considered the local Newton’s law for both liquid and solid phases, in which main variables, such as partial pressure, porosity, local velocity etc., were involved by means of the mixture theory. Terzaghi had an engineering approach to the problem of soil consolidation and provided simplified models that are still widely used in engineering practice today, whereas, on the other hand, Fillunger had a rigorous approach to the above problems and provided rigorous mathematical models that paid particular attention to the methods of local averaging of the involved variables. Fillunger’s model was very abstract and involved variables that were difficult to detect experimentally, and, therefore, it was not applicable to the study of real cases by engineers and/or designers. Nevertheless, this provided the basis for advanced theoretical studies of particularly complex problems. Due to the different approach to the problem of consolidation by the two scientists, a bitter scientific dispute arose between them, and this unfortunately led to a tragic ending in 1937. After Fillunger’s suicide, his theoretical results were forgotten for decades, whereas the methods proposed by Terzaghi found widespread diffusion among scientists and professionals. In the following decades Biot fully developed the three-dimensional soil consolidation theory, extending the one-dimensional model previously proposed by Terzaghi to more general hypotheses and introducing the set of basic equations of poroelasticity. Today, the Terzaghis’ one dimensional model is still the most utilized by engineers for its conceptual simplicity and because it is based on experimental data, such as oedometer tests, which are relatively simple, reliable and inexpensive and for which theoretical solutions in closed form are well known. According to the "father of soil mechanics", Karl von Terzaghi, consolidation is "any process which involves a decrease in water content of saturated soil without replacement of water by air". More generally, consolidation refers to the process by which soils change volume in response to a change in pressure, encompassing both compaction and swelling.

Magnitude of volume change

The experimentally determined consolidation curve (blue dots) for a saturated clay showing a procedure for computing the preconsolidation stress.

Construction of compression and recompression curve. The curve, generally referred to as the virgin compression curve, approximately intersects the laboratory curve at a void ratio of 0.42[math]\displaystyle{ e_0 }[/math] (Terzaghi and Peck, 1967). Note that [math]\displaystyle{ e_0 }[/math] is the void ratio of the clay in the field. Knowing the values of [math]\displaystyle{ e_0 }[/math] and [math]\displaystyle{ \sigma^'_c }[/math] you can easily construct the virgin curve and calculate its compression index by using Eq. [math]\displaystyle{ C_C=\frac{e_1-e_2}{log(\frac{\sigma^'_2}{\sigma^'_1})} }[/math].

Consolidation is the process in which reduction in volume takes place by the gradual expulsion or absorption of water under long-term static loads.

When stress is applied to a soil, it causes the soil particles to pack together more tightly. When this occurs in a soil that is saturated with water, water will be squeezed out of the soil. The magnitude of consolidation can be predicted by many different methods. In the classical method developed by Terzaghi, soils are tested with an oedometer test to determine their compressibility. In most theoretical formulations, a logarithmic relationship is assumed between the volume of the soil sample and the effective stress carried by the soil particles. The constant of proportionality (change in void ratio per order of magnitude change in effective stress) is known as the compression index, given the symbol [math]\displaystyle{ \lambda }[/math] when calculated in natural logarithm and [math]\displaystyle{ C_C }[/math] when calculated in base-10 logarithm.

This can be expressed in the following equation, which is used to estimate the volume change of a soil layer:

[math]\displaystyle{ \delta_c = \frac{ C_c }{ 1 + e_0 } H \log \left( \frac{ \sigma_{zf}' }{ \sigma_{z0}' } \right) \ }[/math]

where

δ_c is the settlement due to consolidation.

C_c is the compression index.

e₀ is the initial void ratio.

H is the height of the compressible soil.

σ_zf is the final vertical stress.

σ_z0 is the initial vertical stress.

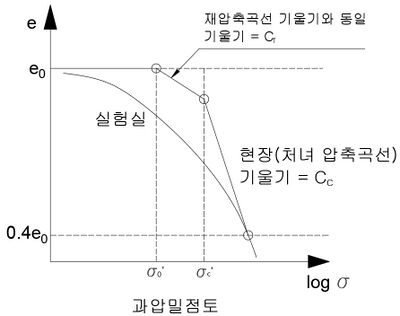
When stress is removed from a consolidated soil, the soil will rebound, regaining some of the volume it had lost in the consolidation process. If the stress is reapplied, the soil will consolidate again along a recompression curve, defined by the recompression index. The gradient of the swelling and recompression lines on a plot of void ratio against the logarithm of effective stress often idealised to take the same value, known as the "swelling index" (given the symbol [math]\displaystyle{ \kappa }[/math] when calculated in natural logarithm and [math]\displaystyle{ C_S }[/math] when calculated in base-10 logarithm).

C_c can be replaced by C_r (the recompression index) for use in overconsolidated soils where the final effective stress is less than the preconsolidation stress. When the final effective stress is greater than the preconsolidation stress, the two equations must be used in combination to model both the recompression portion and the virgin compression portion of the consolidation processes, as follows,

[math]\displaystyle{ \delta_c = \frac{ C_r }{ 1 + e_0 } H \log \left( \frac{ \sigma_{zc}' }{ \sigma_{z0}' } \right) + \frac{ C_c }{ 1 + e_0 } H \log \left( \frac{ \sigma_{zf}' }{ \sigma_{zc}' } \right)\ }[/math]

where σ_zc is the preconsolidation stress of the soil.

This method assumes consolidation occurs in only one-dimension. Laboratory data is used to construct a plot of strain or void ratio versus effective stress where the effective stress axis is on a logarithmic scale. The plot's slope is the compression index or recompression index. The equation for consolidation settlement of a normally consolidated soil can then be determined to be:

The soil which had its load removed is considered to be "overconsolidated". This is the case for soils that have previously had glaciers on them. The highest stress that it has been subjected to is termed the "preconsolidation stress". The "over-consolidation ratio" (OCR) is defined as the highest stress experienced divided by the current stress. A soil that is currently experiencing its highest stress is said to be "normally consolidated" and has an OCR of one. A soil could be considered "underconsolidated" or "unconsolidated" immediately after a new load is applied but before the excess pore water pressure has dissipated. Occasionally, soil strata form by natural deposition in rivers and seas may exist in an exceptionally low density that is impossible to achieve in an oedometer; this process is known as "intrinsic consolidation".

Time dependency

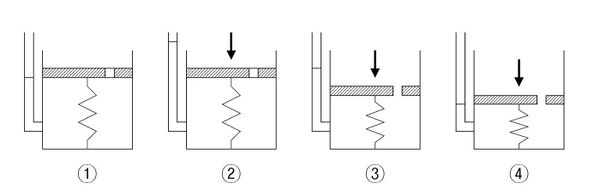
Spring analogy

The process of consolidation is often explained with an idealized system composed of a spring, a container with a hole in its cover, and water. In this system, the spring represents the compressibility or the structure of the soil itself, and the water which fills the container represents the pore water in the soil.

Schematic diagram of spring analogy

1. The container is completely filled with water, and the hole is closed. (Fully saturated soil)
2. A load is applied onto the cover, while the hole is still unopened. At this stage, only the water resists the applied load. (Development of excess pore water pressure)
3. As soon as the hole is opened, water starts to drain out through the hole and the spring shortens. (Drainage of excess pore water pressure)
4. After some time, the drainage of water no longer occurs. Now, the spring alone resists the applied load. (Full dissipation of excess pore water pressure. End of consolidation)

Analytical formulation of consolidation rate

The time for consolidation to occur can be predicted. Sometimes consolidation can take years. This is especially true in saturated clays because their hydraulic conductivity is extremely low, and this causes the water to take an exceptionally long time to drain out of the soil. While drainage is occurring, the pore water pressure is greater than normal because it is carrying part of the applied stress (as opposed to the soil particles).

[math]\displaystyle{ T_v=\frac{c_v*t}{(H_{dr})^2} \ }[/math]

Where T_v is the time factor.

H_dr is the average longest drain path during consolidation.

t is the time at measurement

C_v is defined as the coefficient of consolidation found using the log method with

[math]\displaystyle{ C_v=\frac{T_{50}H_{dr}^2}{t_{50}} }[/math]

or the root method with

[math]\displaystyle{ C_v=\frac{T_{95}H_{dr}^2}{t_{95}} }[/math]

t₅₀ time to 50% deformation (consolidation) and t₉₅ is 95%

Where T₉₅=1.129 T₅₀=0.197

Creep

The theoretical formulation above assumes that time-dependent volume change of a soil unit only depends on changes in effective stress due to the gradual restoration of steady-state pore water pressure. This is the case for most types of sand and clay with low amounts of organic material. However, in soils with a high amount of organic material such as peat, the phenomenon of creep also occurs, whereby the soil changes volume gradually at constant effective stress. Soil creep is typically caused by viscous behavior of the clay-water system and compression of organic matter.

This process of creep is sometimes known as "secondary consolidation" or "secondary compression" because it also involves gradual change of soil volume in response to an application of load; the designation "secondary" distinguishes it from "primary consolidation", which refers to volume change due to dissipation of excess pore water pressure. Creep typically takes place over a longer time-scale than (primary) consolidation, such that even after the restoration of hydrostatic pressure some compression of soil takes place at slow rate.

Analytically, the rate of creep is assumed to decay exponentially with time since application of load, giving the formula:

[math]\displaystyle{ S_s=\frac{H_0}{1+e_0} C_{a} \log \left( \frac {t} {t_{95} } \right) \ }[/math]

Where H₀ is the height of the consolidating medium
e₀ is the initial void ratio
C_a is the secondary compression index
t is the length of time after consolidation considered
t₉₅ is the length of time for achieving 95% consolidation

Deformation characteristics of consolidation

Coefficient of compressibility [math]\displaystyle{ a_v = \frac{ \Delta e}{ \Delta \sigma_'} }[/math]. The compressibility of saturated specimens of clay minerals increases in the order kaolinite <illite<smectite. The compression index Cc, which is defined as the change in void ratio per 10-fold increase in consolidation pressure, is in the range of 0.19 to 0.28 for kaolinite, 0.50 to 1.10 for illite, and 1.0 to 2.6 for montmorillonite, for different ionic forms. The more compressible the clay, the more pronounced the influences of cation type and electrolyte concentration on compressibility.

Coefficient of volume compressibility [math]\displaystyle{ m_v = \frac{ \Delta V / V}{ \Delta \sigma_'}=\frac{a_v}{ \Delta \sigma_'} }[/math]

See also

• Compaction (geology)
• Settlement (structural)
• Soil mechanics
• Vacuum consolidation

Bibliography

• Coduto, Donald (2001), Foundation Design, Prentice-Hall, ISBN 0-13-589706-8 
• Kim, Myung-mo (2000) (in ko), Soil Mechanics (4 ed.), Seoul: Munundang, ISBN 89-7393-053-2 
• Terzaghi, Karl (1943), Theoretical soil mechanics, John Wiley&Sons, Inc., p. 265