Epispiral

Short description: Type of plane curve

An epispiral with equation r(θ)=2sec(2θ)

The epispiral is a plane curve with polar equation

[math]\displaystyle{ \ r=a \sec{n\theta} }[/math].

There are n sections if n is odd and 2n if n is even.

It is the polar or circle inversion of the rose curve.

In astronomy the epispiral is related to the equations that explain planets' orbits.

Alternative definition

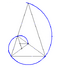
There is another definition of the epispiral that has to do with tangents to circles:

Begin with a circle.

Rotate some single point on the circle around the circle by some angle [math]\displaystyle{ \theta }[/math] and at the same time by an angle in constant proportion to [math]\displaystyle{ \theta }[/math], say [math]\displaystyle{ c\theta }[/math] for some constant [math]\displaystyle{ c }[/math].

The intersections of the tangent lines to the circle at these new points rotated from that single point for every [math]\displaystyle{ \theta }[/math] would trace out an epispiral.

The polar equation can be derived through simple geometry as follows:

To determine the polar coordinates [math]\displaystyle{ (\rho,\phi) }[/math] of the intersection of the tangent lines in question for some [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ -1\lt c\lt 1 }[/math], note that [math]\displaystyle{ \phi }[/math] is halfway between [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ c\theta }[/math] by congruence of triangles, so it is [math]\displaystyle{ \frac{(c+1)\theta}{2} }[/math]. Moreover, if the radius of the circle generating the curve is [math]\displaystyle{ r }[/math], then since there is a right-angled triangle (it's right-angled as a tangent to a circle meets the radius at a right angle at the point of tangency) with hypotenuse [math]\displaystyle{ \rho }[/math] and an angle [math]\displaystyle{ \frac{(1-c) \theta}{2} }[/math] to which the adjacent leg of the triangle is [math]\displaystyle{ r }[/math], the radius [math]\displaystyle{ \rho }[/math] at the intersection point of the relevant tangents is [math]\displaystyle{ r\sec(\frac{(1-c)\theta}{2}) }[/math]. This gives the polar equation of the curve, [math]\displaystyle{ \rho=r\sec(\frac{(1-c)\phi}{c+1}) }[/math] for all points [math]\displaystyle{ (\rho,\phi) }[/math] on it.

See also

• Logarithmic spiral
• Rose (mathematics)

References

• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. p. 192. ISBN 0-486-60288-5. https://archive.org/details/catalogofspecial00lawr/page/192. 
• https://www.mathcurve.com/courbes2d.gb/epi/epi.shtml