List of spirals

Short description: none

This list is incomplete; you can help by expanding it.

This list of spirals includes named spirals that have been described mathematically.

Image	Name	First described	Equation	Comment
	Circle		$r=k$	The trivial spiral
	Archimedean spiral (also arithmetic spiral)	-300 c. 320 BC	$r=a+b\cdot \theta$
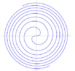	Fermat's spiral (also parabolic spiral)	1636	$r^2=a^2\cdot \theta$	Encloses equal area per turn
	Doyle spiral	1980—1990		circle packing, using circles of structured radii
	Euler spiral (also Cornu spiral or polynomial spiral)	1696	$x(t)=\mathrm{C}(t),$$y(t)=\mathrm{S}(t)$	Using Fresnel integrals
	Hyperbolic spiral (also reciprocal spiral)	1704	$r=\frac{a}{\theta }$
	Lituus	1722	$r^2\cdot \theta =k$
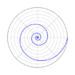	Logarithmic spiral (also known as equiangular spiral)	1638	$r=a\cdot e^{b\cdot \theta }$	Constant pitch angle. Approximations of this are found in nature
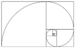
	Fibonacci spiral		Circular arcs connecting the opposite corners of squares in the Fibonacci tiling	Approximation of the golden spiral
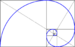
	Golden spiral		$r={\phi }^{\frac{2\cdot \theta }{\pi }}$	Special case of the logarithmic spiral
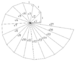	Spiral of Theodorus (also known as Pythagorean spiral)	-500 c. 500 BC	Contiguous right triangles composed of one leg with unit length and the other leg being the hypotenuse of the prior triangle	Approximates the Archimedean spiral
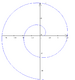	Involute	1673	$x(t)=r(\cos (t+a)+t\sin (t+a)),$ $y(t)=r(\sin (t+a)-t\cos (t+a))$	Involutes of a circle appear like Archimedean spirals
	Helix		$r(t)=1,$ $\theta (t)=t,$ $z(t)=t$	A three-dimensional spiral
	Rhumb line (also loxodrome)			Type of spiral drawn on a sphere
	Cotes's spiral	1722	$\frac{1}{r}=\{\begin{array}{l}A\cosh (k\theta +\epsilon )\\ A\exp (k\theta +\epsilon )\\ A\sinh (k\theta +\epsilon )\\ A(k\theta +\epsilon )\\ A\cos (k\theta +\epsilon )\\ \end{array}$	Solution to the two-body problem for an inverse-cube central force
	Poinsot's spirals		$r=a\cdot \mathrm{csch}(n\cdot \theta ),$ $r=a\cdot \mathrm{sech}(n\cdot \theta )$
	Nielsen's spiral	1993	$x(t)=\mathrm{ci}(t),$ $y(t)=\mathrm{si}(t)$	A variation of Euler spiral, using sine integral and cosine integrals
	Polygonal spiral			Special case approximation of arithmetic or logarithmic spiral
	Fraser's Spiral	1908		Optical illusion based on spirals
	Conchospiral		$r={\mu }^t\cdot a,$$\theta =t,$$z={\mu }^t\cdot c$	A three-dimensional spiral on the surface of a cone.
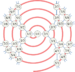	Calkin–Wilf spiral
	Ulam spiral (also prime spiral)	1963
	Sacks spiral	1994		Variant of Ulam spiral and Archimedean spiral.
	Seiffert's spiral	2000	$r=\mathrm{sn}(s,k),$$\theta =k\cdot s$$z=\mathrm{cn}(s,k)$	Spiral curve on the surface of a sphere using the Jacobi elliptic functions
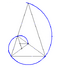
	Tractrix spiral	1704	$\{\begin{array}{l}r=A\cos (t)\\ \theta =\tan (t)-t\end{array}$
	Pappus spiral	1779	$\{\begin{array}{l}r=a\theta \\ \psi =k\end{array}$	3D conical spiral studied by Pappus and Pascal
	Doppler spiral		$x=a\cdot (t\cdot \cos (t)+k\cdot t),$$y=a\cdot t\cdot \sin (t)$	2D projection of Pappus spiral
	Atzema spiral		$x=\frac{\sin (t)}{t}-2\cdot \cos (t)-t\cdot \sin (t),$$y=-\frac{\cos (t)}{t}-2\cdot \sin (t)+t\cdot \cos (t)$	The curve that has a catacaustic forming a circle. Approximates the Archimedean spiral.
	Atomic spiral	2002	$r=\frac{\theta }{\theta -a}$	This spiral has two asymptotes; one is the circle of radius 1 and the other is the line $\theta =a$
	Galactic spiral	2019	$\{\begin{array}{l}dx=R\cdot \frac{y}{\sqrt{x^2+y^2}}d\theta \\ dy=R\cdot [\rho (\theta )-\frac{x}{\sqrt{x^2+y^2}}]d\theta \end{array}\{\begin{array}{l}x=\sum dx\\ \\ \\ y=\sum dy+R\end{array}$	The differential spiral equations were developed to simulate the spiral arms of disc galaxies, have 4 solutions with three different cases:$\rho <1,\rho =1,\rho >1$, the spiral patterns are decided by the behavior of the parameter $\rho$. For $\rho <1$, spiral-ring pattern; $\rho =1,$ regular spiral; $\rho >1,$ loose spiral. R is the distance of spiral starting point (0, R) to the center. The calculated x and y have to be rotated backward by ($-\theta$) for plotting.Template:Pred

See also

• Catherine wheel (firework)
• List of spiral galaxies
• Parker spiral
• Spirangle
• Spirograph