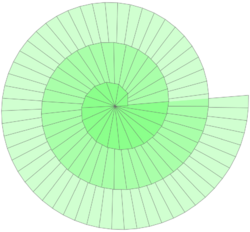
Spiral of Theodorus

Short description: Polygonal curve made from right triangles

The spiral of Theodorus up to the triangle with a hypotenuse of [math]\displaystyle{ \sqrt{17} }[/math]

In geometry, the spiral of Theodorus (also called the square root spiral, Pythagorean spiral, or Pythagoras's snail) is a spiral composed of right triangles, placed edge-to-edge. It was named after Theodorus of Cyrene.

Construction

The spiral is started with an isosceles right triangle, with each leg having unit length. Another right triangle is formed, an automedian right triangle with one leg being the hypotenuse of the prior triangle (with length the square root of 2) and the other leg having length of 1; the length of the hypotenuse of this second triangle is the square root of 3. The process then repeats; the [math]\displaystyle{ n }[/math]th triangle in the sequence is a right triangle with the side lengths [math]\displaystyle{ \sqrt{n} }[/math] and 1, and with hypotenuse [math]\displaystyle{ \sqrt{n+1} }[/math]. For example, the 16th triangle has sides measuring [math]\displaystyle{ 4=\sqrt{16} }[/math], 1 and hypotenuse of [math]\displaystyle{ \sqrt{17} }[/math].

History and uses

Although all of Theodorus' work has been lost, Plato put Theodorus into his dialogue Theaetetus, which tells of his work. It is assumed that Theodorus had proved that all of the square roots of non-square integers from 3 to 17 are irrational by means of the Spiral of Theodorus.

Plato does not attribute the irrationality of the square root of 2 to Theodorus, because it was well known before him. Theodorus and Theaetetus split the rational numbers and irrational numbers into different categories.

Hypotenuse

Each of the triangles' hypotenuses [math]\displaystyle{ h_n }[/math] gives the square root of the corresponding natural number, with [math]\displaystyle{ h_1=\sqrt{2} }[/math].

Plato, tutored by Theodorus, questioned why Theodorus stopped at [math]\displaystyle{ \sqrt{17} }[/math]. The reason is commonly believed to be that the [math]\displaystyle{ \sqrt{17} }[/math] hypotenuse belongs to the last triangle that does not overlap the figure.

Overlapping

In 1958, Kaleb Williams proved that no two hypotenuses will ever coincide, regardless of how far the spiral is continued. Also, if the sides of unit length are extended into a line, they will never pass through any of the other vertices of the total figure.

Extension

Colored extended spiral of Theodorus with 110 triangles

Theodorus stopped his spiral at the triangle with a hypotenuse of [math]\displaystyle{ \sqrt{17} }[/math]. If the spiral is continued to infinitely many triangles, many more interesting characteristics are found.

Growth rate

Angle

If [math]\displaystyle{ \varphi_n }[/math] is the angle of the [math]\displaystyle{ n }[/math]th triangle (or spiral segment), then: [math]\displaystyle{ \tan\left(\varphi_n\right)=\frac{1}{\sqrt{n}}. }[/math] Therefore, the growth of the angle [math]\displaystyle{ \varphi_n }[/math] of the next triangle [math]\displaystyle{ n }[/math] is: [math]\displaystyle{ \varphi_n=\arctan\left(\frac{1}{\sqrt{n}}\right). }[/math]

The sum of the angles of the first [math]\displaystyle{ k }[/math] triangles is called the total angle [math]\displaystyle{ \varphi(k) }[/math] for the [math]\displaystyle{ k }[/math]th triangle. It grows proportionally to the square root of [math]\displaystyle{ k }[/math], with a bounded correction term [math]\displaystyle{ c_2 }[/math]: [math]\displaystyle{ \varphi\left (k\right)=\sum_{n=1}^k\varphi_n = 2\sqrt{k}+c_2(k) }[/math] where [math]\displaystyle{ \lim_{k \to \infty} c_2(k)= - 2.157782996659\ldots }[/math] (OEIS: A105459).

A triangle or section of spiral

Radius

The growth of the radius of the spiral at a certain triangle [math]\displaystyle{ n }[/math] is [math]\displaystyle{ \Delta r=\sqrt{n+1}-\sqrt{n}. }[/math]

Archimedean spiral

The Spiral of Theodorus approximates the Archimedean spiral. Just as the distance between two windings of the Archimedean spiral equals mathematical constant [math]\displaystyle{ \pi }[/math], as the number of spins of the spiral of Theodorus approaches infinity, the distance between two consecutive windings quickly approaches [math]\displaystyle{ \pi }[/math].

The following table shows successive windings of the spiral approaching pi:

Winding No.:	Calculated average winding-distance	Accuracy of average winding-distance in comparison to π
2	3.1592037	99.44255%
3	3.1443455	99.91245%
4	3.14428	99.91453%
5	3.142395	99.97447%
[math]\displaystyle{ \to\infty }[/math]	[math]\displaystyle{ \to\pi }[/math]	[math]\displaystyle{ \to 100\% }[/math]

As shown, after only the fifth winding, the distance is a 99.97% accurate approximation to [math]\displaystyle{ \pi }[/math].

Continuous curve

Davis' analytic continuation of the Spiral of Theodorus, including extension in the opposite direction from the origin (negative nodes numbers).

The question of how to interpolate the discrete points of the spiral of Theodorus by a smooth curve was proposed and answered in (Davis 2001) by analogy with Euler's formula for the gamma function as an interpolant for the factorial function. Davis found the function [math]\displaystyle{ T(x) = \prod_{k=1}^\infty \frac{1 + i/\sqrt{k}}{1 + i/\sqrt{x+k}} \qquad ( -1 \lt x \lt \infty ) }[/math] which was further studied by his student Leader and by Iserles (in an appendix to (Davis 2001) ). An axiomatic characterization of this function is given in (Gronau 2004) as the unique function that satisfies the functional equation [math]\displaystyle{ f(x+1) = \left( 1 + \frac{i}{\sqrt{x+1} }\right) \cdot f(x), }[/math] the initial condition [math]\displaystyle{ f(0) = 1, }[/math] and monotonicity in both argument and modulus; alternative conditions and weakenings are also studied therein. An alternative derivation is given in ( Heuvers Moak ).

An analytic continuation of Davis' continuous form of the Spiral of Theodorus which extends in the opposite direction from the origin is given in (Waldvogel 2009).

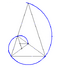
In the figure the nodes of the original (discrete) Theodorus spiral are shown as small green circles. The blue ones are those, added in the opposite direction of the spiral. Only nodes [math]\displaystyle{ n }[/math] with the integer value of the polar radius [math]\displaystyle{ r_n=\pm\sqrt{|n|} }[/math] are numbered in the figure. The dashed circle in the coordinate origin [math]\displaystyle{ O }[/math] is the circle of curvature at [math]\displaystyle{ O }[/math].

See also

• Fermat's spiral
• List of spirals

Further reading

• Davis, P. J. (2001), Spirals from Theodorus to Chaos, A K Peters/CRC Press 
• Gronau, Detlef (March 2004), "The Spiral of Theodorus", The American Mathematical Monthly 111 (3): 230–237, doi:10.2307/4145130 
• Heuvers, J.; Moak, D. S.; Boursaw, B (2000), "The functional equation of the square root spiral", in T. M. Rassias, Functional Equations and Inequalities, pp. 111–117 
• Waldvogel, Jörg (2009), Analytic Continuation of the Theodorus Spiral, http://www.math.ethz.ch/~waldvoge/Papers/theopaper.pdf