Fourier ptychography
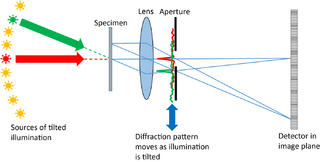
Fourier ptychography is a computational imaging technique based on optical microscopy that consists in the synthesis of a wider numerical aperture from a set of full-field images acquired at various coherent illumination angles,[1] resulting in increased resolution compared to a conventional microscope.
Each image is acquired under the illumination of a coherent light source at various angles of incidence (typically from an array of LEDs); the acquired image set is then combined using an iterative phase retrieval algorithm into a final high-resolution image that can contain up to a billion pixels (a gigapixel) with diffraction-limited resolution, resulting in a high space-bandwidth product.
Fourier ptychography reconstructs the complex image of the object (with quantitative phase information), but contrary to holography, it is a non-interferometric imaging technique and thus often easier to implement.
The name "ptychography" comes from the ancient Greek word πτυχή ("to fold", also found in the word triptych), because the technique is based on multiple "views" of the object.
Image reconstruction algorithms
The image reconstruction algorithms are based on iterative phase retrieval,[2] either related to the Gerchberg–Saxton algorithm or based on convex relaxation methods.[3] Like real space ptychography, the solution of the phase problem relies on the same mathematical shift invariance constraint, except in Fourier ptychography it is the diffraction pattern in the back focal plane that is moving with respect to the back-focal plane aperture. (In traditional ptychography the illumination moves with respect to the specimen.) Many reconstruction algorithms used in real-space ptychography are therefore used in Fourier ptychography, most commonly PIE[4][5] and variants such as ePIE[6] and 3PIE.[7] Variants of these algorithms allow for simultaneous reconstruction of the pupil function of an optical system,[8] allowing for the correction of the aberrations of the microscope objective, and diffraction tomography[9] which permits the 3D reconstruction of thin sample objects without requiring the angular sample scanning needed for CT scans.
Advantages
Fourier ptychography can be easily implemented on a conventional optical microscope by replacing the illumination source by an array of LED and improve the optical resolution by a factor 2 (with only bright-field illumination) or more (when including dark-field images to the reconstruction.)
A major advantage of Fourier ptychography is the ability to use a microscope objective with a lower numerical aperture without sacrificing the resolution. The use of a lower numerical aperture allows for larger field of view, larger depth of focus, and larger working distance. Moreover, it enables effective numerical aperture larger than 1 without resorting to oil immersion.[10]
Relation to ptychography
Contrary to Fourier ptychography, (conventional) ptychography swaps the role of the focus element, from an objective to become a condenser, and relies on the acquisition of diffractograms with illumination position diversity. However, the two techniques are both based on the determination of the angular spectrum of the object through a phase retrieval procedure,[11] and inherently reconstruct the same information. Therefore, Fourier ptychography and conventional ptychography provides a bridge between coherent diffraction imaging and full-field microscopy.
See also
References
- ↑ G. Zheng, R. Horstmeyer and C. Yang (2013). "Wide-field, high-resolution Fourier ptychographic microscopy". Nature Photonics 7 (9): 739–745. doi:10.1038/nphoton.2013.187. PMID 25243016. Bibcode: 2013NaPho...7..739Z.
- ↑ Yeh, Li-Hao; Dong, Jonathan; Zhong, Jingshan; Tian, Lei; Chen, Michael; Tang, Gongguo; Soltanolkotabi, Mahdi; Waller, Laura (2015). "Experimental robustness of Fourier ptychography phase retrieval algorithms". Optics Express 23 (26): 33214–40. doi:10.1364/OE.23.033214. PMID 26831989.
- ↑ Horstmeyer, Roarke; Chen, Richard Y.; Ou, Xiaoze; Ames, Brendan; Tropp, Joel A.; Yang, Changhuei (2015). "Solving ptychography with a convex relaxation". New Journal of Physics 17 (5): 053044. doi:10.1088/1367-2630/17/5/053044. PMID 26146480.
- ↑ Faulkner, H. M. L.; Rodenburg, J. M. (2004). "Movable Aperture Lensless Transmission Microscopy: A Novel Phase Retrieval Algorithm". Physical Review Letters 93 (2): 023903. doi:10.1103/PhysRevLett.93.023903. PMID 15323918.
- ↑ Rodenburg, J. M.; Faulkner, H. M. L. (2004). "A phase retrieval algorithm for shifting illumination" (in en). Applied Physics Letters 85 (20): 4795–4797. doi:10.1063/1.1823034. ISSN 0003-6951. Bibcode: 2004ApPhL..85.4795R.
- ↑ Maiden, Andrew M.; Rodenburg, John M. (2009). "An improved ptychographical phase retrieval algorithm for diffractive imaging". Ultramicroscopy 109 (10): 1256–1262. doi:10.1016/j.ultramic.2009.05.012. ISSN 0304-3991. PMID 19541420.
- ↑ Maiden, A. M.; Humphry, M. J.; Rodenburg, J. M. (2012). "Ptychographic transmission microscopy in three dimensions using a multi-slice approach" (in EN). JOSA A 29 (8): 1606–1614. doi:10.1364/JOSAA.29.001606. ISSN 1520-8532. PMID 23201876. Bibcode: 2012JOSAA..29.1606M.
- ↑ Ou, Xiaoze; Zheng, Guoan; Yang, Changhuei (2014). "Embedded pupil function recovery for Fourier ptychographic microscopy". Optics Express 22 (5): 4960–72. doi:10.1364/OE.22.004960. PMID 24663835.
- ↑ Horstmeyer (2016). "Diffraction tomography with Fourier ptychography". Optica 3 (8): 827–835. doi:10.1364/OPTICA.3.000827. PMID 28736737.
- ↑ Ou, Xiaoze; Horstmeyer, Roarke; Zheng, Guoan; Yang, Changhuei (2015). "High numerical aperture Fourier ptychography: Principle, implementation and characterization". Optics Express 23 (3): 3472–91. doi:10.1364/OE.23.003472. PMID 25836203.
- ↑ Horstmeyer (2014). "A phase space model of Fourier ptychographic microscopy Roarke". Optics Express 22 (1): 338–358. doi:10.1364/OE.22.000338. PMID 24514995.
 |
