Geodetic datum

Short description: Reference frame used in geodesy, surveying, chartography and navigation

A geodetic datum or geodetic system (also: geodetic reference datum or geodetic reference system) is a coordinate system, and a set of reference points, used for locating places on the Earth (or similar objects). An approximate definition of sea level is the datum WGS 84, an ellipsoid, whereas a more accurate definition is Earth Gravitational Model 2008 (EGM2008), using at least 2,159 spherical harmonics. Other datums are defined for other areas or at other times; ED50 was defined in 1950 over Europe and differs from WGS 84 by a few hundred meters depending on where in Europe you look. Mars has no oceans and so no sea level, but at least two martian datums have been used to locate places there.

Datums are used in geodesy, navigation, and surveying by cartographers and satellite navigation systems to translate positions indicated on maps (paper or digital) to their real position on Earth. Each starts with an ellipsoid (stretched sphere), and then defines latitude, longitude and altitude coordinates. One or more locations on the Earth's surface are chosen as anchor "base-points".

The difference in co-ordinates between datums is commonly referred to as datum shift. The datum shift between two particular datums can vary from one place to another within one country or region, and can be anything from zero to hundreds of meters (or several kilometers for some remote islands). The North Pole, South Pole and Equator will be in different positions on different datums, so True North will be slightly different. Different datums use different interpolations for the precise shape and size of the Earth (reference ellipsoids).

Because the Earth is an imperfect ellipsoid, localised datums can give a more accurate representation of the area of coverage than WGS 84. OSGB36, for example, is a better approximation to the geoid covering the British Isles than the global WGS 84 ellipsoid. However, as the benefits of a global system outweigh the greater accuracy, the global WGS 84 datum is becoming increasingly adopted.

Horizontal datums are used for describing a point on the Earth's surface, in latitude and longitude or another coordinate system. Vertical datums measure elevations or depths.

City of Chicago Datum Benchmark

Definition

In surveying and geodesy, a datum is a reference system or an approximation of the Earth's surface against which positional measurements are made for computing locations. Horizontal datums are used for describing a point on the Earth's surface, in latitude and longitude or another coordinate system. Vertical datums are used to measure elevations or underwater depths.

Horizontal datum

The horizontal datum is the model used to measure positions on the Earth. A specific point on the Earth can have substantially different coordinates, depending on the datum used to make the measurement. There are hundreds of local horizontal datums around the world, usually referenced to some convenient local reference point. Contemporary datums, based on increasingly accurate measurements of the shape of the Earth, are intended to cover larger areas. The WGS 84 datum, which is almost identical to the NAD83 datum used in North America and the ETRS89 datum used in Europe, is a common standard datum.

For example, in Sydney there is a 200 metres (700 feet) difference between GPS coordinates configured in GDA (based on global standard WGS 84) and AGD (used for most local maps), which is an unacceptably large error for some applications, such as surveying or site location for scuba diving.

Vertical datum

Further information: Chart datum

A vertical datum is a reference surface for vertical positions, such as the elevations of Earth features including terrain, bathymetry, water level, and man-made structures.

Geodetic coordinates

Further information: Earth:Geographic coordinate system

The same position on a spheroid has a different angle for latitude depending on whether the angle is measured from the normal line segment CP of the ellipsoid (angle α) or the line segment AP from the center (angle β). Note that the "flatness" of the spheroid (orange) in the image is greater than that of the Earth; as a result, the corresponding difference between the "geodetic" and "geocentric" latitudes is also exaggerated.

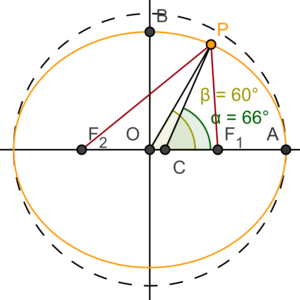
In geodetic coordinates, the Earth's surface is approximated by an ellipsoid, and locations near the surface are described in terms of latitude ([math]\displaystyle{ \phi }[/math]), longitude ([math]\displaystyle{ \lambda }[/math]), and height ([math]\displaystyle{ h }[/math]).

Geodetic versus geocentric latitude

Geodetic latitude and geocentric latitude represent similar quantities with different definitions. Geodetic latitude is defined as the angle between the equatorial plane and the surface normal at a point on the ellipsoid, whereas geocentric latitude is defined as the angle between the equatorial plane and a radial line connecting the centre of the ellipsoid to a point on the surface (see figure). When used without qualification, the term latitude refers to geodetic latitude. For example, the latitude used in geographic coordinates is geodetic latitude. The standard notation for geodetic latitude is φ. There is no standard notation for geocentric latitude; examples include θ, ψ, φ′.

Similarly, geodetic altitude is defined as the height above the ellipsoid surface, normal to the ellipsoid; whereas geocentric altitude is defined as the height above the ellipsoid surface along a line to the center of the ellipsoid (the radius). When used without qualification, the term altitude refers to geodetic altitude; as is used in aviation. Geocentric altitude is typically used in orbital mechanics.

Earth reference ellipsoid

Defining and derived parameters

The ellipsoid is completely parameterised by the semi-major axis [math]\displaystyle{ a }[/math] and the flattening [math]\displaystyle{ f }[/math].

Parameter	Symbol
Semi-major axis	[math]\displaystyle{ a }[/math]
Reciprocal of flattening	[math]\displaystyle{ \frac{1}{f} }[/math]

From [math]\displaystyle{ a }[/math] and [math]\displaystyle{ f }[/math] it is possible to derive the semi-minor axis [math]\displaystyle{ b }[/math], first eccentricity [math]\displaystyle{ e }[/math] and second eccentricity [math]\displaystyle{ e' }[/math] of the ellipsoid

Parameter	Value
Semi-minor axis	[math]\displaystyle{ b = a(1 - f) }[/math]
First eccentricity squared	[math]\displaystyle{ e^2 = 1 - \frac{b^2}{a^2} = f(2 - f) }[/math]
Second eccentricity squared	[math]\displaystyle{ {e'}^2 = \frac{a^2}{b^2} - 1 = \frac{f(2 - f)}{(1 - f)^2} }[/math]

Parameters for some geodetic systems

The two main reference ellipsoids used worldwide are the GRS80 and the WGS84.

A more comprehensive list of geodetic systems can be found here.

Geodetic Reference System 1980 (GRS80)

GRS80 parameters

Parameter	Notation	Value
Semi-major axis	[math]\displaystyle{ a }[/math]	6378137 m
Reciprocal of flattening	[math]\displaystyle{ \frac{1}{f} }[/math]	298.257222101

World Geodetic System 1984 (WGS 84)

The Global Positioning System (GPS) uses the World Geodetic System 1984 (WGS 84) to determine the location of a point near the surface of the Earth.

WGS 84 defining parameters

Parameter	Notation	Value
Semi-major axis	[math]\displaystyle{ a }[/math]	6378137.0 m
Reciprocal of flattening	[math]\displaystyle{ \frac{1}{f} }[/math]	298.257223563

WGS 84 derived geometric constants

Constant	Notation	Value
Semi-minor axis	[math]\displaystyle{ b }[/math]	6356752.3142 m
First eccentricity squared	[math]\displaystyle{ e^2 }[/math]	6.69437999014×10−3
Second eccentricity squared	[math]\displaystyle{ {e'}^2 }[/math]	6.73949674228×10−3

Conversion calculations

Further information: Earth:Geographic coordinate conversion

Datum conversion is the process of converting the coordinates of a point from one datum system to another. Datum conversion may frequently be accompanied by a change of grid projection.

Discussion and examples

A geodetic reference datum is a known and constant surface which is used to describe the location of unknown points on the Earth. Since reference datums can have different radii and different center points, a specific point on the Earth can have substantially different coordinates depending on the datum used to make the measurement. There are hundreds of locally developed reference datums around the world, usually referenced to some convenient local reference point. Contemporary datums, based on increasingly accurate measurements of the shape of the Earth, are intended to cover larger areas. The most common reference Datums in use in North America are NAD27, NAD83, and WGS 84.

The North American Datum of 1927 (NAD 27) is "the horizontal control datum for the United States that was defined by a location and azimuth on the Clarke spheroid of 1866, with origin at (the survey station) Meades Ranch (Kansas)." ... The geoidal height at Meades Ranch was assumed to be zero, as sufficient gravity data was not available, and this was needed to relate surface measurements to the datum. "Geodetic positions on the North American Datum of 1927 were derived from the (coordinates of and an azimuth at Meades Ranch) through a readjustment of the triangulation of the entire network in which Laplace azimuths were introduced, and the Bowie method was used." (http://www.ngs.noaa.gov/faq.shtml#WhatDatum ) NAD27 is a local referencing system covering North America.

The North American Datum of 1983 (NAD 83) is "The horizontal control datum for the United States, Canada, Mexico, and Central America, based on a geocentric origin and the Geodetic Reference System 1980 (GRS80). "This datum, designated as NAD 83 ...is based on the adjustment of 250,000 points including 600 satellite Doppler stations which constrain the system to a geocentric origin." NAD83 may be considered a local referencing system.

WGS 84 is the World Geodetic System of 1984. It is the reference frame used by the U.S. Department of Defense (DoD) and is defined by the National Geospatial-Intelligence Agency (NGA) (formerly the Defense Mapping Agency, then the National Imagery and Mapping Agency). WGS 84 is used by DoD for all its mapping, charting, surveying, and navigation needs, including its GPS "broadcast" and "precise" orbits. WGS 84 was defined in January 1987 using Doppler satellite surveying techniques. It was used as the reference frame for broadcast GPS Ephemerides (orbits) beginning January 23, 1987. At 0000 GMT January 2, 1994, WGS 84 was upgraded in accuracy using GPS measurements. The formal name then became WGS 84 (G730), since the upgrade date coincided with the start of GPS Week 730. It became the reference frame for broadcast orbits on June 28, 1994. At 0000 GMT September 30, 1996 (the start of GPS Week 873), WGS 84 was redefined again and was more closely aligned with International Earth Rotation Service (IERS) frame ITRF 94. It was then formally called WGS 84 (G873). WGS 84 (G873) was adopted as the reference frame for broadcast orbits on January 29, 1997. Another update brought it to WGS84(G1674).

The WGS 84 datum, within two meters of the NAD83 datum used in North America, is the only world referencing system in place today. WGS 84 is the default standard datum for coordinates stored in recreational and commercial GPS units.

Users of GPS are cautioned that they must always check the datum of the maps they are using. To correctly enter, display, and to store map related map coordinates, the datum of the map must be entered into the GPS map datum field.

Examples

Examples of map datums are:

• WGS 84, 72, 66 and 60 of the World Geodetic System
• NAD83, the North American Datum which is very similar to WGS 84
• NAD27, the older North American Datum, of which NAD83 was basically a readjustment [1]
• OSGB36 of the Ordnance Survey of Great Britain
• ETRS89, the European Datum, related to ITRS
• ED50, the older European Datum
• GDA94, the Australian Datum
• JGD2011, the Japanese Datum, adjusted for changes caused by 2011 Tōhoku earthquake and tsunami
• Tokyo97, the older Japanese Datum
• KGD2002, the Korean Datum
• TWD67 and TWD97, different datum currently used in Taiwan.
• BJS54 and XAS80, old geodetic datum used in China
• GCJ-02 and BD-09, Chinese encrypted geodetic datum.
• PZ-90.11, the current geodetic reference used by GLONASS
• GTRF, the geodetic reference used by Galileo
• CGCS2000, or CGS-2000, the geodetic reference used by BeiDou Navigation Satellite System
• International Terrestrial Reference Frames (ITRF88, 89, 90, 91, 92, 93, 94, 96, 97, 2000, 2005, 2008, 2014), different realizations of the ITRS.
• Hong Kong Principal Datum, a vertical datum used in Hong Kong.

See also

• Axes conventions
• ECEF
• ECI (coordinates)
• Engineering datum
• Figure of the Earth
• Geographic coordinate conversion
• Grid reference
• International Terrestrial Reference System
• Ordnance Datum
• World Geodetic System

Further reading

1. List of geodetic parameters for many systems from University of Colorado
2. Gaposchkin, E. M. and Kołaczek, Barbara (1981) Reference Coordinate Systems for Earth Dynamics Taylor & Francis ISBN:9789027712608
3. Kaplan, Understanding GPS: principles and applications, 1 ed. Norwood, MA 02062, USA: Artech House, Inc, 1996.
4. GPS Notes
5. P. Misra and P. Enge, Global Positioning System Signals, Measurements, and Performance. Lincoln, Massachusetts: Ganga-Jamuna Press, 2001.
6. Peter H. Dana: Geodetic Datum Overview – Large amount of technical information and discussion.
7. US National Geodetic Survey

External links

• GeographicLib includes a utility CartConvert which converts between geodetic and geocentric (ECEF) or local Cartesian (ENU) coordinates. This provides accurate results for all inputs including points close to the center of the Earth.
• A collection of geodetic functions that solve a variety of problems in geodesy in Matlab.
• NGS FAQ – What is a geodetic datum?
• About the surface of the Earth on kartoweb.itc.nl

es:Sistema de referencia geodésico zh:大地测量系统