Astronomy:Earth radius

Earth radius
13th century illustration of Earth in De sphaera mundi.
General information
Unit system	astronomy, geophysics
Unit of	distance
Symbol	R⊕ or [math]\displaystyle{ R_E }[/math], [math]\displaystyle{ \mathcal{R}^\mathrm N_\mathrm{eE} }[/math]
Conversions
1 R⊕ in ...	... is equal to ...
SI base unit	6.3781×106 m
Metric system	6,357 to 6,378 km
English units	3,950 to 3,963 mi

Earth radius is the distance from the center of Earth to a point on its surface. Its value ranges from 6,378 km (3,963 mi) at the equator to 6,357 km (3,950 mi) at a pole. A nominal Earth radius is sometimes used as a unit of measurement in astronomy and geophysics, denoted in astronomy by the symbol R_⊕. In other contexts, it is denoted [math]\displaystyle{ R_E }[/math] or sometimes [math]\displaystyle{ \mathcal{R}^\mathrm N_\mathrm{eE} }[/math].

The Earth is not a perfect sphere but approximately an oblate spheroid (an ellipse rotated around its minor axis) with a larger radius at the equator than at the poles. When only one radius is stated, the International Astronomical Union (IAU) prefers that it be the equatorial radius. The International Union of Geodesy and Geophysics (IUGG) recommends three values: the arithmetic mean of the radii measured at the equator and the poles (R₁); the authalic radius, which is the radius of a sphere with the same surface area (R₂); and the volumetric radius, which is the radius of a sphere having the same volume as the ellipsoid (R₃). All three values are about 6,371 kilometres (3,959 mi).

There are many other ways to define and measure the Earth radius. Some appear below. A few definitions yield values outside the range between polar radius and equatorial radius because they include local or geoidal topology or because they depend on abstract geometrical considerations.

Introduction

A scale diagram of the oblateness of the 2003 IERS reference ellipsoid, with north at the top. The light blue region is a circle. The outer edge of the dark blue line is an ellipse with the same minor axis as the circle and the same eccentricity as the Earth. The red line represents the Karman line 100 km (62 mi) above sea level, while the yellow area denotes the altitude range of the ISS in low Earth orbit.

Earth's rotation, internal density variations, and external tidal forces cause its shape to deviate systematically from a perfect sphere. Local topography increases the variance, resulting in a surface of profound complexity. Our descriptions of Earth's surface must be simpler than reality in order to be tractable. Hence, we create models to approximate characteristics of Earth's surface, generally relying on the simplest model that suits the need.

Each of the models in common use involve some notion of the geometric radius. Strictly speaking, spheres are the only solids to have radii, but broader uses of the term radius are common in many fields, including those dealing with models of Earth. The following is a partial list of models of Earth's surface, ordered from exact to more approximate:

• The actual surface of Earth
• The geoid, defined by mean sea level at each point on the real surface
• A spheroid, also called an ellipsoid of revolution, geocentric to model the entire Earth, or else geodetic for regional work
• A sphere

In the case of the geoid and ellipsoids, the fixed distance from any point on the model to the specified center is called "a radius of the Earth" or "the radius of the Earth at that point". It is also common to refer to any mean radius of a spherical model as "the radius of the earth". When considering the Earth's real surface, on the other hand, it is uncommon to refer to a "radius", since there is generally no practical need. Rather, elevation above or below sea level is useful.

Regardless of the model, any radius falls between the polar minimum of about 6,357 km and the equatorial maximum of about 6,378 km (3,950 to 3,963 mi). Hence, the Earth deviates from a perfect sphere by only a third of a percent, which supports the spherical model in most contexts and justifies the term "radius of the Earth". While specific values differ, the concepts in this article generalize to any major planet.

Physics of Earth's deformation

Rotation of a planet causes it to approximate an oblate ellipsoid/spheroid with a bulge at the equator and flattening at the North and South Poles, so that the equatorial radius a is larger than the polar radius b by approximately aq. The oblateness constant q is given by

[math]\displaystyle{ q=\frac{a^3 \omega^2}{GM}\,, }[/math]

where ω is the angular frequency, G is the gravitational constant, and M is the mass of the planet. For the Earth 1/q ≈ 289, which is close to the measured inverse flattening 1/f ≈ 298.257. Additionally, the bulge at the equator shows slow variations. The bulge had been decreasing, but since 1998 the bulge has increased, possibly due to redistribution of ocean mass via currents.

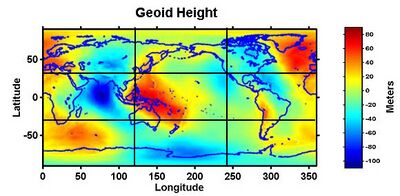
The variation in density and crustal thickness causes gravity to vary across the surface and in time, so that the mean sea level differs from the ellipsoid. This difference is the geoid height, positive above or outside the ellipsoid, negative below or inside. The geoid height variation is under 110 m (360 ft) on Earth. The geoid height can change abruptly due to earthquakes (such as the Sumatra-Andaman earthquake) or reduction in ice masses (such as Greenland).

Not all deformations originate within the Earth. Gravitational attraction from the Moon or Sun can cause the Earth's surface at a given point to vary by tenths of a meter over a nearly 12-hour period (see Earth tide).

Radius and local conditions

Al-Biruni's (973–1048) method for calculation of the Earth's radius simplified measuring the circumference compared to taking measurements from two locations distant from each other.

Given local and transient influences on surface height, the values defined below are based on a "general purpose" model, refined as globally precisely as possible within 5 m (16 ft) of reference ellipsoid height, and to within 100 m (330 ft) of mean sea level (neglecting geoid height).

Additionally, the radius can be estimated from the curvature of the Earth at a point. Like a torus, the curvature at a point will be greatest (tightest) in one direction (north–south on Earth) and smallest (flattest) perpendicularly (east–west). The corresponding radius of curvature depends on the location and direction of measurement from that point. A consequence is that a distance to the true horizon at the equator is slightly shorter in the north/south direction than in the east-west direction.

In summary, local variations in terrain prevent defining a single "precise" radius. One can only adopt an idealized model. Since the estimate by Eratosthenes, many models have been created. Historically, these models were based on regional topography, giving the best reference ellipsoid for the area under survey. As satellite remote sensing and especially the Global Positioning System gained importance, true global models were developed which, while not as accurate for regional work, best approximate the Earth as a whole.

Fixed radius

The following radii are derived from the World Geodetic System 1984 (WGS-84) standard ellipsoid. The standard ellipsoid is an idealized surface, and the Earth measurements used to calculate it have an uncertainty of ±2 m. in both the equatorial and polar dimensions. Additional discrepancies caused by orographic variation at specific locations can be significant. When identifying the position of an observable location, the use of more precise values for WGS-84 radii may not yield a corresponding improvement in accuracy.

The value for the equatorial radius is defined to the nearest 0.1 m in WGS-84. The value for the polar radius in this section has been rounded to the nearest 0.1 m, which is expected to be adequate for most uses. Refer to the WGS-84 ellipsoid if a more precise value for its polar radius is needed.

The symbol given for the named radius is used in the formulae found in this article.

Equatorial radius

The Earth's equatorial radius a, or semi-major axis, is the distance from its center to the equator and equals 6,378.1370 km (3,963.1906 mi). The equatorial radius is often used to compare Earth with other planets.

Polar radius

The Earth's polar radius b, or semi-minor axis, is the distance from its center to the North and South Poles, and equals 6,356.7523 km (3,949.9028 mi).

Location-dependent radii

Geocentric radius

The distance from the Earth's center to a point on the spheroid surface at geodetic latitude φ is:

[math]\displaystyle{ R(\varphi)=\sqrt{\frac{(a^2\cos\varphi)^2+(b^2\sin\varphi)^2}{(a\cos\varphi)^2+(b\sin\varphi)^2}} }[/math]

where a and b are, respectively, the equatorial radius and the polar radius.

Geophysical extremes

• Maximum: The summit of Chimborazo is 6,384.4 km (3,967.1 mi) from the Earth's center.
• Minimum: The floor of the Arctic Ocean is approximately 6,352.8 km (3,947.4 mi) from the Earth's center.

Radii of curvature

Principal sections

There are two principal radii of curvature: along the meridional and prime-vertical normal sections. The curvatures are the roots of Equation (125) in :

[math]\displaystyle{ (E G - F^2)\, \kappa^2 - ( e G + g E - 2 f F )\, \kappa + ( e g - f^2 ) = 0 =\det(A - \kappa\,B), }[/math]

where in the first fundamental form for a surface (Equation (112) in ):

[math]\displaystyle{ ds^2 = \sum_{ij} a_{ij} dw^i dw^j = E\, d\varphi^2 + 2 F\, d\varphi\, d\lambda + G\, d\lambda^2, }[/math]

E, F, and G are elements of the metric tensor:

[math]\displaystyle{ A = a_{ij} = \sum_{\nu} \frac{\partial r^{\nu}}{\partial w^i} \frac{\partial r^{\nu}}{\partial w^j} = \left[ \begin{array}{ll} E & F \\ F & G \end{array} \right], }[/math]

[math]\displaystyle{ r = [r^1, r^2, r^3]^T = [ x, y, z]^T }[/math], [math]\displaystyle{ w^1 = \varphi }[/math], [math]\displaystyle{ w^2 = \lambda, }[/math]

in the second fundamental form for a surface (Equation (123) in ):

[math]\displaystyle{ 2 D = \sum_{ij} b_{ij} dw^i dw^j = e\, d\varphi^2 + 2 f\, d \varphi\, d \lambda + g\, d \lambda^2, }[/math]

e, f, and g are elements of the shape tensor:

[math]\displaystyle{ B = b_{ij} = \sum_{\nu} n^{\nu} \frac{\partial ^2 r^{\nu}}{\partial w^i \partial w^j} = \left[ \begin{array}{ll} e & f \\ f & g \end{array} \right], }[/math]

[math]\displaystyle{ n = \frac{N}{|N|} }[/math] is the unit normal to the surface at [math]\displaystyle{ r }[/math], and because [math]\displaystyle{ \frac{\partial r}{\partial \varphi} }[/math] and [math]\displaystyle{ \frac{\partial r}{\partial \lambda} }[/math] are tangents to the surface,

[math]\displaystyle{ N = \frac{\partial r}{\partial \varphi} \times \frac{\partial r}{\partial \lambda} }[/math]

is normal to the surface at [math]\displaystyle{ r }[/math].

With [math]\displaystyle{ F = f = 0 }[/math] for an oblate spheroid, the curvatures are

[math]\displaystyle{ \kappa_1 = \frac{g}{G} }[/math] and [math]\displaystyle{ \kappa_2 = \frac{e}{E}\,, }[/math]

and the radii of curvature are

[math]\displaystyle{ R_1 = \frac{1}{\kappa_1} }[/math] and [math]\displaystyle{ R_2 = \frac{1}{\kappa_2}. }[/math]

Geometrically, the second fundamental form gives the distance from [math]\displaystyle{ r + dr }[/math] to the plane tangent at [math]\displaystyle{ r }[/math].

Meridional

In particular, the Earth's radius of curvature in the (north–south) meridian at φ is:

[math]\displaystyle{ M(\varphi)=R_1=\frac{(ab)^2}{\big((a\cos\varphi)^2+(b\sin\varphi)^2\big)^\frac32} =\frac{a(1-e^2)}{(1-e^2\sin^2\varphi)^\frac32} =\frac{1-e^2}{a^2} N(\varphi)^3\,. }[/math]

where [math]\displaystyle{ e }[/math] is the eccentricity of the earth. This is the radius that Eratosthenes measured.

Prime vertical

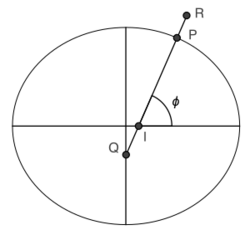
If one point had appeared due east of the other, one finds the approximate curvature in the east–west direction.

This radius of curvature in the prime vertical which is perpendicular (normal or orthogonal) to M at geodetic latitude φ is:

[math]\displaystyle{ N(\varphi)=R_2=\frac{a^2}{\sqrt{(a\cos\varphi)^2+(b\sin\varphi)^2}} =\frac{a}{\sqrt{1-e^2\sin^2\varphi}}\,. }[/math]

This radius is also called the transverse radius of curvature. At the equator, N = R. B. R. Bowring gives a geometric proof that this is the perpendicular distance from the surface to the polar axis.

Three different radii as a function of Earth's latitude. R is the geocentric radius; M is the meridional radius of curvature; and N is the prime vertical radius of curvature.

Particular values

The Earth's meridional radius of curvature at the equator equals the meridian's semi-latus rectum:

b²/a = 6,335.439 km

The Earth's polar radius of curvature is:

a²/b = 6,399.594 km

Directional

The Earth's radius of curvature along a course at an azimuth (measured clockwise from north) α at φ is derived from Euler's curvature formula as follows:

[math]\displaystyle{ R_\mathrm{c}=\frac{1}{\dfrac{\cos^2\alpha}{M}+\dfrac{\sin^2\alpha}{N}}\,. }[/math]

Combinations

It is possible to combine the principal radii of curvature above in a non-directional manner.

The Gaussian curvature is [math]\displaystyle{ K = \kappa_1\,\kappa_2 = \frac{\det\, B}{\det\, A} }[/math]. The Earth's Gaussian radius of curvature at latitude φ is:

[math]\displaystyle{ R_\mathrm{a}(\varphi)= \frac{1}{\sqrt{K}} = \frac{1}{2\pi}\int_{0}^{2\pi}R_\mathrm{c}(\alpha)\,d\alpha\,=\sqrt{MN}=\frac{a^2b}{(a\cos\varphi)^2+(b\sin\varphi)^2} =\frac{a\sqrt{1-e^2}}{1-e^2\sin^2\varphi}\,. }[/math]

The Earth's mean radius of curvature at latitude φ is:

[math]\displaystyle{ R_\mathrm{m}=\frac{2}{\dfrac{1}{M}+\dfrac{1}{N}}\,\! }[/math]

Global average radii

The Earth can be modeled as a sphere in many ways. This section describes the common ways. The various radii derived here use the notation and dimensions noted above for the Earth as derived from the WGS-84 ellipsoid; namely,

a = Equatorial radius (6378.1370 km)

b = Polar radius (6356.7523 km)

A sphere being a gross approximation of the spheroid, which itself is an approximation of the geoid, units are given here in kilometers rather than the millimeter resolution appropriate for geodesy.

Mean radius

Equatorial (a), polar (b) and mean Earth radii as defined in the 1984 World Geodetic System revision (not to scale)

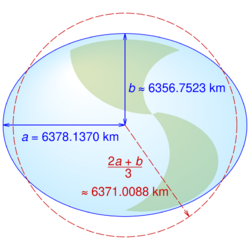
In geophysics, the International Union of Geodesy and Geophysics (IUGG) defines the mean radius (denoted R₁) to be

[math]\displaystyle{ R_1 = \frac{2a+b}{3}\,\! }[/math]

For Earth, the mean radius is 6,371.0088 km (3,958.7613 mi).

In astronomy, the International Astronomical Union denotes the nominal equatorial Earth radius as [math]\displaystyle{ \mathcal{R}^\mathrm N_\mathrm{eE} }[/math], which is defined to be 6,378.1 km (3,963.2 mi). The nominal polar Earth radius is defined as [math]\displaystyle{ \mathcal{R}^\mathrm N_\mathrm{pE} }[/math] = 6,356.8 km (3,949.9 mi). These values correspond to the zero tide radii. Equatorial radius is conventionally used as the nominal value unless the polar radius is explicitly required.

Authalic radius

Earth's authalic ("equal area") radius is the radius of a hypothetical perfect sphere that has the same surface area as the reference ellipsoid. The IUGG denotes the authalic radius as R₂.

A closed-form solution exists for a spheroid:

[math]\displaystyle{ R_2 =\sqrt{\frac{a^2+\frac{b^2}{e}\ln{\left(\frac{1+e}{b/a}\right)}}{2}} =\sqrt{\frac{a^2}2+\frac{b^2}2\frac{\tanh^{-1}e}e} =\sqrt{\frac{A}{4\pi}}\,, }[/math]

where e² = a² − b²/a² and A is the surface area of the spheroid.

For the Earth, the authalic radius is 6,371.0072 km (3,958.7603 mi).

Volumetric radius

Another spherical model is defined by the volumetric radius, which is the radius of a sphere of volume equal to the ellipsoid. The IUGG denotes the volumetric radius as R₃.

[math]\displaystyle{ R_3=\sqrt[3]{a^2b}\,. }[/math]

For Earth, the volumetric radius equals 6,371.0008 km (3,958.7564 mi).

Rectifying radius

Another mean radius is the rectifying radius, giving a sphere with circumference equal to the perimeter of the ellipse described by any polar cross section of the ellipsoid. This requires an elliptic integral to find, given the polar and equatorial radii:

[math]\displaystyle{ M_\mathrm{r}=\frac{2}{\pi}\int_{0}^{\frac{\pi}{2}}\sqrt{{a^2}\cos^2\varphi + {b^2} \sin^2\varphi}\,d\varphi\,. }[/math]

The rectifying radius is equivalent to the meridional mean, which is defined as the average value of M:

[math]\displaystyle{ M_\mathrm{r}=\frac{2}{\pi}\int_{0}^{\frac{\pi}{2}}\!M(\varphi)\,d\varphi\,. }[/math]

For integration limits of [0,π/2], the integrals for rectifying radius and mean radius evaluate to the same result, which, for Earth, amounts to 6,367.4491 km (3,956.5494 mi).

The meridional mean is well approximated by the semicubic mean of the two axes,

[math]\displaystyle{ M_\mathrm{r}\approx\left(\frac{a^\frac32+b^\frac32}{2}\right)^\frac23\,, }[/math]

which differs from the exact result by less than 1 μm (4×10⁻⁵ in); the mean of the two axes,

[math]\displaystyle{ M_\mathrm{r}\approx\frac{a+b}{2}\,, }[/math]

about 6,367.445 km (3,956.547 mi), can also be used.

Mean curvature

The mean curvature in all directions at all points on the surface is given by the weighted mean Gaussian curvature:

[math]\displaystyle{ R_4=\frac{1}{2}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\!\cos\varphi\,R_\mathrm{a}(\varphi)\,d\varphi=\frac{a}{2}\,\sqrt{\frac{1}{e^2}-1}\,\ln{\frac{1+e}{1-e}}. }[/math]

For the WGS 84 ellipsoid, the mean curvature equals 6,370.994 km (3,958.752 mi).

Average distance from center to surface

Most global mean radii are based on the reference ellipsoid, which approximates the geoid. The geoid has no direct relationship with surface topography, however. An alternative calculation averages elevations everywhere, resulting in a mean radius 230 m larger than the IUGG mean radius, the authalic radius, or the volumetric radius. This average is 6,371.230 km (3,958.899 mi) with uncertainty of 10 m (33 ft).

Osculating sphere

The best local spherical approximation to the ellipsoid in the vicinity of a given point is the osculating sphere. Its radius equals the Gaussian radius of curvature as above, and its radial direction coincides with the ellipsoid normal direction. The center of the osculating sphere is offset from the center of the ellipsoid, but is at the center of curvature for the given point on the ellipsoid surface. This concept aids the interpretation of terrestrial and planetary radio occultation refraction measurements and in some navigation and surveillance applications.

Published values

This table summarizes the accepted values of the Earth's radius.

Agency	Description	Value (in meters)	Ref
IAU	nominal "zero tide" equatorial	6378100
IAU	nominal "zero tide" polar	6356800
IUGG	equatorial radius	6378137
IUGG	semiminor axis (b)	6356752.3141
IUGG	polar radius of curvature (c)	6399593.6259
IUGG	mean radius (R1)	6371008.7714
IUGG	radius of sphere of same surface (R2)	6371007.1810
IUGG	radius of sphere of same volume (R3)	6371000.7900
IERS	WGS-84 ellipsoid, semi-major axis (a)	6378137.0
IERS	WGS-84 ellipsoid, semi-minor axis (b)	6356752.3142
IERS	WGS-84 first eccentricity squared (e2)	0.00669437999014
IERS	WGS-84 ellipsoid, polar radius of curvature (c)	6399593.6258
IERS	WGS-84 ellipsoid, Mean radius of semi-axes (R1)	6371008.7714
IERS	WGS-84 ellipsoid, Radius of Sphere of Equal Area (R2)	6371007.1809
IERS	WGS-84 ellipsoid, Radius of Sphere of Equal Volume (R3)	6371000.7900
	GRS 80 semi-major axis (a)	6378137.0
	GRS 80 semi-minor axis (b)	≈6356752.314140
	Spherical Earth Approx. of Radius (RE)	6366707.0195
	meridional radius of curvature at the equator	6335439
	Maximum (the summit of Chimborazo)	6384400
	Minimum (the floor of the Arctic Ocean)	6352800
	Average distance from center to surface	6371230±10

History

The first published reference to the Earth's size appeared around 350 BC, when Aristotle reported in his book On the Heavens that mathematicians had guessed the circumference of the Earth to be 400,000 stadia. Scholars have interpreted Aristotle's figure to be anywhere from highly accurate to almost double the true value. The first known scientific measurement and calculation of the circumference of the Earth was performed by Eratosthenes in about 240 BC. Estimates of the accuracy of Eratosthenes's measurement range from 0.5% to 17%. For both Aristotle and Eratosthenes, uncertainty in the accuracy of their estimates is due to modern uncertainty over which stadion length they meant.

See also

• Earth's circumference
• Earth mass
• Effective Earth radius
• Geodesy
• Geographical distance
• History of geodesy
• Template:Earth radius

External links

• Merrifield, Michael R. (2010). "[math]\displaystyle{ R_\oplus }[/math] The Earth's Radius (and exoplanets)". Sixty Symbols. Brady Haran for the University of Nottingham. http://www.sixtysymbols.com/videos/earthradius.htm.