Hanner polytope

In geometry, a Hanner polytope is a convex polytope constructed recursively by Cartesian product and polar dual operations. Hanner polytopes are named after Olof Hanner, who introduced them in 1956.

Construction

The Hanner polytopes are constructed recursively by the following rules:

• A line segment is a one-dimensional Hanner polytope.
• The Cartesian product of every two Hanner polytopes is another Hanner polytope, whose dimension is the sum of the dimensions of the two given polytopes.
• The dual of a Hanner polytope is another Hanner polytope of the same dimension.

They are exactly the polytopes that can be constructed using only these rules: that is, every Hanner polytope can be formed from line segments by a sequence of product and dual operations.

Alternatively and equivalently to the polar dual operation, the Hanner polytopes may be constructed by Cartesian products and direct sums, the dual of the Cartesian products. This direct sum operation combines two polytopes by placing them in two linearly independent subspaces of a larger space and then constructing the convex hull of their union.

Examples

The three-dimensional cube and its dual, the octahedron, the two three-dimensional Hanner polytopes

Schlegel diagram of the octahedral prism

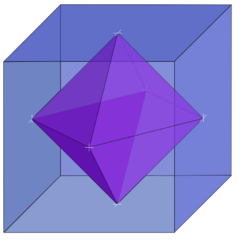
A cube is a Hanner polytope, and can be constructed as a Cartesian product of three line segments. Its dual, the octahedron, is also a Hanner polytope, the direct sum of three line segments. In three dimensions all Hanner polytopes are combinatorially equivalent to one of these two types of polytopes. In higher dimensions the hypercubes and cross polytopes, analogues of the cube and octahedron, are again Hanner polytopes. However, more examples are possible. For instance, the octahedral prism, a four-dimensional prism with an octahedron as its base is also a Hanner polytope, as is its dual, the cubical bipyramid.

Properties

Coordinate representation

Every Hanner polytope can be given vertex coordinates that are 0, 1, or −1. More explicitly, if P and Q are Hanner polytopes with coordinates in this form, then the coordinates of the vertices of the Cartesian product of P and Q are formed by concatenating the coordinates of a vertex in P with the coordinates of a vertex in Q. The coordinates of the vertices of the direct sum of P and Q are formed either by concatenating the coordinates of a vertex in P with a vector of zeros, or by concatenating a vector of zeros with the coordinates of a vertex in Q.

Because the polar dual of a Hanner polytope is another Hanner polytope, the Hanner polytopes have the property that both they and their duals have coordinates in {0,1,−1}.

Number of faces

Every Hanner polytope is centrally symmetric, and has exactly 3^d nonempty faces (including the polytope itself as a face but not including the empty set). For instance, the cube has 8 vertices, 12 edges, 6 squares, and 1 cube (itself) as faces; 8 + 12 + 6 + 1 = 27 = 3³. The Hanner polytopes form an important class of examples for Kalai's 3^d conjecture that all centrally symmetric polytopes have at least 3^d nonempty faces.

Pairs of opposite facets and vertices

In a Hanner polytope, every two opposite facets are disjoint, and together include all of the vertices of the polytope, so that the convex hull of the two facets is the whole polytope. As a simple consequence of this fact, all facets of a Hanner polytope have the same number of vertices as each other (half the number of vertices of the whole polytope). However, the facets may not all be isomorphic to each other. For instance, in the octahedral prism, two of the facets are octahedra, and the other eight facets are triangular prisms. Dually, in every Hanner polytope, every two opposite vertices touch disjoint sets of facets, and together touch all of the facets of the polytope.

Mahler volume

The Mahler volume of a Hanner polytope (the product of its volume and the volume of its polar dual) is the same as for a cube or cross polytope. If the Mahler conjecture is true, these polytopes are the minimizers of Mahler volume among all the centrally symmetric convex bodies.

Helly property

The translates of a hypercube (or of an affine transformation of it, a parallelotope) form a Helly family: every set of translates that have nonempty pairwise intersections has a nonempty intersection. Moreover, these are the only convex bodies with this property. For any other centrally symmetric convex polytope K, (Hanner 1956) defined I(K) to be the smallest number of translates of K that do not form a Helly family (they intersect pairwise but have an empty intersection). He showed that I(K) is either three or four, and gave the Hanner polytopes as examples of polytopes for which it is four. (Hansen Lima) later showed that this property can be used to characterize the Hanner polytopes: they are (up to affine transformation) exactly the polytopes for which I(K) > 3.

Combinatorial enumeration

The number of combinatorial types of Hanner polytopes of dimension d is the same as the number of simple series–parallel graphs with d unlabeled edges. For d = 1, 2, 3, ... it is:

1, 1, 2, 4, 8, 18, 40, 94, 224, 548, ... (sequence A058387 in the OEIS).

A more explicit bijection between the Hanner polytopes of dimension d and the cographs with d vertices is given by (Reisner 1991). For this bijection, the Hanner polytopes are assumed to be represented geometrically using coordinates in {0,1,−1} rather than as combinatorial equivalence classes; in particular, there are two different geometric forms of a Hanner polytope even in two dimensions, the square with vertex coordinates (±1,±1) and the diamond with vertex coordinates (0,±1) and (±1,0). Given a d-dimensional polytope with vertex coordinates in {0,1,−1}, Reisner defines an associated graph whose d vertices correspond to the unit vectors of the space containing the polytope, and for which two vectors are connected by an edge if their sum lies outside the polytope. He observes that the graphs of Hanner polytopes are cographs, which he characterizes in two ways: the graphs with no induced path of length three, and the graphs whose induced subgraphs are all either disconnected or the complements of disconnected graphs. Conversely, every cograph can be represented in this way by a Hanner polytope.

Hanner spaces

The Hanner polytopes are the unit balls of a family of finite-dimensional Banach spaces called Hanner spaces. The Hanner spaces are the spaces that can be built up from one-dimensional spaces by [math]\displaystyle{ \ell_1 }[/math] and [math]\displaystyle{ \ell_\infty }[/math] combinations.