Harmonic progression (mathematics)
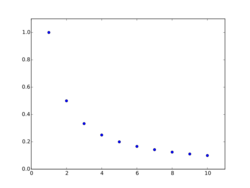
In mathematics, a harmonic progression (or harmonic sequence) is a progression formed by taking the reciprocals of an arithmetic progression.
Equivalently, a sequence is a harmonic progression when each term is the harmonic mean of the neighboring terms.
As a third equivalent characterization, it is an infinite sequence of the form
- [math]\displaystyle{ \frac{1}{a},\ \frac{1}{a+d},\ \frac{1}{a+2d},\ \frac{1}{a+3d}, \cdots, }[/math]
where a is not zero and −a/d is not a natural number, or a finite sequence of the form
- [math]\displaystyle{ \frac{1}{a},\ \frac{1}{a+d},\ \frac{1}{a+2d},\ \frac{1}{a+3d}, \cdots,\ \frac{1}{a+kd}, }[/math]
where a is not zero, k is a natural number and −a/d is not a natural number or is greater than k.
Examples
In the following n is a natural number, in sequence: [math]\displaystyle{ \ n = 1,\ 2,\ 3,\ 4,\ \ldots\ }[/math]
- [math]\displaystyle{ 1, \tfrac{\ 1\ }{2},\ \tfrac{\ 1\ }{3},\ \tfrac{\ 1\ }{4},\ \tfrac{\ 1\ }{5},\ \tfrac{\ 1\ }{6},\ \ldots \ , \ \tfrac{\ 1\ }{n},\ \ldots \ }[/math] is called the harmonic sequence
- 12, 6, 4, 3, [math]\displaystyle{ \ \tfrac{12}{\ 5\ },\ 2,\ \ldots\ ,\ \tfrac{12}{\ n\ },\ \ldots\ }[/math]
- 30, −30, −10, −6, [math]\displaystyle{ \ -\tfrac{30}{\ 7\ },\ \ldots\ ,\ \tfrac{30}{\ \left( 3\ -\ 2 n \right)\ },\ \ldots\ }[/math]
- 10, 30, −30, −10, −6, [math]\displaystyle{ \ \ldots\ \tfrac{30}{\ \left( 5\ -\ 2 n \right)\ },\ \ldots\ }[/math]
Sums of harmonic progressions
Infinite harmonic progressions are not summable (sum to infinity).
It is not possible for a harmonic progression of distinct unit fractions (other than the trivial case where a = 1 and k = 0) to sum to an integer. The reason is that, necessarily, at least one denominator of the progression will be divisible by a prime number that does not divide any other denominator.[1]
Use in geometry
If collinear points A, B, C, and D are such that D is the harmonic conjugate of C with respect to A and B, then the distances from any one of these points to the three remaining points form harmonic progression.[2][3] Specifically, each of the sequences AC, AB, AD; BC, BA, BD; CA, CD, CB; and DA, DC, DB are harmonic progressions, where each of the distances is signed according to a fixed orientation of the line.
In a triangle, if the altitudes are in arithmetic progression, then the sides are in harmonic progression.
Leaning Tower of Lire
An excellent example of Harmonic Progression is the Leaning Tower of Lire. In it, uniform blocks are stacked on top of each other to achieve the maximum sideways or lateral distance covered. The blocks are stacked 1/2, 1/4, 1/6, 1/8, 1/10, … distance sideways below the original block. This ensures that the center of gravity is just at the center of the structure so that it does not collapse. A slight increase in weight on the structure causes it to become unstable and fall.
See also
References
- ↑ Erdős, P. (1932), "Egy Kürschák-féle elemi számelméleti tétel általánosítása" (in Hungarian), Mat. Fiz. Lapok 39: 17–24, https://www.renyi.hu/~p_erdos/1932-02.pdf. As cited by "Paul Erdős and Egyptian fractions", Erdős centennial, Bolyai Soc. Math. Stud., 25, János Bolyai Math. Soc., Budapest, 2013, pp. 289–309, doi:10.1007/978-3-642-39286-3_9, ISBN 978-3-642-39285-6.
- ↑ Chapters on the modern geometry of the point, line, and circle, Vol. II by Richard Townsend (1865) p. 24
- ↑ Modern geometry of the point, straight line, and circle: an elementary treatise by John Alexander Third (1898) p. 44
- Mastering Technical Mathematics by Stan Gibilisco, Norman H. Crowhurst, (2007) p. 221
- Standard mathematical tables by Chemical Rubber Company (1974) p. 102
- Essentials of algebra for secondary schools by Webster Wells (1897) p. 307
| Integer sequences |
|  | ||||
|---|---|---|---|---|---|---|
| Properties of sequences | ||||||
| Properties of series | ||||||
| Explicit series | ||||||
| Kinds of series | ||||||
| Hypergeometric series | ||||||
 |  |
