Hesse configuration
| Hesse configuration | |
|---|---|
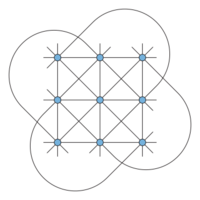 The Hesse configuration, with four of its lines (the four broken diagonals of the 3×3 array of points) drawn as curves | |
| Named after | Otto Hesse |
| Vertices | 9 |
| Edges | 12 |
| Diameter | 1 |
| Automorphisms | 432 |
| Notation | (94 123) |
| Table of graphs and parameters | |
In geometry, the Hesse configuration is a configuration of 9 points and 12 lines with three points per line and four lines through each point. It can be denoted as (94 123) or configuration matrix . It is symmetric (point and line transitive) with 432 automorphisms.
It can be realized in the complex projective plane as the set of inflection points of an elliptic curve, but it has no realization in the Euclidean plane. It was introduced by Colin Maclaurin and studied by Hesse (1844),[1] and is also known as Young's geometry,[2] named after the later work of John Wesley Young on finite geometry.[3][4]
Description
The Hesse configuration has the same incidence relations as the lines and points of the affine plane over the field of 3 elements. That is, the points of the Hesse configuration may be identified with ordered pairs of numbers modulo 3, and the lines of the configuration may correspondingly be identified with the triples of points (x, y) satisfying a linear equation ax + by = c (mod 3). Alternatively, the points of the configuration may be identified by the squares of a tic-tac-toe board, and the lines may be identified with the lines and broken diagonals of the board.
Each point belongs to four lines: in the tic tac toe interpretation of the configuration, one line is horizontal, one vertical, and two are diagonals or broken diagonals. Each line contains three points. In the language of configurations the Hesse configuration has the notation (94 123), meaning that there are 9 points, 4 lines per point, 12 lines, and 3 points per line.
With points indexed 1...9 in a 3x3 grid, can have configuration table. Columns are lines, indexing points.
| Horizontal | Vertical | Diag-1 | Diag-2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 7 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 2 | 5 | 8 | 4 | 5 | 6 | 5 | 6 | 4 | 6 | 4 | 5 |
| 3 | 6 | 9 | 7 | 8 | 9 | 9 | 7 | 8 | 8 | 9 | 7 |
The Hesse configuration has 18×4! = 432 automorphisms, doubling the symmetries of the related Hessian group.
Every pair of points are connected within one line. This is seen in its complete adjacency matrix:
Related configurations

- Dual configuration
The dual configuration, (123 94), points indexed 1...12 can have configuration table:
| 1 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| 2 | 5 | 8 | 5 | 7 | 5 | 6 | 6 | 7 |
| 3 | 6 | 9 | 8 | 9 | 10 | 9 | 8 | 10 |
| 4 | 7 | 10 | 11 | 12 | 12 | 11 | 12 | 11 |
- Möbius–Kantor configuration
Removing any one point and its four incident lines from the Hesse configuration produces self dual configuration (83) or , the Möbius–Kantor configuration.[5][6][7] It has 48 automorphisms.
(83) is a cyclic configuration, defined by one generator line as {0,1,3}8, with following lines with incremented indices modulo 8.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 |
| 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 |
- Pappus configuration
In the Hesse configuration, the 12 lines may be grouped into four triples of parallel (non-intersecting) lines, (93 33+33+33+33). This is seen as the horizontal, vertical and 2 sets of diagonal lines.
Removing from the Hesse configuration the three lines belonging to a single triple produces a self dual configuration (93) or , the Pappus configuration.[6][7] The Pappus configuration has 18×3! = 108 automorphisms.
| Horizontal | Vertical | Diag-1 | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 4 | 7 | 1 | 2 | 3 | 1 | 2 | 3 |
| 2 | 5 | 8 | 4 | 5 | 6 | 5 | 6 | 4 |
| 3 | 6 | 9 | 7 | 8 | 9 | 9 | 7 | 8 |
- Dual of K3,3 graph

Removing half of the triples from the Hess configuration leaves (92 63) or , which is represented in the regular complex polygon 3{4}2, 9 vertices and 6 3-edges. It is also the dual configuration of complete bipartite graph, K3,3, called the utility graph (or Thomsen graph), (63 92) or , with 2×(3!)2 = 72 automorphisms.
| Horizontal | Vertical | ||||
|---|---|---|---|---|---|
| 1 | 4 | 7 | 1 | 2 | 3 |
| 2 | 5 | 8 | 4 | 5 | 6 |
| 3 | 6 | 9 | 7 | 8 | 9 |
PG(2,3)

The Hesse configuration may in turn be augmented by adding four points, one for each triple of non-intersecting lines, and one line containing the four new points, to form self dual configuration (134) or .
It is isomorphic to PG(2,3), the set of points and lines of the projective plane over the three-element field.[8][9]
PG(2,k) has (k3-1)(k3-k)(k3-k2)/(k-1) automorphisms with prime k, here (33-1)(33-3)(33-32)/(2-1)=26⋅24⋅18/2 = 5616 automorphisms, 13× higher than Hesse configuration.
| Diag-1 | Horizontal | Diag-2 | Vertical | New | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 4 | 7 | 1 | 2 | 3 | 1 | 2 | 3 | 10 |
| 6 | 4 | 5 | 2 | 5 | 8 | 5 | 6 | 4 | 4 | 5 | 6 | 11 |
| 8 | 9 | 7 | 3 | 6 | 9 | 9 | 7 | 8 | 7 | 8 | 9 | 12 |
| 10 | 10 | 10 | 11 | 11 | 11 | 12 | 12 | 12 | 13 | 13 | 13 | 13 |
(134) is also a cyclic configuration, with a generator "line" as {0,1,4,6}13. (Sequential lines increment vertex indices by 1 modulo 13.)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 0 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 0 | 1 | 2 | 3 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 | 0 | 1 | 2 | 3 | 4 | 5 |
Realizability
The Hesse configuration can be realized in the complex projective plane as the 9 inflection points of an elliptic curve and the 12 lines through triples of inflection points.[3] If a given set of nine points in the complex plane is the set of inflections of an elliptic curve C, it is also the set of inflections of every curve in a pencil of curves generated by C and by the Hessian curve of C, the Hesse pencil.[10]
The Hessian polyhedron is a representation of the Hesse configuration in the complex plane.
The Hesse configuration shares with the Möbius–Kantor configuration the property of having a complex realization but not being realizable by points and straight lines in the Euclidean plane. In the Hesse configuration, every two points are connected by a line of the configuration (the defining property of the Sylvester–Gallai configurations) and therefore every line through two of its points contains a third point. But in the Euclidean plane, every finite set of points is either collinear, or includes a pair of points whose line does not contain any other points of the set; this is the Sylvester–Gallai theorem. Because the Hesse configuration disobeys the Sylvester–Gallai theorem, it has no Euclidean realization. This example also shows that the Sylvester–Gallai theorem cannot be generalized to the complex projective plane. However, in complex spaces, the Hesse configuration and all Sylvester–Gallai configurations must lie within a two-dimensional flat subspace.[11]
References
- ↑ Hesse, O. (1844), "Über die Elimination der Variabeln aus drei algebraischen Gleichungen vom zweiten Grade mit zwei Variabeln" (in German), Journal für die Reine und Angewandte Mathematik 28: 68–96, doi:10.1515/crll.1844.28.68, ISSN 0075-4102, https://zenodo.org/record/1448844/files/article.pdf.
- ↑ Wallace, Edward C.; West, Stephen F. (2015), Roads to Geometry (3rd ed.), Waveland Press, pp. 23–24, ISBN 9781478632047, https://books.google.com/books?id=7kTsCgAAQBAJ&pg=PA23
- ↑ 3.0 3.1 MacNeish, H. F. (1942), "Four finite geometries", The American Mathematical Monthly 49: 15–23, doi:10.2307/2303772
- ↑ Projective Geometry, I, Ginn and Company, 1910, p. 249, https://archive.org/details/projectivegeomet004116mbp/page/n257
- ↑ "Abstract configurations in algebraic geometry", The Fano Conference, Univ. Torino, Turin, 2004, pp. 423–462.
- ↑ 6.0 6.1 Coxeter, H. S. M. (1950), "Self-dual configurations and regular graphs", Bulletin of the American Mathematical Society 56 (5): 413–455, doi:10.1090/S0002-9904-1950-09407-5.
- ↑ 7.0 7.1 Cullinane, Steven H. (2011), Configurations and squares, http://finitegeometry.org/sc/gen/configs.html.
- ↑ Batten, Lynn Margaret (1997), Combinatorics of finite geometries, Second edition, Cambridge University, p. 41-42
- ↑ On the Levi graph of point-line configurations, Jessica Hauschild, Jazmin Ortiz and Oscar Vega (2015)
- ↑ Artebani, Michela; Dolgachev, Igor (2009), "The Hesse pencil of plane cubic curves", L'Enseignement Mathématique, 2e Série 55 (3): 235–273, doi:10.4171/lem/55-3-3.
- ↑ "Sylvester–Gallai theorems for complex numbers and quaternions", Discrete and Computational Geometry 35 (3): 361–373, 2006, doi:10.1007/s00454-005-1226-7.
 |
