Hexagonal Efficient Coordinate System

From HandWiki

The Hexagonal Efficient Coordinate System (HECS), formerly known as Array Set Addressing (ASA), is a coordinate system for hexagonal grids that allows hexagonally sampled images to be efficiently stored and processed on digital systems. HECS represents the hexagonal grid as a set of two interleaved rectangular sub-arrays, which can be addressed by normal integer row and column coordinates and are distinguished with a single binary coordinate. Hexagonal sampling is the optimal approach for isotropically band-limited two-dimensional signals[1] and its use provides a sampling efficiency improvement of 13.4% over rectangular sampling. The HECS system enables the use of hexagonal sampling for digital imaging applications without requiring significant additional processing to address the hexagonal array.[2]

Introduction

The advantages of sampling on a hexagonal grid instead of the standard rectangular grid for digital imaging applications include: more efficient sampling, consistent connectivity, equidistant neighboring pixels, greater angular resolution, and higher circular symmetry.[3][4][5] Sometimes, more than one of these advantages compound together, thereby increasing the efficiency by 50% in terms of computation and storage when compared to rectangular sampling.[6] Researchers have shown[1][6][7] that the hexagonal grid is the optimal sampling lattice and its use provides a sampling efficiency improvement of 13.4% over rectangular sampling for isotropically band-limited two-dimensional signals. Despite all of these advantages of hexagonal sampling over rectangular sampling, its application has been limited because of the lack of an efficient coordinate system.[8] However that limitation has been removed with the recent[when?] development of HECS.

Hexagonal Efficient Coordinate System

Description

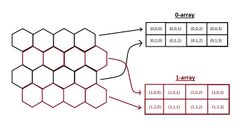
Representation of hexagonally sampled data as a pair of rectangular arrays using the HECS coordinate system

The Hexagonal Efficient Coordinate System (HECS) is based on the idea of representing the hexagonal grid as a set of two rectangular arrays which can be individually indexed using familiar integer-valued row and column indices. The arrays are distinguished using a single binary coordinate so that a full address for any point on the hexagonal grid is uniquely represented by three coordinates.[9]

[math]\displaystyle{ (a,r,c) \in \{ 0,1 \} \times \mathbb Z\times\mathbb Z }[/math]

where the coordinates represent the array, row, and column, respectively. The hexagonal grid is separated into rectangular arrays by taking every other row as one array and the remaining rows as the other array, as shown in the figure.

Nearest neighbors

Nearest neighbors of a HECS pixel

The addresses of the nearest neighbors of a pixel (or grid point) are easily determined by simple expressions which are functions of the pixel's coordinates, as shown.

Convert to Cartesian

Converting coordinates in HECS to their Cartesian counterparts is done with a simple matrix multiplication

[math]\displaystyle{ \begin{bmatrix} x\\y \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & 0 & 1 \\ \frac{\sqrt{3}}{2} & \sqrt{3} & 0 \end{bmatrix}\begin{bmatrix} a\\r\\c \end{bmatrix} = \begin{bmatrix} \frac{a}{2} + c \\(\sqrt{3})(\frac{a}{2} + r) \end{bmatrix}. }[/math]

Operators

Preliminaries

Let the set of all possible HECS addresses be [math]\displaystyle{ \text{HECS} = \{ 0,1 \} \times \mathbb Z \times\mathbb Z. }[/math]

[math]\displaystyle{ \mathbf{p}_i =\begin{bmatrix} a_i\\r_i\\c_i \end{bmatrix} \in \text{HECS}. }[/math]
[math]\displaystyle{ \mathbf{p} =\begin{bmatrix} a\\r\\c \end{bmatrix} \in \text{HECS}. }[/math]
[math]\displaystyle{ k \in \mathbb N. }[/math]

Addition

A binary addition operator [math]\displaystyle{ (\text{HECS},+) }[/math] has been defined as

[math]\displaystyle{ \mathbf{p}_1 + \mathbf{p}_2=\begin{bmatrix} a_1 \oplus a_2\\r_1 + r_2 + (a_1 \land a_2)\\c_1 + c_2 + (a_1 \land a_2) \end{bmatrix}, }[/math]

where [math]\displaystyle{ \oplus }[/math] is the logical XOR operator and [math]\displaystyle{ \land }[/math] is the logical AND operator.

Negation

A unary negation operator [math]\displaystyle{ (\text{HECS},-) }[/math] has been defined as

[math]\displaystyle{ -\mathbf{p} =\begin{bmatrix} a\\-r-a\\-c-a \end{bmatrix}. }[/math]

Subtraction

A binary subtraction operator [math]\displaystyle{ (\text{HECS},-) }[/math] has been defined by combining the negation and addition operations as

[math]\displaystyle{ \mathbf{p}_1-\mathbf{p}_2 = \mathbf{p}_1 + (-\mathbf{p}_2). }[/math]

Scalar multiplication

Scalar multiplication has been defined for non-negative integer scalar multipliers as

[math]\displaystyle{ k\mathbf{p}=\begin{bmatrix} (ak) \bmod 2\\kr + (a)\left\lfloor \frac{k}{2} \right\rfloor \\kc + (a)\left\lfloor \frac{k}{2} \right\rfloor \end{bmatrix}, }[/math]

and

[math]\displaystyle{ -k\mathbf{p}=k(-\mathbf{p}). }[/math]

Separable Fourier kernel

The hexagonal discrete Fourier transform (HDFT) was developed by Mersereau[6] and was converted to an HECS representation by Rummelt.[2] Let [math]\displaystyle{ x(a, r, c) }[/math] be a two-dimensional hexagonally sampled signal and let both arrays be of size [math]\displaystyle{ n\times m }[/math]. Let [math]\displaystyle{ X(b, s, d) }[/math] be the Fourier transform of x. The HDFT equation for the forward transform is given by

[math]\displaystyle{ X(b, s, d) = \sum_{a} \sum_r \sum_c x(a, r, c) \exp\left[-j\pi\left(\frac{(a+2c)(b+2d)}{2m} + \frac{(a+2r)(b+2s)}{n} \right) \right] }[/math]

Notice that the HECS representation of the HDFT overcomes Mersereau's "insurmountable difficulty" since it is a separable kernel, which led to the development of the hexagonal fast Fourier transform.[10]

Alternative addressing schemes

There have been several attempts to develop efficient coordinate systems for the hexagonal grid. Snyder[4] describes a coordinate system based on non-orthogonal bases which is referred to as the h2 system. Her[11] developed an interesting three-coordinate system that uses an oblique plane in three dimensional space. For various reasons, both of these approaches require cumbersome machine representations that lead to inefficient image processing operations.[8] Generalized balanced ternary (GBT) is based on a hierarchy of cells, where at every level the cells are each aggregates of cells from the previous level.[12] In two-dimensions, GBT can be used to address the hexagonal grid where each grid point is addressed with a string of base-7 digits and each digit indicates the hexagon's position within that level of the hierarchy.[13] The use of GBT and slightly modified versions of GBT such as HIP[14] and Spiral Architecture[15] for addressing hexagonal grids in two dimensions are abundant in the literature.[5][14][15][16] While these approaches have some interesting mathematical properties, they fail to be convenient or efficient for image processing.[8]

Other 2D hexagonal grid applications

Although HECS was developed mainly for digital image processing of hexagonally sampled images, its benefits extend to other applications such as finding the shortest path distance and shortest path routing between points in hexagonal interconnection networks.[8] Other addressing approaches have been developed for such applications[17][18][19] but they suffer the same drawbacks as the ones described above.[8]

References

  1. ↑ 1.0 1.1 Petersen, Daniel P.; Middleton, David (December 1962). "Sampling and reconstruction of wave-number-limited functions in N-dimensional euclidean spaces" (in en). Information and Control 5 (4): 279–323. doi:10.1016/S0019-9958(62)90633-2. https://linkinghub.elsevier.com/retrieve/pii/S0019995862906332. 
  2. ↑ 2.0 2.1 Rummelt, Nicholas I. (2010). Array Set Addressing: Enabling Efficient Hexagonally Sampled Image Processing (Ph.D. thesis). University of Florida.
  3. ↑ Xiangjian He; Wenjing Jia (27–28 August 2005). "Hexagonal Structure for Intelligent Vision". 2005 International Conference on Information and Communication Technologies. IEEE. pp. 52–64. doi:10.1109/ICICT.2005.1598543. ISBN 978-0-7803-9421-6. https://ieeexplore.ieee.org/document/1598543/. 
  4. ↑ 4.0 4.1 Snyder, Wesley E.; Qi, Hairong; Sander, William A. (1999-05-21). "Coordinate system for hexagonal pixels". in Hanson, Kenneth M.. Medical Imaging 1999: Image Processing. 3661. SPIE. pp. 716–727. doi:10.1117/12.348629. http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=980707. 
  5. ↑ 5.0 5.1 van Roessel, Jan W. (1988). "Conversion of Cartesian coordinates from and to Generalized Balanced Ternary addresses". Photogrammetric Engineering and Remote Sensing 54: 1565–1570. https://www.asprs.org/wp-content/uploads/pers/1988journal/nov/1988_nov_1565-1570.pdf. 
  6. ↑ 6.0 6.1 6.2 Mersereau, R.M. (June 1979). "The processing of hexagonally sampled two-dimensional signals". Proceedings of the IEEE 67 (6): 930–949. doi:10.1109/PROC.1979.11356. ISSN 0018-9219. http://ieeexplore.ieee.org/document/1455625/. 
  7. ↑ Vitulli, R.; Del Bello, U.; Armbruster, P.; Baronti, S.; Santurti, L. (24–28 June 2002). "Aliasing effects mitigation by optimised sampling grids and impact on image acquisition chains". IEEE International Symposium on Geoscience and Remote Sensing (IGARSS). 2. IEEE. pp. 979–981. doi:10.1109/IGARSS.2002.1025749. ISBN 978-0-7803-7536-9. http://ieeexplore.ieee.org/document/1025749/. 
  8. ↑ 8.0 8.1 8.2 8.3 8.4 Rummelt, Nicholas I.; Wilson, Joseph N. (2011-04-01). "Array set addressing: enabling technology for the efficient processing of hexagonally sampled imagery" (in en). Journal of Electronic Imaging 20 (2): 023012. doi:10.1117/1.3589306. ISSN 1017-9909. http://electronicimaging.spiedigitallibrary.org/article.aspx?doi=10.1117/1.3589306. 
  9. ↑ Rummelt, Nicholas I., "Array set addressing (ASA) for hexagonally arranged data sampling elements", US patent 8797436, issued August 5, 2014 This article incorporates text from this source, which is in the public domain.
  10. ↑ Birdsong, James B.; Rummelt, Nicholas I. (25–28 September 2016). "The hexagonal fast fourier transform". IEEE International Conference on Image Processing (ICIP). IEEE. pp. 1809–1812. doi:10.1109/ICIP.2016.7532670. ISBN 978-1-4673-9961-6. http://ieeexplore.ieee.org/document/7532670/. 
  11. ↑ I. Her, “A symmetrical coordinate frame on the hexagonal grid for computer graphics and vision,” J. Mech. Des. 115, 447–449 (1993)
  12. ↑ D. Lucas and L. Gibson, “A system for hierarchical addressing in Euclidean space,” Interactive Systems Corporation (1980).
  13. ↑ L. Gibson and C. Lenzmeier, “A hierarchical pattern extraction system for hexagonally sampled images,” Tech. Rep., Final Report for Contract F49620-81-C-0039, U.S. Air Force Office of Scientific Research, Interactive Systems Corporation (1981)
  14. ↑ 14.0 14.1 L. Middleton and J. Sivaswamy, Hexagonal Image Processing: A Practical Approach (Springer, London, 2005)
  15. ↑ 15.0 15.1 P. Sheridan, “Spiral architecture for machine vision,” Ph.D. thesis, Univ. of Technology Sydney (1996)
  16. ↑ A. Vince and X. Zheng, “Computing the discrete Fourier transform on a hexagonal lattice,” J. Math. Imaging Vision 28, 125–133 (2007)
  17. ↑ Carle, J.; Myoupo, J.F. (14–17 May 2000). "Topological properties and optimal routing algorithms for three dimensional hexagonal networks". Fourth International Conference on High Performance Computing in the Asia-Pacific Region. 1. IEEE. pp. 116–121 vol.1. doi:10.1109/HPC.2000.846530. https://ieeexplore.ieee.org/document/846530/. 
  18. ↑ Garcia Nocetti, F.; Stojmenovic, I.; Jingyuan Zhang (September 2002). "Addressing and routing in hexagonal networks with applications for tracking mobile users and connection rerouting in cellular networks" (in en). IEEE Transactions on Parallel and Distributed Systems 13 (9): 963–971. doi:10.1109/TPDS.2002.1036069. ISSN 1045-9219. http://ieeexplore.ieee.org/document/1036069/. 
  19. ↑ M. He and W. Xiao, “A unified addressing schema for hexagonal and honeycomb networks with isomorphic cayley graphs,” in Proc. 1st Int. Multi-Symp. on Computer and Computational Sciences (IMSCCS ’06), Vol. 1, pp. 363–368 (2006).



Retrieved from "https://handwiki.org/wiki/index.php?title=Hexagonal_Efficient_Coordinate_System&oldid=3358918"