Homogeneous relation

From HandWiki
Short description: Binary relation over a set and itself

In mathematics, a homogeneous relation (also called endorelation) on a set X is a binary relation between X and itself, i.e. it is a subset of the Cartesian product X × X.[1][2][3] This is commonly phrased as "a relation on X"[4] or "a (binary) relation over X".[5][6] An example of a homogeneous relation is the relation of kinship, where the relation is between people.

Common types of endorelations include orders, graphs, and equivalences. Specialized studies of order theory and graph theory have developed understanding of endorelations. Terminology particular for graph theory is used for description, with an ordinary graph presumed to correspond to a symmetric relation, and a general endorelation corresponding to a directed graph. An endorelation R corresponds to a logical matrix of 0s and 1s, where the expression xRy corresponds to an edge between x and y in the graph, and to a 1 in the square matrix of R. It is called an adjacency matrix in graph terminology.

Particular homogeneous relations

Some particular homogeneous relations over a set X (with arbitrary elements x1, x2) are:

  • Empty relation
    E = ∅;
    that is, x1Ex2 holds never;
  • Universal relation
    U = X × X;
    that is, x1Ux2 holds always;
  • Identity relation (see also identity function)
    I = {(x, x) | x ∈ X};
    that is, x1Ix2 holds if and only if x1 = x2.

Example

Plates tect2 en.svg

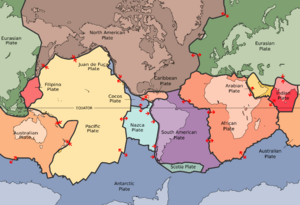
Fifteen large tectonic plates of the Earth's crust contact each other in a homogeneous relation. The relation can be expressed as a logical matrix with 1 indicating contact and 0 no contact. This example expresses a symmetric relation.

Properties

Some important properties that a homogeneous relation R over a set X may have are:

Reflexive
for all x ∈ X, xRx. For example, ≥ is a reflexive relation but > is not.
Irreflexive (or strict)
for all x ∈ X, not xRx. For example, > is an irreflexive relation, but ≥ is not.
Coreflexive
for all x, y ∈ X, if xRy then x = y.[7] For example, the relation over the integers in which each odd number is related to itself is a coreflexive relation. The equality relation is the only example of a both reflexive and coreflexive relation, and any coreflexive relation is a subset of the identity relation.
Left quasi-reflexive
for all x, y ∈ X, if xRy then xRx.
Right quasi-reflexive
for all x, y ∈ X, if xRy then yRy.
Quasi-reflexive
for all x, y ∈ X, if xRy then xRx and yRy. A relation is quasi-reflexive if, and only if, it is both left and right quasi-reflexive.

The previous 6 alternatives are far from being exhaustive; e.g., the red binary relation y = x2 is neither irreflexive, nor coreflexive, nor reflexive, since it contains the pair (0, 0), and (2, 4), but not (2, 2), respectively. The latter two facts also rule out (any kind of) quasi-reflexivity.

Symmetric
for all x, y ∈ X, if xRy then yRx. For example, "is a blood relative of" is a symmetric relation, because x is a blood relative of y if and only if y is a blood relative of x.
Antisymmetric
for all x, y ∈ X, if xRy and yRx then x = y. For example, ≥ is an antisymmetric relation; so is >, but vacuously (the condition in the definition is always false).[8]
Asymmetric
for all x, y ∈ X, if xRy then not yRx. A relation is asymmetric if and only if it is both antisymmetric and irreflexive.[9] For example, > is an asymmetric relation, but ≥ is not.

Again, the previous 3 alternatives are far from being exhaustive; as an example over the natural numbers, the relation xRy defined by x > 2 is neither symmetric nor antisymmetric, let alone asymmetric.

Transitive
for all x, y, z ∈ X, if xRy and yRz then xRz. A transitive relation is irreflexive if and only if it is asymmetric.[10] For example, "is ancestor of" is a transitive relation, while "is parent of" is not.
Antitransitive
for all x, y, z ∈ X, if xRy and yRz then never xRz.
Co-transitive
if the complement of R is transitive. That is, for all x, y, z ∈ X, if xRz, then xRy or yRz. This is used in pseudo-orders in constructive mathematics.
Quasitransitive
for all x, y, z ∈ X, if xRy and yRz but neither yRx nor zRy, then xRz but not zRx.
Transitivity of incomparability
for all x, y, z ∈ X, if x and y are incomparable with respect to R and if the same is true of y and z, then x and z are also incomparable with respect to R. This is used in weak orderings.

Again, the previous 5 alternatives are not exhaustive. For example, the relation xRy if (y = 0 or y = x+1) satisfies none of these properties. On the other hand, the empty relation trivially satisfies all of them.

Dense
for all x, y ∈ X such that xRy, there exists some z ∈ X such that xRz and zRy. This is used in dense orders.
Connected
for all x, y ∈ X, if x ≠ y then xRy or yRx. This property is sometimes called "total", which is distinct from the definitions of "left/right-total" given below.
Strongly connected
for all x, y ∈ X, xRy or yRx. This property, too, is sometimes called "total", which is distinct from the definitions of "left/right-total" given below.
Trichotomous
for all x, y ∈ X, exactly one of xRy, yRx or x = y holds. For example, > is a trichotomous relation, while the relation "divides" over the natural numbers is not.[11]
Right Euclidean (or just Euclidean)
for all x, y, z ∈ X, if xRy and xRz then yRz. For example, = is a Euclidean relation because if x = y and x = z then y = z.
Left Euclidean
for all x, y, z ∈ X, if yRx and zRx then yRz.
Well-founded
every nonempty subset S of X contains a minimal element with respect to R. Well-foundedness implies the descending chain condition (that is, no infinite chain ... xnR...Rx3Rx2Rx1 can exist). If the axiom of dependent choice is assumed, both conditions are equivalent.[12][13]

Moreover, all properties of binary relations in general also may apply to homogeneous relations:

Set-like
for all x ∈ X, the class of all y such that yRx is a set. (This makes sense only if relations over proper classes are allowed.)
Left-unique
for all x, z ∈ X and all y ∈ Y, if xRy and zRy then x = z.
Univalent
for all x ∈ X and all y, z ∈ Y, if xRy and xRz then y = z.[14]
Surjective (also called right-total)
for all y ∈ Y, there exists an x ∈ X such that xRy.

A preorder is a relation that is reflexive and transitive. A total preorder, also called linear preorder or weak order, is a relation that is reflexive, transitive, and connected.

A partial order, also called order, is a relation that is reflexive, antisymmetric, and transitive. A strict partial order, also called strict order, , also called linear order, simple order, or chain, is a relation that is reflexive, antisymmetric, transitive and connected.[15] A strict total order, also called strict linear order, strict simple order, or strict chain, is a relation that is irreflexive, antisymmetric, transitive and connected.

A partial equivalence relation is a relation that is symmetric and transitive. An equivalence relation is a relation that is reflexive, symmetric, and transitive. It is also a relation that is symmetric, transitive, and total, since these properties imply reflexivity.

Implications and conflicts between properties of homogeneous binary relations
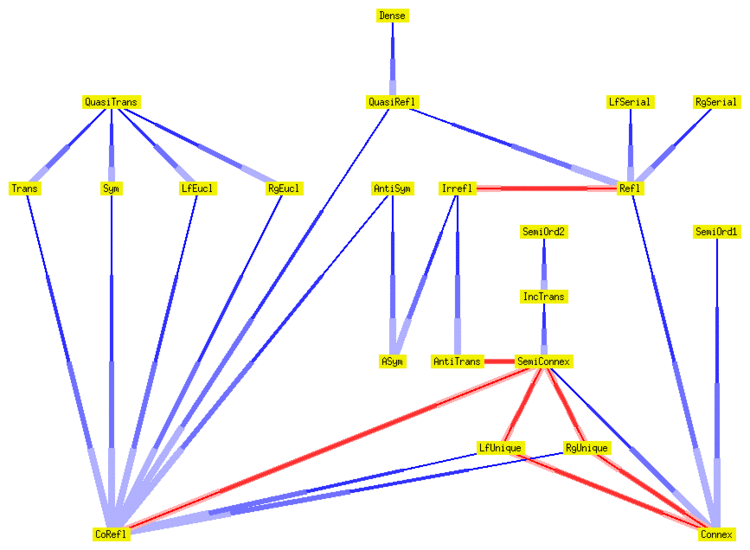Implications (blue) and conflicts (red) between properties (yellow) of homogeneous binary relations. For example, every asymmetric relation is irreflexive ("ASym ⇒ Irrefl"), and no relation on a non-empty set can be both irreflexive and reflexive ("Irrefl # Refl"). Omitting the red edges results in a Hasse diagram.

Operations

If R is a homogeneous relation over a set X then each of the following is a homogeneous relation over X:

Reflexive closure, R=
Defined as R= = {(x, x) | x ∈ X} ∪ R or the smallest reflexive relation over X containing R. This can be proven to be equal to the intersection of all reflexive relations containing R.
Reflexive reduction, R≠
Defined as R≠ = R \ {(x, x) | x ∈ X} or the largest irreflexive relation over X contained in R.
Transitive closure, R+
Defined as the smallest transitive relation over X containing R. This can be seen to be equal to the intersection of all transitive relations containing R.
Reflexive transitive closure, R*
Defined as R* = (R+)=, the smallest preorder containing R.
Reflexive transitive symmetric closure, R≡
Defined as the smallest equivalence relation over X containing R.

All operations defined in Binary relation § Operations also apply to homogeneous relations.

Homogeneous relations by property
Reflexivity Symmetry Transitivity Connectedness Symbol Example
Directed graph →
Undirected graph Symmetric
Dependency Reflexive Symmetric
Tournament Irreflexive Asymmetric Pecking order
Preorder Reflexive Transitive ≤ Preference
Total preorder Reflexive Transitive Connected ≤
Partial order Reflexive Antisymmetric Transitive ≤ Subset
Strict partial order Irreflexive Asymmetric Transitive < Strict subset
Total order Reflexive Antisymmetric Transitive Connected ≤ Alphabetical order
Strict total order Irreflexive Asymmetric Transitive Connected < Strict alphabetical order
Partial equivalence relation Symmetric Transitive
Equivalence relation Reflexive Symmetric Transitive ∼, ≡ Equality

Enumeration

The set of all homogeneous relations [math]\displaystyle{ \mathcal{B}(X) }[/math] over a set X is the set 2X × X which is a Boolean algebra augmented with the involution of mapping of a relation to its converse relation. Considering composition of relations as a binary operation on [math]\displaystyle{ \mathcal{B}(X) }[/math], it forms a monoid with involution where the identity element is the identity relation.[16]

The number of distinct homogeneous relations over an n-element set is 2n2 (sequence A002416 in the OEIS):

Number of n-element binary relations of different types
Elem­ents Any Transitive Reflexive Preorder Partial order Total preorder Total order Equivalence relation
0 1 1 1 1 1 1 1 1
1 2 2 1 1 1 1 1 1
2 16 13 4 4 3 3 2 2
3 512 171 64 29 19 13 6 5
4 65,536 3,994 4,096 355 219 75 24 15
n 2n2 2n2−n ∑n
k=0  k! S(n, k) 		n! ∑n
k=0  S(n, k)
OEIS A002416 A006905 A053763 A000798 A001035 A000670 A000142 A000110

Notes:

  • The number of irreflexive relations is the same as that of reflexive relations.
  • The number of strict partial orders (irreflexive transitive relations) is the same as that of partial orders.
  • The number of strict weak orders is the same as that of total preorders.
  • The total orders are the partial orders that are also total preorders. The number of preorders that are neither a partial order nor a total preorder is, therefore, the number of preorders, minus the number of partial orders, minus the number of total preorders, plus the number of total orders: 0, 0, 0, 3, and 85, respectively.
  • The number of equivalence relations is the number of partitions, which is the Bell number.

The homogeneous relations can be grouped into pairs (relation, complement), except that for n = 0 the relation is its own complement. The non-symmetric ones can be grouped into quadruples (relation, complement, inverse, inverse complement).

Examples

Generalizations

  • A binary relation in general need not be homogeneous, it is defined to be a subset R ⊆ X × Y for arbitrary sets X and Y.
  • A finitary relation is a subset R ⊆ X1 × ... × Xn for some natural number n and arbitrary sets X1, ..., Xn, it is also called an n-ary relation.

References

  1. ↑ Michael Winter (2007). Goguen Categories: A Categorical Approach to L-fuzzy Relations. Springer. pp. x-xi. ISBN 978-1-4020-6164-6. 
  2. ↑ M. E. Müller (2012). Relational Knowledge Discovery. Cambridge University Press. p. 22. ISBN 978-0-521-19021-3. 
  3. ↑ Peter J. Pahl; Rudolf Damrath (2001). Mathematical Foundations of Computational Engineering: A Handbook. Springer Science & Business Media. p. 496. ISBN 978-3-540-67995-0. 
  4. ↑ Mordeson, John N.; Nair, Premchand S. (8 November 2012) (in en). Fuzzy Mathematics: An Introduction for Engineers and Scientists. Physica. p. 2. ISBN 978-3-7908-1808-6. https://books.google.com/books?id=KfLwCAAAQBAJ&pg=PA2. 
  5. ↑ Tanaev, V.; Gordon, W.; Shafransky, Yakov M. (6 December 2012) (in en). Scheduling Theory. Single-Stage Systems. Springer Science & Business Media. p. 41. ISBN 978-94-011-1190-4. https://books.google.com/books?id=ITDyCAAAQBAJ&pg=PA41. 
  6. ↑ Meyer, Bertrand (29 June 2009) (in en). Touch of Class: Learning to Program Well with Objects and Contracts. Springer Science & Business Media. p. 509. ISBN 978-3-540-92145-5. https://books.google.com/books?id=AYNKAAAAQBAJ&pg=PA509. 
  7. ↑ Fonseca de Oliveira, J. N., & Pereira Cunha Rodrigues, C. D. J. (2004). Transposing Relations: From Maybe Functions to Hash Tables. In Mathematics of Program Construction (p. 337).
  8. ↑ Smith, Douglas; Eggen, Maurice; St. Andre, Richard (2006), A Transition to Advanced Mathematics (6th ed.), Brooks/Cole, p. 160, ISBN 0-534-39900-2 
  9. ↑ Nievergelt, Yves (2002), Foundations of Logic and Mathematics: Applications to Computer Science and Cryptography, Springer-Verlag, p. 158 .
  10. ↑ Flaška, V.; Ježek, J.; Kepka, T.; Kortelainen, J. (2007). Transitive Closures of Binary Relations I. Prague: School of Mathematics – Physics Charles University. p. 1. http://www.karlin.mff.cuni.cz/~jezek/120/transitive1.pdf.  Lemma 1.1 (iv). This source refers to asymmetric relations as "strictly antisymmetric".
  11. ↑ Since neither 5 divides 3, nor 3 divides 5, nor 3=5.
  12. ↑ "Condition for Well-Foundedness". https://proofwiki.org/wiki/Condition_for_Well-Foundedness. 
  13. ↑ Fraisse, R. (15 December 2000). Theory of Relations, Volume 145 - 1st Edition (1st ed.). Elsevier. p. 46. ISBN 9780444505422. https://www.elsevier.com/books/theory-of-relations/fraisse/978-0-444-50542-2. Retrieved 20 February 2019. 
  14. ↑ Gunther Schmidt & Thomas Strohlein (2012)[1987] Relations and Graphs, p. 54, at Google Books
  15. ↑ Joseph G. Rosenstein, Linear orderings, Academic Press, 1982, ISBN:0-12-597680-1, p. 4
  16. ↑ Schmidt, Gunther; Ströhlein, Thomas (1993). "Homogeneous Relations" (in en). Relations and Graphs: Discrete Mathematics for Computer Scientists. Berlin, Heidelberg: Springer. p. 14. doi:10.1007/978-3-642-77968-8_2. ISBN 978-3-642-77968-8. https://link.springer.com/chapter/10.1007/978-3-642-77968-8_2. 




Retrieved from "https://handwiki.org/wiki/index.php?title=Homogeneous_relation&oldid=3384444"