Symmetric relation

A symmetric relation is a type of binary relation. An example is the relation "is equal to", because if a = b is true then b = a is also true. Formally, a binary relation R over a set X is symmetric if:

[math]\displaystyle{ \forall a, b \in X(a R b \Leftrightarrow b R a) , }[/math]

where the notation aRb means that (a, b) ∈ R.

If R^T represents the converse of R, then R is symmetric if and only if R = R^T.

Symmetry, along with reflexivity and transitivity, are the three defining properties of an equivalence relation.

Examples

In mathematics

• "is equal to" (equality) (whereas "is less than" is not symmetric)
• "is comparable to", for elements of a partially ordered set
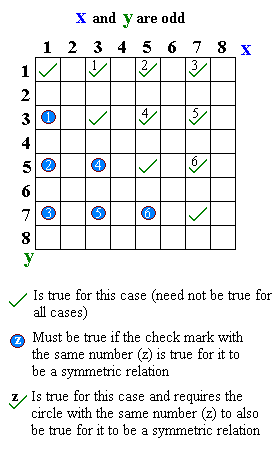
• "... and ... are odd":

Outside mathematics

• "is married to" (in most legal systems)
• "is a fully biological sibling of"
• "is a homophone of"
• "is co-worker of"
• "is teammate of"

Relationship to asymmetric and antisymmetric relations

Symmetric and antisymmetric relations

By definition, a nonempty relation cannot be both symmetric and asymmetric (where if a is related to b, then b cannot be related to a (in the same way)). However, a relation can be neither symmetric nor asymmetric, which is the case for "is less than or equal to" and "preys on").

Symmetric and antisymmetric (where the only way a can be related to b and b be related to a is if a = b) are actually independent of each other, as these examples show.

Mathematical examples

	Symmetric	Not symmetric
Antisymmetric	equality	divides, less than or equal to
Not antisymmetric	congruence in modular arithmetic	// (integer division), most nontrivial permutations

Non-mathematical examples

	Symmetric	Not symmetric
Antisymmetric	is the same person as, and is married	is the plural of
Not antisymmetric	is a full biological sibling of	preys on

Properties

• A symmetric and transitive relation is always quasireflexive.
• A symmetric, transitive, and reflexive relation is called an equivalence relation.
• One way to count the symmetric relations on n elements, that in their binary matrix representation the upper right triangle determines the relation fully, and it can be arbitrary given, thus there are as many symmetric relations as n × n binary upper triangle matrices, 2^n(n+1)/2.

Number of n-element binary relations of different types

Elem­ents	Any	Transitive	Reflexive	Preorder	Partial order	Total preorder	Total order	Equivalence relation
0	1	1	1	1	1	1	1	1
1	2	2	1	1	1	1	1	1
2	16	13	4	4	3	3	2	2
3	512	171	64	29	19	13	6	5
4	65,536	3,994	4,096	355	219	75	24	15
n	2n2		2n2−n			∑n k=0  k! S(n, k)	n!	∑n k=0  S(n, k)
OEIS	A002416	A006905	A053763	A000798	A001035	A000670	A000142	A000110

See also

• Commutative property – Property of some mathematical operations
• Symmetry in mathematics
• Symmetry – Mathematical invariance under transformations