Initial topology

Short description: Coarsest topology making certain functions continuous

In general topology and related areas of mathematics, the initial topology (or induced topology or weak topology or limit topology or projective topology) on a set [math]\displaystyle{ X, }[/math] with respect to a family of functions on [math]\displaystyle{ X, }[/math] is the coarsest topology on [math]\displaystyle{ X }[/math] that makes those functions continuous.

The subspace topology and product topology constructions are both special cases of initial topologies. Indeed, the initial topology construction can be viewed as a generalization of these.

The dual notion is the final topology, which for a given family of functions mapping to a set [math]\displaystyle{ X }[/math] is the finest topology on [math]\displaystyle{ X }[/math] that makes those functions continuous.

Definition

Given a set [math]\displaystyle{ X }[/math] and an indexed family [math]\displaystyle{ \left(Y_i\right)_{i \in I} }[/math] of topological spaces with functions [math]\displaystyle{ f_i : X \to Y_i, }[/math] the initial topology [math]\displaystyle{ \tau }[/math] on [math]\displaystyle{ X }[/math] is the coarsest topology on [math]\displaystyle{ X }[/math] such that each [math]\displaystyle{ f_i : (X, \tau) \to Y_i }[/math] is continuous.

Definition in terms of open sets

If [math]\displaystyle{ \left(\tau_i\right)_{i \in I} }[/math] is a family of topologies [math]\displaystyle{ X }[/math] indexed by [math]\displaystyle{ I \neq \varnothing, }[/math] then the least upper bound topology of these topologies is the coarsest topology on [math]\displaystyle{ X }[/math] that is finer than each [math]\displaystyle{ \tau_i. }[/math] This topology always exists and it is equal to the topology generated by [math]\displaystyle{ {\textstyle \bigcup\limits_{i \in I} \tau_i}. }[/math]

If for every [math]\displaystyle{ i \in I, }[/math] [math]\displaystyle{ \sigma_i }[/math] denotes the topology on [math]\displaystyle{ Y_i, }[/math] then [math]\displaystyle{ f_i^{-1}\left(\sigma_i\right) = \left\{f_i^{-1}(V) : V \in \sigma_i\right\} }[/math] is a topology on [math]\displaystyle{ X }[/math], and the initial topology of the [math]\displaystyle{ Y_i }[/math] by the mappings [math]\displaystyle{ f_i }[/math] is the least upper bound topology of the [math]\displaystyle{ I }[/math]-indexed family of topologies [math]\displaystyle{ f_i^{-1}\left(\sigma_i\right) }[/math] (for [math]\displaystyle{ i \in I }[/math]). Explicitly, the initial topology is the collection of open sets generated by all sets of the form [math]\displaystyle{ f_i^{-1}(U), }[/math] where [math]\displaystyle{ U }[/math] is an open set in [math]\displaystyle{ Y_i }[/math] for some [math]\displaystyle{ i \in I, }[/math] under finite intersections and arbitrary unions.

Sets of the form [math]\displaystyle{ f_i^{-1}(V) }[/math] are often called cylinder sets. If [math]\displaystyle{ I }[/math] contains exactly one element, then all the open sets of the initial topology [math]\displaystyle{ (X, \tau) }[/math] are cylinder sets.

Examples

Several topological constructions can be regarded as special cases of the initial topology.

• The subspace topology is the initial topology on the subspace with respect to the inclusion map.
• The product topology is the initial topology with respect to the family of projection maps.
• The inverse limit of any inverse system of spaces and continuous maps is the set-theoretic inverse limit together with the initial topology determined by the canonical morphisms.
• The weak topology on a locally convex space is the initial topology with respect to the continuous linear forms of its dual space.
• Given a family of topologies [math]\displaystyle{ \left\{\tau_i\right\} }[/math] on a fixed set [math]\displaystyle{ X }[/math] the initial topology on [math]\displaystyle{ X }[/math] with respect to the functions [math]\displaystyle{ \operatorname{id}_i : X \to \left(X, \tau_i\right) }[/math] is the supremum (or join) of the topologies [math]\displaystyle{ \left\{\tau_i\right\} }[/math] in the lattice of topologies on [math]\displaystyle{ X. }[/math] That is, the initial topology [math]\displaystyle{ \tau }[/math] is the topology generated by the union of the topologies [math]\displaystyle{ \left\{\tau_i\right\}. }[/math]
• A topological space is completely regular if and only if it has the initial topology with respect to its family of (bounded) real-valued continuous functions.
• Every topological space [math]\displaystyle{ X }[/math] has the initial topology with respect to the family of continuous functions from [math]\displaystyle{ X }[/math] to the Sierpiński space.

Properties

Characteristic property

The initial topology on [math]\displaystyle{ X }[/math] can be characterized by the following characteristic property:
A function [math]\displaystyle{ g }[/math] from some space [math]\displaystyle{ Z }[/math] to [math]\displaystyle{ X }[/math] is continuous if and only if [math]\displaystyle{ f_i \circ g }[/math] is continuous for each [math]\displaystyle{ i \in I. }[/math]

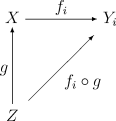
Note that, despite looking quite similar, this is not a universal property. A categorical description is given below.

A filter [math]\displaystyle{ \mathcal{B} }[/math] on [math]\displaystyle{ X }[/math] converges to a point [math]\displaystyle{ x \in X }[/math] if and only if the prefilter [math]\displaystyle{ f_i(\mathcal{B}) }[/math] converges to [math]\displaystyle{ f_i(x) }[/math] for every [math]\displaystyle{ i \in I. }[/math]

Evaluation

By the universal property of the product topology, we know that any family of continuous maps [math]\displaystyle{ f_i : X \to Y_i }[/math] determines a unique continuous map [math]\displaystyle{ \begin{alignat}{4} f :\;&& X &&\;\to \;& \prod_i Y_i \\[0.3ex] && x &&\;\mapsto\;& \left(f_i(x)\right)_{i \in I} \\ \end{alignat} }[/math]

This map is known as the evaluation map.

A family of maps [math]\displaystyle{ \{f_i : X \to Y_i\} }[/math] is said to separate points in [math]\displaystyle{ X }[/math] if for all [math]\displaystyle{ x \neq y }[/math] in [math]\displaystyle{ X }[/math] there exists some [math]\displaystyle{ i }[/math] such that [math]\displaystyle{ f_i(x) \neq f_i(y). }[/math] The family [math]\displaystyle{ \{f_i\} }[/math] separates points if and only if the associated evaluation map [math]\displaystyle{ f }[/math] is injective.

The evaluation map [math]\displaystyle{ f }[/math] will be a topological embedding if and only if [math]\displaystyle{ X }[/math] has the initial topology determined by the maps [math]\displaystyle{ \{f_i\} }[/math] and this family of maps separates points in [math]\displaystyle{ X. }[/math]

Hausdorffness

If [math]\displaystyle{ X }[/math] has the initial topology induced by [math]\displaystyle{ \left\{f_i : X \to Y_i\right\} }[/math] and if every [math]\displaystyle{ Y_i }[/math] is Hausdorff, then [math]\displaystyle{ X }[/math] is a Hausdorff space if and only if these maps separate points on [math]\displaystyle{ X. }[/math]

Transitivity of the initial topology

If [math]\displaystyle{ X }[/math] has the initial topology induced by the [math]\displaystyle{ I }[/math]-indexed family of mappings [math]\displaystyle{ \left\{f_i : X \to Y_i\right\} }[/math] and if for every [math]\displaystyle{ i \in I, }[/math] the topology on [math]\displaystyle{ Y_i }[/math] is the initial topology induced by some [math]\displaystyle{ J_i }[/math]-indexed family of mappings [math]\displaystyle{ \left\{g_j : Y_i \to Z_j\right\} }[/math] (as [math]\displaystyle{ j }[/math] ranges over [math]\displaystyle{ J_i }[/math]), then the initial topology on [math]\displaystyle{ X }[/math] induced by [math]\displaystyle{ \left\{f_i : X \to Y_i\right\} }[/math] is equal to the initial topology induced by the [math]\displaystyle{ {\textstyle \bigcup\limits_{i \in I} J_i} }[/math]-indexed family of mappings [math]\displaystyle{ \left\{g_j \circ f_i : X \to Z_j\right\} }[/math] as [math]\displaystyle{ i }[/math] ranges over [math]\displaystyle{ I }[/math] and [math]\displaystyle{ j }[/math] ranges over [math]\displaystyle{ J_i. }[/math] Several important corollaries of this fact are now given.

In particular, if [math]\displaystyle{ S \subseteq X }[/math] then the subspace topology that [math]\displaystyle{ S }[/math] inherits from [math]\displaystyle{ X }[/math] is equal to the initial topology induced by the inclusion map [math]\displaystyle{ S \to X }[/math] (defined by [math]\displaystyle{ s \mapsto s }[/math]). Consequently, if [math]\displaystyle{ X }[/math] has the initial topology induced by [math]\displaystyle{ \left\{f_i : X \to Y_i\right\} }[/math] then the subspace topology that [math]\displaystyle{ S }[/math] inherits from [math]\displaystyle{ X }[/math] is equal to the initial topology induced on [math]\displaystyle{ S }[/math] by the restrictions [math]\displaystyle{ \left\{\left.f_i\right|_S : S \to Y_i\right\} }[/math] of the [math]\displaystyle{ f_i }[/math] to [math]\displaystyle{ S. }[/math]

The product topology on [math]\displaystyle{ \prod_i Y_i }[/math] is equal to the initial topology induced by the canonical projections [math]\displaystyle{ \operatorname{pr}_i : \left(x_k\right)_{k \in I} \mapsto x_i }[/math] as [math]\displaystyle{ i }[/math] ranges over [math]\displaystyle{ I. }[/math] Consequently, the initial topology on [math]\displaystyle{ X }[/math] induced by [math]\displaystyle{ \left\{f_i : X \to Y_i\right\} }[/math] is equal to the inverse image of the product topology on [math]\displaystyle{ \prod_i Y_i }[/math] by the evaluation map [math]\displaystyle{ f : X \to \prod_i Y_i\,. }[/math] Furthermore, if the maps [math]\displaystyle{ \left\{f_i\right\}_{i \in I} }[/math] separate points on [math]\displaystyle{ X }[/math] then the evaluation map is a homeomorphism onto the subspace [math]\displaystyle{ f(X) }[/math] of the product space [math]\displaystyle{ \prod_i Y_i. }[/math]

Separating points from closed sets

If a space [math]\displaystyle{ X }[/math] comes equipped with a topology, it is often useful to know whether or not the topology on [math]\displaystyle{ X }[/math] is the initial topology induced by some family of maps on [math]\displaystyle{ X. }[/math] This section gives a sufficient (but not necessary) condition.

A family of maps [math]\displaystyle{ \left\{f_i : X \to Y_i\right\} }[/math] separates points from closed sets in [math]\displaystyle{ X }[/math] if for all closed sets [math]\displaystyle{ A }[/math] in [math]\displaystyle{ X }[/math] and all [math]\displaystyle{ x \not\in A, }[/math] there exists some [math]\displaystyle{ i }[/math] such that [math]\displaystyle{ f_i(x) \notin \operatorname{cl}(f_i(A)) }[/math] where [math]\displaystyle{ \operatorname{cl} }[/math] denotes the closure operator.

Theorem. A family of continuous maps [math]\displaystyle{ \left\{f_i : X \to Y_i\right\} }[/math] separates points from closed sets if and only if the cylinder sets [math]\displaystyle{ f_i^{-1}(V), }[/math] for [math]\displaystyle{ V }[/math] open in [math]\displaystyle{ Y_i, }[/math] form a base for the topology on [math]\displaystyle{ X. }[/math]

It follows that whenever [math]\displaystyle{ \left\{f_i\right\} }[/math] separates points from closed sets, the space [math]\displaystyle{ X }[/math] has the initial topology induced by the maps [math]\displaystyle{ \left\{f_i\right\}. }[/math] The converse fails, since generally the cylinder sets will only form a subbase (and not a base) for the initial topology.

If the space [math]\displaystyle{ X }[/math] is a T₀ space, then any collection of maps [math]\displaystyle{ \left\{f_i\right\} }[/math] that separates points from closed sets in [math]\displaystyle{ X }[/math] must also separate points. In this case, the evaluation map will be an embedding.

Initial uniform structure

If [math]\displaystyle{ \left(\mathcal{U}_i\right)_{i \in I} }[/math] is a family of uniform structures on [math]\displaystyle{ X }[/math] indexed by [math]\displaystyle{ I \neq \varnothing, }[/math] then the least upper bound uniform structure of [math]\displaystyle{ \left(\mathcal{U}_i\right)_{i \in I} }[/math] is the coarsest uniform structure on [math]\displaystyle{ X }[/math] that is finer than each [math]\displaystyle{ \mathcal{U}_i. }[/math] This uniform always exists and it is equal to the filter on [math]\displaystyle{ X \times X }[/math] generated by the filter subbase [math]\displaystyle{ {\textstyle \bigcup\limits_{i \in I} \mathcal{U}_i}. }[/math] If [math]\displaystyle{ \tau_i }[/math] is the topology on [math]\displaystyle{ X }[/math] induced by the uniform structure [math]\displaystyle{ \mathcal{U}_i }[/math] then the topology on [math]\displaystyle{ X }[/math] associated with least upper bound uniform structure is equal to the least upper bound topology of [math]\displaystyle{ \left(\tau_i\right)_{i \in I}. }[/math]

Now suppose that [math]\displaystyle{ \left\{f_i : X \to Y_i\right\} }[/math] is a family of maps and for every [math]\displaystyle{ i \in I, }[/math] let [math]\displaystyle{ \mathcal{U}_i }[/math] be a uniform structure on [math]\displaystyle{ Y_i. }[/math] Then the initial uniform structure of the [math]\displaystyle{ Y_i }[/math] by the mappings [math]\displaystyle{ f_i }[/math] is the unique coarsest uniform structure [math]\displaystyle{ \mathcal{U} }[/math] on [math]\displaystyle{ X }[/math] making all [math]\displaystyle{ f_i : \left(X, \mathcal{U}\right) \to \left(Y_i, \mathcal{U}_i\right) }[/math] uniformly continuous. It is equal to the least upper bound uniform structure of the [math]\displaystyle{ I }[/math]-indexed family of uniform structures [math]\displaystyle{ f_i^{-1}\left(\mathcal{U}_i\right) }[/math] (for [math]\displaystyle{ i \in I }[/math]). The topology on [math]\displaystyle{ X }[/math] induced by [math]\displaystyle{ \mathcal{U} }[/math] is the coarsest topology on [math]\displaystyle{ X }[/math] such that every [math]\displaystyle{ f_i : X \to Y_i }[/math] is continuous. The initial uniform structure [math]\displaystyle{ \mathcal{U} }[/math] is also equal to the coarsest uniform structure such that the identity mappings [math]\displaystyle{ \operatorname{id} : \left(X, \mathcal{U}\right) \to \left(X, f_i^{-1}\left(\mathcal{U}_i\right)\right) }[/math] are uniformly continuous.

Hausdorffness: The topology on [math]\displaystyle{ X }[/math] induced by the initial uniform structure [math]\displaystyle{ \mathcal{U} }[/math] is Hausdorff if and only if for whenever [math]\displaystyle{ x, y \in X }[/math] are distinct ([math]\displaystyle{ x \neq y }[/math]) then there exists some [math]\displaystyle{ i \in I }[/math] and some entourage [math]\displaystyle{ V_i \in \mathcal{U}_i }[/math] of [math]\displaystyle{ Y_i }[/math] such that [math]\displaystyle{ \left(f_i(x), f_i(y)\right) \not\in V_i. }[/math] Furthermore, if for every index [math]\displaystyle{ i \in I, }[/math] the topology on [math]\displaystyle{ Y_i }[/math] induced by [math]\displaystyle{ \mathcal{U}_i }[/math] is Hausdorff then the topology on [math]\displaystyle{ X }[/math] induced by the initial uniform structure [math]\displaystyle{ \mathcal{U} }[/math] is Hausdorff if and only if the maps [math]\displaystyle{ \left\{f_i : X \to Y_i\right\} }[/math] separate points on [math]\displaystyle{ X }[/math] (or equivalently, if and only if the evaluation map [math]\displaystyle{ f : X \to \prod_i Y_i }[/math] is injective)

Uniform continuity: If [math]\displaystyle{ \mathcal{U} }[/math] is the initial uniform structure induced by the mappings [math]\displaystyle{ \left\{f_i : X \to Y_i\right\}, }[/math] then a function [math]\displaystyle{ g }[/math] from some uniform space [math]\displaystyle{ Z }[/math] into [math]\displaystyle{ (X, \mathcal{U}) }[/math] is uniformly continuous if and only if [math]\displaystyle{ f_i \circ g : Z \to Y_i }[/math] is uniformly continuous for each [math]\displaystyle{ i \in I. }[/math]

Cauchy filter: A filter [math]\displaystyle{ \mathcal{B} }[/math] on [math]\displaystyle{ X }[/math] is a Cauchy filter on [math]\displaystyle{ (X, \mathcal{U}) }[/math] if and only if [math]\displaystyle{ f_i\left(\mathcal{B}\right) }[/math] is a Cauchy prefilter on [math]\displaystyle{ Y_i }[/math] for every [math]\displaystyle{ i \in I. }[/math]

Transitivity of the initial uniform structure: If the word "topology" is replaced with "uniform structure" in the statement of "transitivity of the initial topology" given above, then the resulting statement will also be true.

Categorical description

In the language of category theory, the initial topology construction can be described as follows. Let [math]\displaystyle{ Y }[/math] be the functor from a discrete category [math]\displaystyle{ J }[/math] to the category of topological spaces [math]\displaystyle{ \mathrm{Top} }[/math] which maps [math]\displaystyle{ j\mapsto Y_j }[/math]. Let [math]\displaystyle{ U }[/math] be the usual forgetful functor from [math]\displaystyle{ \mathrm{Top} }[/math] to [math]\displaystyle{ \mathrm{Set} }[/math]. The maps [math]\displaystyle{ f_j : X \to Y_j }[/math] can then be thought of as a cone from [math]\displaystyle{ X }[/math] to [math]\displaystyle{ UY. }[/math] That is, [math]\displaystyle{ (X,f) }[/math] is an object of [math]\displaystyle{ \mathrm{Cone}(UY) := (\Delta\downarrow{UY}) }[/math]—the category of cones to [math]\displaystyle{ UY. }[/math] More precisely, this cone [math]\displaystyle{ (X,f) }[/math] defines a [math]\displaystyle{ U }[/math]-structured cosink in [math]\displaystyle{ \mathrm{Set}. }[/math]

The forgetful functor [math]\displaystyle{ U : \mathrm{Top} \to \mathrm{Set} }[/math] induces a functor [math]\displaystyle{ \bar{U} : \mathrm{Cone}(Y) \to \mathrm{Cone}(UY) }[/math]. The characteristic property of the initial topology is equivalent to the statement that there exists a universal morphism from [math]\displaystyle{ \bar{U} }[/math] to [math]\displaystyle{ (X,f); }[/math] that is, a terminal object in the category [math]\displaystyle{ \left(\bar{U}\downarrow(X,f)\right). }[/math]
Explicitly, this consists of an object [math]\displaystyle{ I(X,f) }[/math] in [math]\displaystyle{ \mathrm{Cone}(Y) }[/math] together with a morphism [math]\displaystyle{ \varepsilon : \bar{U} I(X,f) \to (X,f) }[/math] such that for any object [math]\displaystyle{ (Z,g) }[/math] in [math]\displaystyle{ \mathrm{Cone}(Y) }[/math] and morphism [math]\displaystyle{ \varphi : \bar{U}(Z,g) \to (X,f) }[/math] there exists a unique morphism [math]\displaystyle{ \zeta : (Z,g) \to I(X,f) }[/math] such that the following diagram commutes:

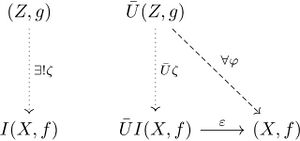
The assignment [math]\displaystyle{ (X,f) \mapsto I(X,f) }[/math] placing the initial topology on [math]\displaystyle{ X }[/math] extends to a functor [math]\displaystyle{ I : \mathrm{Cone}(UY) \to \mathrm{Cone}(Y) }[/math] which is right adjoint to the forgetful functor [math]\displaystyle{ \bar{U}. }[/math] In fact, [math]\displaystyle{ I }[/math] is a right-inverse to [math]\displaystyle{ \bar{U} }[/math]; since [math]\displaystyle{ \bar{U}I }[/math] is the identity functor on [math]\displaystyle{ \mathrm{Cone}(UY). }[/math]

See also

• Final topology – Finest topology making some functions continuous
• Product topology – Topology on Cartesian products of topological spaces
• Quotient space (topology) – Topological space construction
• Subspace topology – Inherited topology

Bibliography

• Bourbaki, Nicolas (1989). General Topology: Chapters 1–4. Éléments de mathématique. Berlin New York: Springer Science & Business Media. ISBN 978-3-540-64241-1. OCLC 18588129. https://doku.pub/documents/31425779-nicolas-bourbaki-general-topology-part-i1pdf-30j71z37920w. 
• Template:Bourbaki General Topology Part II Chapters 5-10
• Dugundji, James (1966). Topology. Boston: Allyn and Bacon. ISBN 978-0-697-06889-7. OCLC 395340485. 
• Grothendieck, Alexander (January 1, 1973). Topological Vector Spaces. New York: Gordon and Breach Science Publishers. ISBN 978-0-677-30020-7. OCLC 886098. https://archive.org/details/topologicalvecto0000grot. 
• Willard, Stephen (2004). General Topology. Dover Books on Mathematics (First ed.). Mineola, N.Y.: Dover Publications. ISBN 978-0-486-43479-7. OCLC 115240. 
• Willard, Stephen (1970). General Topology. Reading, Massachusetts: Addison-Wesley. ISBN 0-486-43479-6. https://archive.org/details/generaltopology00will_0. 

External links

• Initial topology at PlanetMath.org.
• Product topology and subspace topology at PlanetMath.org.