Johnson's SU-distribution
|
Probability density function  | |||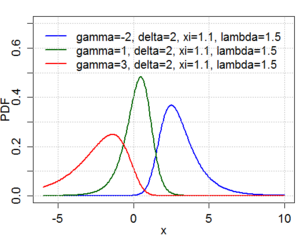
|
Cumulative distribution function  | |||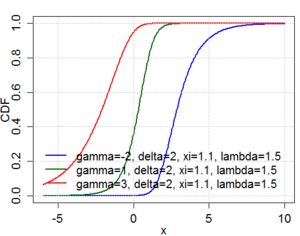
| Parameters | [math]\displaystyle{ \gamma, \xi, \delta \gt 0, \lambda \gt 0 }[/math] (real) | ||
|---|---|---|---|
| Support | [math]\displaystyle{ -\infty \text{ to } +\infty }[/math] | ||
| [math]\displaystyle{ \frac{\delta}{\lambda\sqrt{2\pi}} \frac{1}{\sqrt{1 + \left(\frac{x-\xi}{\lambda}\right)^2}} e^{-\frac{1}{2}\left(\gamma+\delta \sinh^{-1} \left(\frac{x-\xi}{\lambda}\right)\right)^2} }[/math] | |||
| CDF | [math]\displaystyle{ \Phi \left(\gamma + \delta \sinh^{-1} \left( \frac{x-\xi}{\lambda} \right) \right) }[/math] | ||
| Mean | [math]\displaystyle{ \xi - \lambda \exp \frac{\delta^{-2}}{2} \sinh\left(\frac{\gamma}{\delta}\right) }[/math] | ||
| Median | [math]\displaystyle{ \xi + \lambda \sinh \left( - \frac{\gamma}{\delta} \right) }[/math] | ||
| Variance | [math]\displaystyle{ \frac{\lambda^2}{2} (\exp(\delta^{-2})-1) \left( \exp(\delta^{-2}) \cosh \left(\frac{2\gamma}{\delta} \right) +1 \right) }[/math] | ||
| Skewness | [math]\displaystyle{ -\frac{\lambda^3\sqrt{e^{\delta^{-2}}}(e^{\delta^{-2}}-1)^{2}((e^{\delta^{-2}})(e^{\delta^{-2}}+2)\sinh(\frac{3\gamma}{\delta})+3\sinh(\frac{2\gamma}{\delta}))}{4(\operatorname{Variance}X)^{1.5}} }[/math] | ||
| Kurtosis |
[math]\displaystyle{ \frac{\lambda^4(e^{\delta^{-2}}-1)^2(K_{1}+K_2+K_3)}{8(\operatorname{Variance}X)^2} }[/math] [math]\displaystyle{ K_{1}=\left( e^{\delta^{-2}} \right)^{2}\left( \left( e^{\delta^{-2}} \right)^{4}+2\left( e^{\delta^{-2}} \right)^{3}+3\left( e^{\delta^{-2}} \right)^{2}-3 \right)\cosh\left( \frac{4\gamma}{\delta} \right) }[/math] [math]\displaystyle{ K_2=4\left( e^{\delta^{-2}} \right)^2 \left( \left( e^{\delta^{-2}} \right)+2 \right)\cosh\left( \frac{3\gamma}{\delta} \right) }[/math] [math]\displaystyle{ K_3=3\left( 2\left( e^{\delta^{-2}} \right)+1 \right) }[/math] | ||
The Johnson's SU-distribution is a four-parameter family of probability distributions first investigated by N. L. Johnson in 1949.[1][2] Johnson proposed it as a transformation of the normal distribution:[1]
- [math]\displaystyle{ z=\gamma+\delta \sinh^{-1} \left(\frac{x-\xi}{\lambda}\right) }[/math]
where [math]\displaystyle{ z \sim \mathcal{N}(0,1) }[/math].
Generation of random variables
Let U be a random variable that is uniformly distributed on the unit interval [0, 1]. Johnson's SU random variables can be generated from U as follows:
- [math]\displaystyle{ x = \lambda \sinh\left( \frac{ \Phi^{ -1 }( U ) - \gamma }{ \delta } \right) + \xi }[/math]
where Φ is the cumulative distribution function of the normal distribution.
Johnson's SB-distribution
N. L. Johnson[1] firstly proposes the transformation :
- [math]\displaystyle{ z=\gamma+\delta \log \left(\frac{x-\xi}{\xi+\lambda-x}\right) }[/math]
where [math]\displaystyle{ z \sim \mathcal{N}(0,1) }[/math].
Johnson's SB random variables can be generated from U as follows:
- [math]\displaystyle{ y={\left(1+{e}^{-\left(z-\gamma\right) /\delta }\right)}^{-1} }[/math]
- [math]\displaystyle{ x=\lambda y +\xi }[/math]
The SB-distribution is convenient to Platykurtic distributions (Kurtosis). To simulate SU, sample of code for its density and cumulative distribution function is available here
Applications
Johnson's [math]\displaystyle{ S_{U} }[/math]-distribution has been used successfully to model asset returns for portfolio management.[3] This comes as a superior alternative to using the Normal distribution to model asset returns. An R package, JSUparameters, was developed in 2021 to aid in the estimation of the parameters of the best-fitting Johnson's [math]\displaystyle{ S_{U} }[/math]-distribution for a given dataset. Johnson distributions are also sometimes used in option pricing, so as to accommodate an observed volatility smile; see Johnson binomial tree.
An alternative to the Johnson system of distributions is the quantile-parameterized distributions (QPDs). QPDs can provide greater shape flexibility than the Johnson system. Instead of fitting moments, QPDs are typically fit to empirical CDF data with linear least squares.
Johnson's [math]\displaystyle{ S_{U} }[/math]-distribution is also used in the modelling of the invariant mass of some heavy mesons in the field of B-physics.[4]
References
- ↑ 1.0 1.1 1.2 Johnson, N. L. (1949). "Systems of Frequency Curves Generated by Methods of Translation". Biometrika 36 (1/2): 149–176. doi:10.2307/2332539.
- ↑ Johnson, N. L. (1949). "Bivariate Distributions Based on Simple Translation Systems". Biometrika 36 (3/4): 297–304. doi:10.1093/biomet/36.3-4.297.
- ↑ Tsai, Cindy Sin-Yi (2011). "The Real World is Not Normal". Morningstar Alternative Investments Observer. http://morningstardirect.morningstar.com/clientcomm/iss/Tsai_Real_World_Not_Normal.pdf.
- ↑ As an example, see: LHCb Collaboration (2022). "Precise determination of the [math]\displaystyle{ {B}_{\mathrm{s}}^{0} }[/math]–[math]\displaystyle{ {\overline{B}}_{\mathrm{s}}^{0} }[/math] oscillation frequency". Nature Physics 18: 1-5. doi:10.1038/s41567-021-01394-x.
Further reading
- Hill, I. D.; Hill, R.; Holder, R. L. (1976). "Algorithm AS 99: Fitting Johnson Curves by Moments". Journal of the Royal Statistical Society. Series C (Applied Statistics) 25 (2).
- Jones, M. C.; Pewsey, A. (2009). "Sinh-arcsinh distributions". Biometrika 96 (4): 761. doi:10.1093/biomet/asp053. http://oro.open.ac.uk/22510/1/sinhasinh.pdf.( Preprint)
- Tuenter, Hans J. H. (November 2001). "An algorithm to determine the parameters of SU-curves in the Johnson system of probability distributions by moment matching". The Journal of Statistical Computation and Simulation 70 (4): 325–347. doi:10.1080/00949650108812126.
 |  |
