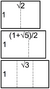
Natural logarithm of 2
From HandWiki
Short description: Mathematical constant
The decimal value of the natural logarithm of 2 (sequence A002162 in the OEIS) is approximately
- [math]\displaystyle{ \ln 2 \approx 0.693\,147\,180\,559\,945\,309\,417\,232\,121\,458. }[/math]
The logarithm of 2 in other bases is obtained with the formula
- [math]\displaystyle{ \log_b 2 = \frac{\ln 2}{\ln b}. }[/math]
The common logarithm in particular is (OEIS: A007524)
- [math]\displaystyle{ \log_{10} 2 \approx 0.301\,029\,995\,663\,981\,195. }[/math]
The inverse of this number is the binary logarithm of 10:
- [math]\displaystyle{ \log_2 10 =\frac{1}{\log_{10} 2} \approx 3.321\,928\,095 }[/math] (OEIS: A020862).
By the Lindemann–Weierstrass theorem, the natural logarithm of any natural number other than 0 and 1 (more generally, of any positive algebraic number other than 1) is a transcendental number.
Series representations
Rising alternate factorial
- [math]\displaystyle{ \ln 2 = \sum_{n=1}^\infty \frac{(-1)^{n+1}}{n}=1-\frac12+\frac13-\frac14+\frac15-\frac16+\cdots. }[/math] This is the well-known "alternating harmonic series".
- [math]\displaystyle{ \ln 2 = \frac{1}{2} +\frac{1}{2}\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n(n+1)}. }[/math]
- [math]\displaystyle{ \ln 2 = \frac{5}{8} +\frac{1}{2}\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n(n+1)(n+2)}. }[/math]
- [math]\displaystyle{ \ln 2 = \frac{2}{3} +\frac{3}{4}\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n(n+1)(n+2)(n+3)}. }[/math]
- [math]\displaystyle{ \ln 2 = \frac{131}{192} +\frac{3}{2}\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n(n+1)(n+2)(n+3)(n+4)}. }[/math]
- [math]\displaystyle{ \ln 2 = \frac{661}{960} +\frac{15}{4}\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n(n+1)(n+2)(n+3)(n+4)(n+5)}. }[/math]
- [math]\displaystyle{ \ln 2 = \frac{2}{3}.(1+\frac{2}{4^3-4}+\frac{2}{8^3-8}+\frac{2}{12^3-12}+.........) . }[/math]
Binary rising constant factorial
- [math]\displaystyle{ \ln 2 = \sum_{n=1}^\infty \frac{1}{2^{n}n}. }[/math]
- [math]\displaystyle{ \ln 2 = 1 -\sum_{n=1}^\infty \frac{1}{2^{n}n(n+1)}. }[/math]
- [math]\displaystyle{ \ln 2 = \frac{1}{2} + 2 \sum_{n=1}^\infty \frac{1}{2^{n}n(n+1)(n+2)} . }[/math]
- [math]\displaystyle{ \ln 2 = \frac{5}{6} - 6 \sum_{n=1}^\infty \frac{1}{2^{n}n(n+1)(n+2)(n+3)} . }[/math]
- [math]\displaystyle{ \ln 2 = \frac{7}{12} + 24 \sum_{n=1}^\infty \frac{1}{2^{n}n(n+1)(n+2)(n+3)(n+4)} . }[/math]
- [math]\displaystyle{ \ln 2 = \frac{47}{60} - 120 \sum_{n=1}^\infty \frac{1}{2^{n}n(n+1)(n+2)(n+3)(n+4)(n+5)} . }[/math]
Other series representations
- [math]\displaystyle{ \sum_{n=0}^\infty \frac{1}{(2n+1)(2n+2)} = \ln 2. }[/math]
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{n(4n^2-1)} = 2\ln 2 -1. }[/math]
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{(-1)^n}{n(4n^2-1)} = \ln 2 -1. }[/math]
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{(-1)^n}{n(9n^2-1)} = 2\ln 2 -\frac{3}{2}. }[/math]
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{4n^2-2n} = \ln 2. }[/math]
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{2(-1)^{n+1}(2n-1)+1}{8n^2-4n} = \ln 2. }[/math]
- [math]\displaystyle{ \sum_{n=0}^\infty \frac{(-1)^{n}}{3n+1} = \frac{\ln 2}{3}+\frac{\pi}{3\sqrt{3}}. }[/math]
- [math]\displaystyle{ \sum_{n=0}^\infty \frac{(-1)^{n}}{3n+2} = -\frac{\ln 2}{3}+\frac{\pi}{3\sqrt{3}}. }[/math]
- [math]\displaystyle{ \sum_{n=0}^\infty \frac{(-1)^{n}}{(3n+1)(3n+2)} = \frac{2\ln 2}{3}. }[/math]
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{\sum_{k=1}^n k^2} = 18 - 24 \ln 2 }[/math] using [math]\displaystyle{ \lim_{N\rightarrow \infty} \sum_{n=N}^{2N} \frac{1}{n} = \ln 2 }[/math]
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{4n^2-3n} = \ln 2 + \frac{\pi}{6} }[/math] (sums of the reciprocals of decagonal numbers)
Involving the Riemann Zeta function
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{n}[\zeta(2n)-1] = \ln 2. }[/math]
- [math]\displaystyle{ \sum_{n=2}^\infty \frac{1}{2^n}[\zeta(n)-1] = \ln 2 -\frac{1}{2}. }[/math]
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{2n+1}[\zeta(2n+1)-1] = 1-\gamma-\frac{\ln 2}{2}. }[/math]
- [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{2^{2n-1}(2n+1)}\zeta(2n) = 1-\ln 2. }[/math]
(γ is the Euler–Mascheroni constant and ζ Riemann's zeta function.)
BBP-type representations
- [math]\displaystyle{ \ln 2 = \frac{2}{3} + \frac{1}{2} \sum_{k = 1}^\infty \left(\frac{1}{2k}+\frac{1}{4k+1}+\frac{1}{8k+4}+\frac{1}{16k+12}\right) \frac{1}{16^k} . }[/math]
(See more about Bailey–Borwein–Plouffe (BBP)-type representations.)
Applying the three general series for natural logarithm to 2 directly gives:
- [math]\displaystyle{ \ln 2 = \sum_{n = 1}^\infty \frac{(-1)^{n-1}}{n}. }[/math]
- [math]\displaystyle{ \ln 2 = \sum_{n = 1}^\infty \frac{1}{2^{n}n}. }[/math]
- [math]\displaystyle{ \ln 2 = \frac{2}{3} \sum_{k = 0}^\infty \frac{1}{9^{k}(2k+1)}. }[/math]
Applying them to [math]\displaystyle{ \textstyle 2 = \frac{3}{2} \cdot \frac{4}{3} }[/math] gives:
- [math]\displaystyle{ \ln 2 = \sum_{n = 1}^\infty \frac{(-1)^{n-1}}{2^n n} + \sum_{n = 1}^\infty \frac{(-1)^{n-1}}{3^n n} . }[/math]
- [math]\displaystyle{ \ln 2 = \sum_{n = 1}^\infty \frac{1}{3^n n} + \sum_{n = 1}^\infty \frac{1}{4^n n} . }[/math]
- [math]\displaystyle{ \ln 2 = \frac{2}{5} \sum_{k = 0}^\infty \frac{1}{25^{k}(2k+1)} + \frac{2}{7} \sum_{k = 0}^\infty \frac{1}{49^{k}(2k+1)} . }[/math]
Applying them to [math]\displaystyle{ \textstyle 2 = (\sqrt{2})^2 }[/math] gives:
- [math]\displaystyle{ \ln 2 = 2 \sum_{n = 1}^\infty \frac{(-1)^{n-1}}{(\sqrt{2} + 1)^n n} . }[/math]
- [math]\displaystyle{ \ln 2 = 2 \sum_{n = 1}^\infty \frac{1}{(2 + \sqrt{2})^n n} . }[/math]
- [math]\displaystyle{ \ln 2 = \frac{4}{3 + 2 \sqrt{2}} \sum_{k = 0}^\infty \frac{1}{(17 + 12 \sqrt{2})^{k}(2k+1)} . }[/math]
Applying them to [math]\displaystyle{ \textstyle 2 = { \left( \frac{16}{15} \right) }^{7} \cdot { \left( \frac{81}{80} \right) }^{3} \cdot { \left( \frac{25}{24} \right) }^{5} }[/math] gives:
- [math]\displaystyle{ \ln 2 = 7 \sum_{n = 1}^\infty \frac{(-1)^{n-1}}{15^n n} + 3 \sum_{n = 1}^\infty \frac{(-1)^{n-1}}{80^n n} + 5 \sum_{n = 1}^\infty \frac{(-1)^{n-1}}{24^n n} . }[/math]
- [math]\displaystyle{ \ln 2 = 7 \sum_{n = 1}^\infty \frac{1}{16^n n} + 3 \sum_{n = 1}^\infty \frac{1}{81^n n} + 5 \sum_{n = 1}^\infty \frac{1}{25^n n} . }[/math]
- [math]\displaystyle{ \ln 2 = \frac{14}{31} \sum_{k = 0}^\infty \frac{1}{961^{k}(2k+1)} + \frac{6}{161} \sum_{k = 0}^\infty \frac{1}{25921^{k}(2k+1)} + \frac{10}{49} \sum_{k = 0}^\infty \frac{1}{2401^{k}(2k+1)} . }[/math]
Representation as integrals
The natural logarithm of 2 occurs frequently as the result of integration. Some explicit formulas for it include:
- [math]\displaystyle{ \int_0^1 \frac{dx}{1+x} = \int_1^2 \frac{dx}{x} = \ln 2 }[/math]
- [math]\displaystyle{ \int_0^\infty e^{-x}\frac{1-e^{-x}}{x} \, dx= \ln 2 }[/math]
- [math]\displaystyle{ \int_0^\infty 2^{-x} dx= \frac{1}{\ln 2} }[/math]
- [math]\displaystyle{ \int_0^\frac{\pi}{3} \tan x \, dx=2\int_0^\frac{\pi}{4} \tan x \, dx = \ln 2 }[/math]
- [math]\displaystyle{ -\frac{1}{\pi i}\int_{0}^{\infty} \frac{\ln x \ln\ln x}{(x+1)^2} \, dx= \ln 2 }[/math]
Other representations
The Pierce expansion is OEIS: A091846
- [math]\displaystyle{ \ln 2 = 1 -\frac{1}{1\cdot 3}+\frac{1}{1\cdot 3\cdot 12} -\cdots. }[/math]
The Engel expansion is OEIS: A059180
- [math]\displaystyle{ \ln 2 = \frac{1}{2} + \frac{1}{2\cdot 3} + \frac{1}{2\cdot 3\cdot 7} + \frac{1}{2\cdot 3\cdot 7\cdot 9}+\cdots. }[/math]
The cotangent expansion is OEIS: A081785
- [math]\displaystyle{ \ln 2 = \cot({\arccot(0) -\arccot(1) + \arccot(5) - \arccot(55) + \arccot(14187) -\cdots}). }[/math]
The simple continued fraction expansion is OEIS: A016730
- [math]\displaystyle{ \ln 2 = \left[ 0; 1, 2, 3, 1, 6, 3, 1, 1, 2, 1, 1, 1, 1, 3, 10, 1, 1, 1, 2, 1, 1, 1, 1, 3, 2, 3, 1,...\right] }[/math],
which yields rational approximations, the first few of which are 0, 1, 2/3, 7/10, 9/13 and 61/88.
This generalized continued fraction:
- [math]\displaystyle{ \ln 2 = \left[ 0;1,2,3,1,5,\tfrac{2}{3},7,\tfrac{1}{2},9,\tfrac{2}{5},...,2k-1,\frac{2}{k},...\right] }[/math],[1]
- also expressible as
- [math]\displaystyle{ \ln 2 = \cfrac{1} {1+\cfrac{1} {2+\cfrac{1} {3+\cfrac{2} {2+\cfrac{2} {5+\cfrac{3} {2+\cfrac{3} {7+\cfrac{4} {2+\ddots}}}}}}}} = \cfrac{2} {3-\cfrac{1^2} {9-\cfrac{2^2} {15-\cfrac{3^2} {21-\ddots}}}} }[/math]
Bootstrapping other logarithms
Given a value of ln 2, a scheme of computing the logarithms of other integers is to tabulate the logarithms of the prime numbers and in the next layer the logarithms of the composite numbers c based on their factorizations
- [math]\displaystyle{ c=2^i3^j5^k7^l\cdots\rightarrow \ln(c)=i\ln(2)+j\ln(3)+k\ln(5)+l\ln(7)+\cdots }[/math]
This employs
| prime | approximate natural logarithm | OEIS |
|---|---|---|
| 2 | 0.693147180559945309417232121458 | A002162 |
| 3 | 1.09861228866810969139524523692 | A002391 |
| 5 | 1.60943791243410037460075933323 | A016628 |
| 7 | 1.94591014905531330510535274344 | A016630 |
| 11 | 2.39789527279837054406194357797 | A016634 |
| 13 | 2.56494935746153673605348744157 | A016636 |
| 17 | 2.83321334405621608024953461787 | A016640 |
| 19 | 2.94443897916644046000902743189 | A016642 |
| 23 | 3.13549421592914969080675283181 | A016646 |
| 29 | 3.36729582998647402718327203236 | A016652 |
| 31 | 3.43398720448514624592916432454 | A016654 |
| 37 | 3.61091791264422444436809567103 | A016660 |
| 41 | 3.71357206670430780386676337304 | A016664 |
| 43 | 3.76120011569356242347284251335 | A016666 |
| 47 | 3.85014760171005858682095066977 | A016670 |
| 53 | 3.97029191355212183414446913903 | A016676 |
| 59 | 4.07753744390571945061605037372 | A016682 |
| 61 | 4.11087386417331124875138910343 | A016684 |
| 67 | 4.20469261939096605967007199636 | A016690 |
| 71 | 4.26267987704131542132945453251 | A016694 |
| 73 | 4.29045944114839112909210885744 | A016696 |
| 79 | 4.36944785246702149417294554148 | A016702 |
| 83 | 4.41884060779659792347547222329 | A016706 |
| 89 | 4.48863636973213983831781554067 | A016712 |
| 97 | 4.57471097850338282211672162170 | A016720 |
In a third layer, the logarithms of rational numbers r = a/b are computed with ln(r) = ln(a) − ln(b), and logarithms of roots via ln n√c = 1/n ln(c).
The logarithm of 2 is useful in the sense that the powers of 2 are rather densely distributed; finding powers 2i close to powers bj of other numbers b is comparatively easy, and series representations of ln(b) are found by coupling 2 to b with logarithmic conversions.
Example
If ps = qt + d with some small d, then ps/qt = 1 + d/qt and therefore
- [math]\displaystyle{ s\ln p -t\ln q = \ln\left(1+\frac{d}{q^t}\right) = \sum_{m=1}^\infty (-1)^{m+1}\frac{(\frac{d}{q^t})^m}{m} = \sum_{n=0}^\infty \frac{2}{2n+1} {\left(\frac{d}{2 q^t + d}\right)}^{2n+1} . }[/math]
Selecting q = 2 represents ln p by ln 2 and a series of a parameter d/qt that one wishes to keep small for quick convergence. Taking 32 = 23 + 1, for example, generates
- [math]\displaystyle{ 2\ln 3 = 3\ln 2 -\sum_{k\ge 1}\frac{(-1)^k}{8^{k}k} = 3\ln 2 + \sum_{n=0}^\infty \frac{2}{2n+1} {\left(\frac{1}{2 \cdot 8 + 1}\right)}^{2n+1} . }[/math]
This is actually the third line in the following table of expansions of this type:
| s | p | t | q | d/qt |
|---|---|---|---|---|
| 1 | 3 | 1 | 2 | 1/2 = 0.50000000… |
| 1 | 3 | 2 | 2 | −1/4 = −0.25000000… |
| 2 | 3 | 3 | 2 | 1/8 = 0.12500000… |
| 5 | 3 | 8 | 2 | −13/256 = −0.05078125… |
| 12 | 3 | 19 | 2 | 7153/524288 = 0.01364326… |
| 1 | 5 | 2 | 2 | 1/4 = 0.25000000… |
| 3 | 5 | 7 | 2 | −3/128 = −0.02343750… |
| 1 | 7 | 2 | 2 | 3/4 = 0.75000000… |
| 1 | 7 | 3 | 2 | −1/8 = −0.12500000… |
| 5 | 7 | 14 | 2 | 423/16384 = 0.02581787… |
| 1 | 11 | 3 | 2 | 3/8 = 0.37500000… |
| 2 | 11 | 7 | 2 | −7/128 = −0.05468750… |
| 11 | 11 | 38 | 2 | 10433763667/274877906944 = 0.03795781… |
| 1 | 13 | 3 | 2 | 5/8 = 0.62500000… |
| 1 | 13 | 4 | 2 | −3/16 = −0.18750000… |
| 3 | 13 | 11 | 2 | 149/2048 = 0.07275391… |
| 7 | 13 | 26 | 2 | −4360347/67108864 = −0.06497423… |
| 10 | 13 | 37 | 2 | 419538377/137438953472 = 0.00305254… |
| 1 | 17 | 4 | 2 | 1/16 = 0.06250000… |
| 1 | 19 | 4 | 2 | 3/16 = 0.18750000… |
| 4 | 19 | 17 | 2 | −751/131072 = −0.00572968… |
| 1 | 23 | 4 | 2 | 7/16 = 0.43750000… |
| 1 | 23 | 5 | 2 | −9/32 = −0.28125000… |
| 2 | 23 | 9 | 2 | 17/512 = 0.03320312… |
| 1 | 29 | 4 | 2 | 13/16 = 0.81250000… |
| 1 | 29 | 5 | 2 | −3/32 = −0.09375000… |
| 7 | 29 | 34 | 2 | 70007125/17179869184 = 0.00407495… |
| 1 | 31 | 5 | 2 | −1/32 = −0.03125000… |
| 1 | 37 | 5 | 2 | 5/32 = 0.15625000… |
| 4 | 37 | 21 | 2 | −222991/2097152 = −0.10633039… |
| 5 | 37 | 26 | 2 | 2235093/67108864 = 0.03330548… |
| 1 | 41 | 5 | 2 | 9/32 = 0.28125000… |
| 2 | 41 | 11 | 2 | −367/2048 = −0.17919922… |
| 3 | 41 | 16 | 2 | 3385/65536 = 0.05165100… |
| 1 | 43 | 5 | 2 | 11/32 = 0.34375000… |
| 2 | 43 | 11 | 2 | −199/2048 = −0.09716797… |
| 5 | 43 | 27 | 2 | 12790715/134217728 = 0.09529825… |
| 7 | 43 | 38 | 2 | −3059295837/274877906944 = −0.01112965… |
Starting from the natural logarithm of q = 10 one might use these parameters:
| s | p | t | q | d/qt |
|---|---|---|---|---|
| 10 | 2 | 3 | 10 | 3/125 = 0.02400000… |
| 21 | 3 | 10 | 10 | 460353203/10000000000 = 0.04603532… |
| 3 | 5 | 2 | 10 | 1/4 = 0.25000000… |
| 10 | 5 | 7 | 10 | −3/128 = −0.02343750… |
| 6 | 7 | 5 | 10 | 17649/100000 = 0.17649000… |
| 13 | 7 | 11 | 10 | −3110989593/100000000000 = −0.03110990… |
| 1 | 11 | 1 | 10 | 1/10 = 0.10000000… |
| 1 | 13 | 1 | 10 | 3/10 = 0.30000000… |
| 8 | 13 | 9 | 10 | −184269279/1000000000 = −0.18426928… |
| 9 | 13 | 10 | 10 | 604499373/10000000000 = 0.06044994… |
| 1 | 17 | 1 | 10 | 7/10 = 0.70000000… |
| 4 | 17 | 5 | 10 | −16479/100000 = −0.16479000… |
| 9 | 17 | 11 | 10 | 18587876497/100000000000 = 0.18587876… |
| 3 | 19 | 4 | 10 | −3141/10000 = −0.31410000… |
| 4 | 19 | 5 | 10 | 30321/100000 = 0.30321000… |
| 7 | 19 | 9 | 10 | −106128261/1000000000 = −0.10612826… |
| 2 | 23 | 3 | 10 | −471/1000 = −0.47100000… |
| 3 | 23 | 4 | 10 | 2167/10000 = 0.21670000… |
| 2 | 29 | 3 | 10 | −159/1000 = −0.15900000… |
| 2 | 31 | 3 | 10 | −39/1000 = −0.03900000… |
Known digits
This is a table of recent records in calculating digits of ln 2. As of December 2018, it has been calculated to more digits than any other natural logarithm[2][3] of a natural number, except that of 1.
| Date | Name | Number of digits |
|---|---|---|
| January 7, 2009 | A.Yee & R.Chan | 15,500,000,000 |
| February 4, 2009 | A.Yee & R.Chan | 31,026,000,000 |
| February 21, 2011 | Alexander Yee | 50,000,000,050 |
| May 14, 2011 | Shigeru Kondo | 100,000,000,000 |
| February 28, 2014 | Shigeru Kondo | 200,000,000,050 |
| July 12, 2015 | Ron Watkins | 250,000,000,000 |
| January 30, 2016 | Ron Watkins | 350,000,000,000 |
| April 18, 2016 | Ron Watkins | 500,000,000,000 |
| December 10, 2018 | Michael Kwok | 600,000,000,000 |
| April 26, 2019 | Jacob Riffee | 1,000,000,000,000 |
| August 19, 2020 | Seungmin Kim[4][5] | 1,200,000,000,100 |
| September 9, 2021 | William Echols[6][7] | 1,500,000,000,000 |
See also
- Rule of 72, in which ln 2 figures prominently
- Half-life, in which ln 2 figures prominently
- Erdős–Moser equation: all solutions must come from a convergent of ln 2.
References
- Brent, Richard P. (1976). "Fast multiple-precision evaluation of elementary functions". J. ACM 23 (2): 242–251. doi:10.1145/321941.321944.
- Uhler, Horace S. (1940). "Recalculation and extension of the modulus and of the logarithms of 2, 3, 5, 7 and 17". Proc. Natl. Acad. Sci. U.S.A. 26 (3): 205–212. doi:10.1073/pnas.26.3.205. PMID 16588339. Bibcode: 1940PNAS...26..205U.
- Sweeney, Dura W. (1963). "On the computation of Euler's constant". Mathematics of Computation 17 (82): 170–178. doi:10.1090/S0025-5718-1963-0160308-X.
- Chamberland, Marc (2003). "Binary BBP-formulae for logarithms and generalized Gaussian–Mersenne primes". Journal of Integer Sequences 6: 03.3.7. Bibcode: 2003JIntS...6...37C. http://www.emis.de/journals/JIS/VOL6/Chamberland/chamberland60.pdf. Retrieved 2010-04-29.
- Gourévitch, Boris; Guillera Goyanes, Jesús (2007). "Construction of binomial sums for π and polylogarithmic constants inspired by BBP formulas". Applied Math. E-Notes 7: 237–246. http://www.math.nthu.edu.tw/~amen/2007/061028-2.pdf.
- Wu, Qiang (2003). "On the linear independence measure of logarithms of rational numbers". Mathematics of Computation 72 (242): 901–911. doi:10.1090/S0025-5718-02-01442-4.
- ↑ Borwein, J.; Crandall, R.; Free, G. (2004). "On the Ramanujan AGM Fraction , I: The Real-Parameter Case". Exper. Math. 13 (3): 278–280. doi:10.1080/10586458.2004.10504540. http://www.kurims.kyoto-u.ac.jp/EMIS/journals/EM/expmath/volumes/13/13.3/BorweinCrandallFee.pdf.
- ↑ "y-cruncher". numberworld.org. http://www.numberworld.org/y-cruncher/. Retrieved 10 December 2018.
- ↑ "Natural log of 2". numberworld.org. http://www.numberworld.org/digits/Log(2)/. Retrieved 10 December 2018.
- ↑ "Records set by y-cruncher". http://www.numberworld.org/y-cruncher/.
- ↑ "Natural logarithm of 2 (Log(2)) world record by Seungmin Kim". 19 August 2020. https://ehfd.github.io/world-record/natural-logarithm-of-2-log2/.
- ↑ "Records set by y-cruncher". http://www.numberworld.org/y-cruncher/records.html.
- ↑ "Natural Log of 2 - William Echols". https://williamechols.com/ln2/.
External links
- Weisstein, Eric W.. "Natural logarithm of 2". http://mathworld.wolfram.com/NaturalLogarithmof2.html.
- Gourdon, Xavier; Sebah, Pascal. "The logarithm constant:log 2". http://numbers.computation.free.fr/Constants/Log2/log2.html.
|  | |
 |  |
