19 (number)

From HandWiki
Short description: Natural number
← 18 19 20 →
Cardinalnineteen
Ordinal19th
(nineteenth)
Numeral systemnonadecimal
Factorizationprime
Prime8th
Divisors1, 19
Greek numeralΙΘ´
Roman numeralXIX
Binary100112
Ternary2013
Quaternary1034
Quinary345
Senary316
Octal238
Duodecimal1712
Hexadecimal1316
VigesimalJ20
Base 36J36

19 (nineteen) is the natural number following 18 and preceding 20. It is a prime number.

Mathematics

19 is a centered triangular number.

[math]\displaystyle{ 19 }[/math] is the eighth prime number, and forms a sexy prime with 13,[1] a twin prime with 17,[2] and a cousin prime with 23.[3] It is the third full reptend prime in decimal,[4] the fifth central trinomial coefficient,[5] and the seventh Mersenne prime exponent.[6] 19 is the second Keith number, and more specifically the first Keith prime.[7] It is also the second octahedral number, after 6.[8]

  • R19 is the second base-10 repunit prime, short for the number 1111111111111111111.[9]
  • 19 is the maximum number of fourth powers needed to sum up to any natural number, and in the context of Waring's problem, 19 is the fourth value of g(k).[10]
  • The sum of the squares of the first 19 primes is divisible by 19.[11]
  • 19 is the sixth Heegner number.[12] 67 and 163, respectively the 19th and 38th prime numbers, are the two largest Heegner numbers, of nine total.
The 19th triangular number is 190, equivalently the sum of the first 19 non-zero integers, that is also the sixth centered nonagonal number.[15][16]
19 is the first number in an infinite sequence of numbers in decimal whose digits start with 1 and have trailing 9's, that form triangular numbers containing trailing zeroes in proportion to 9s present in the original number; i.e. 19900 is the 199th triangular number, and 1999000 is the 1999th.[17]
Like 19, 199 and 1999 are also both prime, as are 199999 and 19999999. In fact, a number of the form 19n, where n is the number of nines that terminate in the number, is prime for:
n = {1, 2, 3, 5, 7, 26, 27, 53, 147, 236, 248, 386, 401}.[18]
  • 19, alongside 109, 1009, and 10009, are all prime (with 109 also full reptend), and form part of a sequence of numbers where inserting a digit inside the previous term produces the next smallest prime possible, up to scale, with the composite number 9 as root.[19] 100019 is the next such smallest prime number, by the insertion of a 1.
Numbers of the form 10n9 equivalent to 10x + 9 with x = n + 1, where n is the number of zeros in the term, are prime for n = {0, 1, 2, 3, 8, 17, 21, 44, 48, 55, 68, 145, 201, 271, 2731, 4563}, and probably prime for n = {31811, 43187, 48109, 92691}.[20]
  • The Collatz sequence for nine requires nineteen steps to return back to one, more than any other number below it.[21] On the other hand, nineteen requires twenty steps, like eighteen. Less than ten thousand, only thirty-one other numbers require nineteen steps to return back to one:
{56, 58, 60, 61, 352, 360, 362, 368, 369, 372, 373, 401, 402, 403, 2176, ..., and 2421}.[22]
  • 19 is the first prime number that is not a permutable prime in decimal, as its reverse (91) is composite; where 91 is also the fourth centered nonagonal number.[16]
19 × 91 = 1729, the first Hardy-Ramanujan number or taxicab number, also a Harshad number in base-ten, as it's divisible by the sum of its digits, 19.[23][24]
1729 is also the nineteenth dodecagonal number.[25]
Distinguishably, the only nontrivial normal magic hexagon is composed of nineteen cells, where every diagonal of consecutive hexagons has sums equal to 38, or twice 19.[27]
A hexaflexagon is a strip of nineteen alternating triangular faces that can flex into a regular hexagon, such that any two of six colorings on triangles can be oriented to align on opposite sides of the folded figure.Cite error: Closing </ref> missing for <ref> tag
  • [math]\displaystyle{ \tfrac {1} {19} }[/math] can be used to generate the first full, non-normal prime reciprocal magic square in decimal whose rows, columns and diagonals — in a 18 x 18 array — all generate a magic constant of 81 = 92.[28]
The next prime number to generate a like-magic square in base-ten is 383,[29] the seventy-sixth prime number (where 19 × 4 = 76).[30] A regular 19 x 19 magic square, on the other hand, has a magic constant [math]\displaystyle{ M_{19} }[/math] of 3439 = 19 × 181.[31]
  • The projective special linear group [math]\displaystyle{ \mathrm {L(19)} }[/math] represents the abstract structure of the 57-cell: a universal 4-polytope with a total of one hundred and seventy-one (171 = 9 × 19) edges and vertices, and fifty-seven (57 = 3 × 19) hemi-icosahedral cells that are self-dual.[32]
In total, there are nineteen Coxeter groups of non-prismatic uniform honeycombs in the fourth dimension: five Coxeter honeycomb groups exist in Euclidean space, while the other fourteen Coxeter groups are compact and paracompact hyperbolic honeycomb groups. There are also specifically nineteen uniform honeycombs inside the Euclidean [math]\displaystyle{ {\tilde{C}}_4 }[/math] tesseractic honeycomb group in 4-space. In 5-space, there are nineteen uniform polytopes with [math]\displaystyle{ \mathrm A_{5} }[/math] simplex symmetry.
  • There are infinitely many finite-volume Vinberg polytopes up through dimension nineteen, which generate hyperbolic tilings with degenerate simplex quadrilateral pyramidal domains, as well as prismatic domains and otherwise.[33]
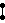
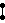
Vinberg polytopes of lowest rank n + 2 mirrors exist up through the seventeenth dimension, where there exists a unique figure with nineteen facets.[34] It is expressed with the simple Dynkin diagram, CDel nodea.pngCDel 3a.pngCDel nodea.pngCDel 3a.pngCDel branch.pngCDel 3a.pngCDel nodea.pngCDel 3a.pngCDel nodea.pngCDel 3a.pngCDel nodea.pngCDel 3a.pngCDel nodea.pngCDel 3a.pngCDel nodea.pngCDel 3a.pngCDel nodea.pngCDel 3a.pngCDel nodea.pngCDel 3a.pngCDel nodea.pngCDel 3a.pngCDel nodea.pngCDel 3a.pngCDel nodea.pngCDel 3a.pngCDel nodea.pngCDel 3a.pngCDel branch.pngCDel 3a.pngCDel nodea.pngCDel 3a.pngCDel nodea.png.
On the other hand, a cubic surface is the zero set in [math]\displaystyle{ \mathbb {P^{3}} }[/math] of a homogeneous cubic polynomial in four variables [math]\displaystyle{ f = c_3000x^3_1 + c_2100x^2_1x_2 + c_1200x^1x^2_2 + c_0300x^3_2 + \cdots + c_0003x^3_4, }[/math] a polynomial with a total of twenty coefficients, which specifies a space for cubic surfaces that is 19-dimensional.[35]
  • 19 is the eighth consecutive supersingular prime. It is the middle indexed member in the sequence of fifteen such primes that divide the order of the Friendly Giant [math]\displaystyle{ \mathrm {F_{1}} }[/math], the largest sporadic group: {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 47, 59, 71}.[36]
Janko groups [math]\displaystyle{ \mathrm {J_{1}} }[/math] and [math]\displaystyle{ \mathrm {J_{3}} }[/math] are the two-smallest of six pariah groups that are not subquotients of [math]\displaystyle{ \mathrm {F_{1}} }[/math], which contain 19 as the largest prime number that divides their orders.[37]
[math]\displaystyle{ \mathrm {J_{1}} }[/math] holds (2,3,7) as standard generators (a,b,ab) that yield a semi-presentation where o(abab2) = 19, while [math]\displaystyle{ \mathrm {J_{3}} }[/math] holds as standard generators (2A, 3A, 19), where o([a, b]) = 9.[38][39]
The Tits group [math]\displaystyle{ \mathrm {T} }[/math], as the only non-strict group of Lie type that can loosely categorize as sporadic, has group order 211 · 33 · 52 · 13, whose prime factors (inclusive of powers) generate a sum equal to 54, which is the smallest non-trivial 19-gonal number.[40]

In the Happy Family of sporadic groups, nineteen of twenty-six such groups are subquotients of the Friendly Giant, which is also its own subquotient.[41] If the Tits group is indeed included as a group of Lie type,[42] then there are nineteen classes of finite simple groups that are not sporadic groups.

Worth noting, 26 is the only number to lie between a perfect square (52) and a cube (33); if all primes in the prime factorizations of 25 and 27 are added together, a sum of 19 is obtained.

Science

The James Webb Space Telescope features a design of 19 hexagons.
  • 19 is the atomic number of potassium.
  • 19 years is very close to 235 lunations. See Metonic cycle.
  • COVID-19 is the shortened name of Coronavirus disease 2019, the cause of the global pandemic that began in 2019.
  • The James Webb Space Telescope's optical elements are in an array of 19 hexagons, wherein 18 segmented primary mirrors focus light into a centered secondary mirror situated above the collecting mirrors, that in-turn reflects back onto the telescope's central imagers. It is a shape akin to the order-3 magic hexagon.

Religion

Islam

  • The number of angels guarding Hell ("Hellfire") ("Saqar") according to the Qur'an: "Over it are nineteen" (74:30), after which the Qur'an describes this number as being "a trial for those who disbelieve" (74:31), a sign for people of the scripture to be "convinced" (74:31) and that believers "will increase in faith" (74:31) due to it.
  • The Number of Verse and Sura together in the Qur'an which announces Jesus son of Maryam's (Mary's) birth (Qur'an 19:19).
  • A group called United Submitter International claim the Quran has mathematical structure based on the number 19. The gematrical value of WAHD = 6+1+8+4=19, Wahd means 'One' (God) to the first verse (1:1), known as Bas-malah, consists of 19 Arabic letters or the Quran consists of 114 (19x6) surat etc.

Baháʼí faith

In the Bábí and Baháʼí Faiths, a group of 19 is called a Váhid, a Unity (Arabic: واحد). The numerical value of this word in the Abjad numeral system is 19.

  • The Baháʼí calendar is structured such that a year contains 19 months of 19 days each (along with the intercalary period of Ayyám-i-Há), as well as a 19-year cycle and a 361-year (19x19) supercycle.
  • The Báb and his disciples formed a group of 19.
  • There were 19 Apostles of Bahá'u'lláh.

Celtic paganism

19 is a sacred number of the goddess Brigid because it is said to represent the 19-year cycle of the Great Celtic Year and the amount of time it takes the Moon to coincide with the winter solstice.[43]

Music

  • "19" is a 1985 song by Paul Hardcastle, including sampled soundbites taken from a documentary about the Vietnam War in which 19 is claimed to have been the average age of United States soldiers killed in the conflict.[44] The song was parodied by British satirist Rory Bremner under the pseudonym 'The Commentators,' as N-n-nineteen, Not Out, the title referring to the batting average of David Gower, the England cricket captain, during his side's risible performance against the West Indies in 1984 when they lost 5–0.
  • "I Was Only Nineteen" by the Australian group Redgum reached number one on the Australian charts in 1983. In 2005 a hip hop version of the song was produced by The Herd.
  • 19 is the name of Adele's 2008 debut album, so named since she was 19 years old at the time.
  • "Hey Nineteen" is a song by American jazz rock band Steely Dan, on the 1980 album Gaucho.
  • Nineteen has been used as an alternative to twelve for a division of the octave into equal parts. This idea goes back to Salinas in the sixteenth century, and is interesting in part because it gives a system of meantone tuning, being close to 1/3 comma meantone. See 19 equal temperament.
  • Some organs use the 19th harmonic to approximate a minor third.

Literature

  • Stephen King's eight-book epic The Dark Tower saga employs the number 19 in books The Dark Tower: The Gunslinger, The Dark Tower V: Wolves of the Calla, The Dark Tower VI: Song of Susannah, The Dark Tower VII: The Dark Tower, and The Wind Through the Keyhole as a mysterious and important number. They refer to the "ka-tet of 19", "Directive Nineteen," many names add up to 19, 19 seems to permeate every aspect of Roland and his traveler's lives. In addition, the number ends up being a powerful key.
  • In Jodi Picoult's bestselling book Nineteen Minutes, the number 19 is referenced multiple times. It is most commonly referenced when referring to the main subject of the book, the school shooting rampage that took place over a span of 19 minutes.
  • The novel S. by Doug Dorst uses 19 and its multiples throughout. S is the 19th letter of the alphabet.

Games

A 19x19 Go board
  • The game of Go is played on a grid of 19×19 lines (though variants can be played on grids of other sizes).
  • Though the maximum score for a cribbage hand is 29, there is no combination of cards that adds up to 19 points. Many cribbage players, therefore, jokingly refer to a zero-point hand as "a 19 hand".
  • In the base version of Settlers of Catan there are 19 hexagonal pieces that can be randomly or intentionally placed to form the board.

Age 19

  • In four countries, 19 is the age of majority.
  • In two countries, 19 is the minimum legal drinking age.
  • In three countries, 19 is the minimum legal smoking age.

In sports

  • In golf, the '19th hole' is the clubhouse bar and in match play, if there is a tie after 18 holes, an extra hole(s) is played. In miniature golf it is an extra hole on which the winner earns an instant prize.

In other fields

  • The 19th Amendment to the United States Constitution gave American women the right to vote.
  • The Vietnam War spanned over 19 years, from November 1955 to April 1975.

References

  1. ↑ Sloane, N. J. A., ed. "Sequence A046117 (Primes p such that p-6 is also prime. (Upper of a pair of sexy primes.))". OEIS Foundation. https://oeis.org/A046117. Retrieved 2022-08-05. 
  2. ↑ Sloane, N. J. A., ed. "Sequence A006512 (Greater of twin primes.)". OEIS Foundation. https://oeis.org/A006512. Retrieved 2022-08-05. 
  3. ↑ Sloane, N. J. A., ed. "Sequence A088762 (Numbers n such that (2n-1, 2n+3) is a cousin prime pair.)". OEIS Foundation. https://oeis.org/A088762. Retrieved 2022-08-05. 
  4. ↑ Sloane, N. J. A., ed. "Sequence A001913 (Full reptend primes: primes with primitive root 10.)". OEIS Foundation. https://oeis.org/A001913. Retrieved 2022-08-05. 
  5. ↑ Sloane, N. J. A., ed. "Sequence A002426 (Central trinomial coefficients: largest coefficient of (1 + x + x^2)^n.)". OEIS Foundation. https://oeis.org/A002426. Retrieved 2022-08-05. 
  6. ↑ "Sloane's A000043 : Mersenne exponents". OEIS Foundation. https://oeis.org/A000043. 
  7. ↑ Sloane, N. J. A., ed. "Sequence A007629 (Repfigit (REPetitive FIbonacci-like diGIT) numbers (or Keith numbers).)". OEIS Foundation. https://oeis.org/A007629. Retrieved 2022-08-05. 
  8. ↑ Sloane, N. J. A., ed. "Sequence A005900 (Octahedral numbers)". OEIS Foundation. https://oeis.org/A005900. Retrieved 2016-08-17. 
  9. ↑ Guy, Richard; Unsolved Problems in Number Theory, p. 7 ISBN:1475717385
  10. ↑ Sloane, N. J. A., ed. "Sequence A002804 ((Presumed) solution to Waring's problem.)". OEIS Foundation. https://oeis.org/A002804. Retrieved 2022-08-05. 
  11. ↑ Sloane, N. J. A., ed. "Sequence A111441 (Numbers k such that the sum of the squares of the first k primes is divisible by k)". OEIS Foundation. https://oeis.org/A111441. Retrieved 2022-06-02. 
  12. ↑ "Sloane's A003173 : Heegner numbers". OEIS Foundation. https://oeis.org/A003173. 
  13. ↑ "Sloane's A125602 : Centered triangular numbers that are prime". OEIS Foundation. https://oeis.org/A125602. 
  14. ↑ "Sloane's A003215 : Hex (or centered hexagonal) numbers". OEIS Foundation. https://oeis.org/A003215. 
  15. ↑ Sloane, N. J. A., ed. "Sequence A000217 (Triangular numbers)". OEIS Foundation. https://oeis.org/A000217. Retrieved 2022-07-13. 
  16. ↑ 16.0 16.1 Sloane, N. J. A., ed. "Sequence A060544 (Centered 9-gonal (also known as nonagonal or enneagonal) numbers. Every third triangular number, starting with 1)". OEIS Foundation. https://oeis.org/A060544. Retrieved 2022-11-30. 
  17. ↑ Sloane, N. J. A.. "Sequence A186076". https://oeis.org/A186076. ""Note that terms A186074(4) and A186074(10) have trailing 0's, i.e. 19900 = Sum_{k=0..199} k and 1999000 = Sum_{k=0..1999} k...". "This pattern continues indefinitely: 199990000, 19999900000, etc."" 
  18. ↑ Sloane, N. J. A., ed. "Sequence A055558 (Primes of the form 1999...999)". OEIS Foundation. https://oeis.org/A055558. Retrieved 2022-07-26. 
  19. ↑ Sloane, N. J. A., ed. "Sequence A068174 (Define an increasing sequence as follows. Start with an initial term, the seed (which need not have the property of the sequence); subsequent terms are obtained by inserting/placing at least one digit in the previous term to obtain the smallest number with the given property. Here the property is be a prime.)". OEIS Foundation. https://oeis.org/A068174. Retrieved 2022-07-26. 
  20. ↑ Sloane, N. J. A., ed. "Sequence A088275 (Numbers n such that 10^n + 9 is prime)". OEIS Foundation. https://oeis.org/A088275. Retrieved 2022-07-28. 
  21. ↑ Sloane, N. J. A.. "3x+1 problem". OEIS Foundation. http://oeis.org/wiki/3x%2B1_problem. 
  22. ↑ Sloane, N. J. A., ed. "Sequence A006577 (Number of halving and tripling steps to reach 1 in '3x+1' problem, or -1 if 1 is never reached)". OEIS Foundation. https://oeis.org/A006577. Retrieved 2023-01-24. 
    "Table of n, a(n) for n = 1..10000".
  23. ↑ "19". https://primes.utm.edu/curios/page.php/19.html. 
  24. ↑ Sloane, N. J. A., ed. "Sequence A005349 (Niven (or Harshad, or harshad) numbers: numbers that are divisible by the sum of their digits.)". OEIS Foundation. https://oeis.org/A005349. Retrieved 2022-10-11. 
  25. ↑ Sloane, N. J. A., ed. "Sequence A051624 (12-gonal (or dodecagonal) numbers: a(n) equal to n*(5*n-4).)". OEIS Foundation. https://oeis.org/A051624. Retrieved 2023-12-21. 
  26. ↑ Sloane, N. J. A., ed. "Sequence A007569 (Number of nodes in regular n-gon with all diagonals drawn.)". OEIS Foundation. https://oeis.org/A007569. Retrieved 2023-04-04. 
  27. ↑ Trigg, C. W. (February 1964). "A Unique Magic Hexagon". Recreational Mathematics Magazine. http://www.mathematik.uni-bielefeld.de/~sillke/PUZZLES/magic-hexagon-trigg. Retrieved 2022-07-14. 
  28. ↑ Andrews, William Symes (1917). Magic Squares and Cubes. Chicago, IL: Open Court Publishing Company. pp. 176, 177. ISBN 9780486206585. OCLC 1136401. http://djm.cc/library/Magic_Squares_Cubes_Andrews_edited.pdf. 
  29. ↑ Sloane, N. J. A., ed. "Sequence A072359 (Primes p such that the p-1 digits of the decimal expansion of k/p (for k equal to 1,2,3,...,p-1) fit into the k-th row of a magic square grid of order p-1.)". OEIS Foundation. https://oeis.org/A072359. Retrieved 2023-09-04. 
  30. ↑ Sloane, N. J. A., ed. "Sequence A000040 (The prime numbers)". OEIS Foundation. https://oeis.org/A000040. Retrieved 2023-09-06. 
  31. ↑ Sloane, N. J. A., ed. "Sequence A006003 (a(n) equal to n*(n^2 + 1)/2.)". OEIS Foundation. https://oeis.org/A006003. Retrieved 2023-09-04. 
  32. ↑ Coxeter, H. S. M. (1982). "Ten toroids and fifty-seven hemidodecahedra". Geometriae Dedicata 13 (1): 87–99. doi:10.1007/BF00149428. 
  33. ↑ Allcock, Daniel (11 July 2006). "Infinitely many hyperbolic Coxeter groups through dimension 19". Geometry & Topology 10 (2): 737–758. doi:10.2140/gt.2006.10.737. 
  34. ↑ Tumarkin, P. (2004). "Hyperbolic Coxeter n-polytopes with n + 2 facets". Mathematical Notes (Springer) 75 (5/6): 848–854. doi:10.1023/B:MATN.0000030993.74338.dd. 
  35. ↑ Seigal, Anna (2020). "Ranks and symmetric ranks of cubic surfaces". Journal of Symbolic Computation (Amsterdam: Elsevier) 101: 304–306. doi:10.1016/j.jsc.2019.10.001. Bibcode: 2018arXiv180105377S. https://www.sciencedirect.com/science/article/abs/pii/S074771711930104X. 
  36. ↑ Sloane, N. J. A., ed. "Sequence A002267 (The 15 supersingular primes.)". OEIS Foundation. https://oeis.org/A002267. Retrieved 2022-12-11. 
  37. ↑ Ronan, Mark (2006). Symmetry and the Monster: One of the Greatest Quests of Mathematics. New York: Oxford University Press. pp. 244–246. doi:10.1007/s00283-008-9007-9. ISBN 978-0-19-280722-9. OCLC 180766312. 
  38. ↑ Wilson, R.A (1998). "Chapter: An Atlas of Sporadic Group Representations". The Atlas of Finite Groups - Ten Years On (LMS Lecture Note Series 249). Cambridge, U.K: Cambridge University Press. p. 267. doi:10.1017/CBO9780511565830.024. ISBN 9780511565830. OCLC 726827806. https://webspace.maths.qmul.ac.uk/r.a.wilson/pubs_files/ASGRweb.pdf. 
    List of standard generators of all sporadic groups.
  39. ↑ Nickerson, S.J.; Wilson, R.A. (2011). "Semi-Presentations for the Sporadic Simple Groups". Experimental Mathematics (Oxfordshire: Taylor & Francis) 14 (3): 365. doi:10.1080/10586458.2005.10128927. https://www.tandfonline.com/doi/abs/10.1080/10586458.2005.10128927. 
  40. ↑ Sloane, N. J. A., ed. "Sequence A051871 (19-gonal (or enneadecagonal) numbers: n(17n-15)/2.)". OEIS Foundation. https://oeis.org/A051871. Retrieved 2023-12-09. 
  41. ↑ John F.R. Duncan; Michael H. Mertens; Ken Ono (2017). "Pariah moonshine". Nature Communications 8 (1): 2 (Article 670). doi:10.1038/s41467-017-00660-y. PMID 28935903. Bibcode: 2017NatCo...8..670D. "...so [sic] moonshine illuminates a physical origin for the monster, and for the 19 other sporadic groups that are involved in the monster.". 
  42. ↑ R. B. Howlett; L. J. Rylands; D. E. Taylor (2001). "Matrix generators for exceptional groups of Lie type". Journal of Symbolic Computation 31 (4): 429. doi:10.1006/jsco.2000.0431. "...for all groups of Lie type, including the twisted groups of Steinberg, Suzuki and Ree (and the Tits group).". 
  43. ↑ Brigid: Triple Goddess of the Flame (Health, Hearth, & Forge)
  44. ↑ Roush, Gary (2008-06-02). "Statistics about the Vietnam War". Vietnam Helicopter Flight Crew Network. http://www.vhfcn.org/stat.html. "Assuming KIAs accurately represented age groups serving in Vietnam, the average age of an infantryman (MOS 11B) serving in Vietnam to be 19 years old is a myth, it is actually 22. None of the enlisted grades have an average age of less than 20." 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=19_(number)&oldid=3380992"