Square root of 3
Template:Infobox non-integer number
The square root of 3 is the positive real number that, when multiplied by itself, gives the number 3. It is denoted mathematically as or . It is more precisely called the principal square root of 3 to distinguish it from the negative number with the same property. The square root of 3 is an irrational number. It is also known as Theodorus' constant, after Theodorus of Cyrene, who proved its irrationality.
As of December 2013[update], its numerical value in decimal notation had been computed to at least ten billion digits.[1] Its decimal expansion, written here to 65 decimal places, is given by OEIS: A002194:
- 1.732050807568877293527446341505872366942805253810380628055806
The fraction (1.732142857...) can be used as a good approximation. Despite having a denominator of only 56, it differs from the correct value by less than (approximately , with a relative error of ). The rounded value of 1.732 is correct to within 0.01% of the actual value.
The fraction (1.73205080756...) is accurate to .
Archimedes reported a range for its value: .[2]
The lower limit is an accurate approximation for to (six decimal places, relative error ) and the upper limit to (four decimal places, relative error ).
Expressions
It can be expressed as the continued fraction [1; 1, 2, 1, 2, 1, 2, 1, …] (sequence A040001 in the OEIS).
So it is true to say:
then when :
It can also be expressed by generalized continued fractions such as
which is [1; 1, 2, 1, 2, 1, 2, 1, …] evaluated at every second term.
Geometry and trigonometry


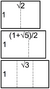
The square root of 3 can be found as the leg length of an equilateral triangle that encompasses a circle with a diameter of 1.
If an equilateral triangle with sides of length 1 is cut into two equal halves, by bisecting an internal angle across to make a right angle with one side, the right angle triangle's hypotenuse is length one, and the sides are of length and . From this, , , and .
The square root of 3 also appears in algebraic expressions for various other trigonometric constants, including[3] the sines of 3°, 12°, 15°, 21°, 24°, 33°, 39°, 48°, 51°, 57°, 66°, 69°, 75°, 78°, 84°, and 87°.
It is the distance between parallel sides of a regular hexagon with sides of length 1.
It is the length of the space diagonal of a unit cube.
The vesica piscis has a major axis to minor axis ratio equal to . This can be shown by constructing two equilateral triangles within it.
Other uses and occurrence
Power engineering
In power engineering, the voltage between two phases in a three-phase system equals times the line to neutral voltage. This is because any two phases are 120° apart, and two points on a circle 120 degrees apart are separated by times the radius (see geometry examples above).
Special functions
It is known that most roots of the nth derivatives of (where n < 18 and is the Bessel function of the first kind of order ) are transcendental. The only exceptions are the numbers , which are the algebraic roots of both and . [4][clarification needed]
See also
Other references
References
- ↑ Komsta, Łukasz (December 2013). "Computations | Łukasz Komsta". WordPress. http://www.komsta.net/computations.
- ↑ Knorr, Wilbur R. (June 1976). "Archimedes and the measurement of the circle: a new interpretation". Archive for History of Exact Sciences 15 (2): 115–140. doi:10.1007/bf00348496. https://link.springer.com/article/10.1007/BF00348496. Retrieved November 15, 2022.
- ↑ Wiseman, Julian D. A. (June 2008). "Sin and Cos in Surds". http://www.jdawiseman.com/papers/easymath/surds_sin_cos.html.
- ↑ Lorch, Lee; Muldoon, Martin E. (1995). "Transcendentality of zeros of higher dereivatives of functions involving Bessel functions". International Journal of Mathematics and Mathematical Sciences 18 (3): 551–560. doi:10.1155/S0161171295000706.
- ↑ S., D.; Jones, M. F. (1968). "22900D approximations to the square roots of the primes less than 100". Mathematics of Computation 22 (101): 234–235. doi:10.2307/2004806.
- ↑ Uhler, H. S. (1951). "Approximations exceeding 1300 decimals for , , and distribution of digits in them". Proc. Natl. Acad. Sci. U.S.A. 37 (7): 443–447. doi:10.1073/pnas.37.7.443. PMID 16578382.
- ↑ Wells, D. (1997). The Penguin Dictionary of Curious and Interesting Numbers (Revised ed.). London: Penguin Group. p. 23.
- Podestá, Ricardo A. (2020). "A geometric proof that sqrt 3, sqrt 5, and sqrt 7 are irrational". arXiv:2003.06627 [math.GM].
External links