Neural tangent kernel

Short description: Type of kernel induced by artificial neural networks

In the study of artificial neural networks (ANNs), the neural tangent kernel (NTK) is a kernel that describes the evolution of deep artificial neural networks during their training by gradient descent. It allows ANNs to be studied using theoretical tools from kernel methods.

In general, a kernel is a positive-semidefinite symmetric function of two inputs which represents some notion of similarity between the two inputs. The NTK is a specific kernel derived from a given neural network; in general, when the neural network parameters change during training, the NTK evolves as well. However, in the limit of large layer width the NTK becomes constant, revealing a duality between training the wide neural network and kernel methods: gradient descent in the infinite-width limit is fully equivalent to kernel gradient descent with the NTK. As a result, using gradient descent to minimize least-square loss for neural networks yields the same mean estimator as ridgeless kernel regression with the NTK. This duality enables simple closed form equations describing the training dynamics, generalization, and predictions of wide neural networks.

The NTK was introduced in 2018 by Arthur Jacot, Franck Gabriel and Clément Hongler, who used it to study the convergence and generalization properties of fully connected neural networks. Later works extended the NTK results to other neural network architectures. In fact, the phenomenon behind NTK is not specific to neural networks and can be observed in generic nonlinear models, usually by a suitable scaling.

Main results (informal)

Let [math]\displaystyle{ f(x;\theta ) }[/math] denote the scalar function computed by a given neural network with parameters [math]\displaystyle{ \theta }[/math] on input [math]\displaystyle{ x }[/math]. Then the neural tangent kernel is defined as[math]\displaystyle{ \Theta (x,x';\theta )=\nabla _{\theta }f(x;\theta )\cdot \nabla _{\theta }f(x';\theta ). }[/math]Since it is written as a dot product between mapped inputs (with the gradient of the neural network function serving as the feature map), we are guaranteed that the NTK is symmetric and positive semi-definite. The NTK is thus a valid kernel function.

Consider a fully connected neural network whose parameters are chosen i.i.d. according to any mean-zero distribution. This random initialization of [math]\displaystyle{ \theta }[/math] induces a distribution over [math]\displaystyle{ f(x;\theta ) }[/math] whose statistics we will analyze, both at initialization and throughout training (gradient descent on a specified dataset). We can visualize this distribution via a neural network ensemble which is constructed by drawing many times from the initial distribution over [math]\displaystyle{ f(x;\theta ) }[/math] and training each draw according to the same training procedure.

At initialization, an ensemble of wide neural networks is a zero-mean Gaussian process; during training (gradient descent on mean-square error), the ensemble evolves according to the neural tangent kernel. The converged ensemble is a Gaussian process whose mean is the ridgeless kernel regression estimator and whose variance vanishes on the training points. Here, the neural network is a scalar function trained on inputs drawn from the unit circle.

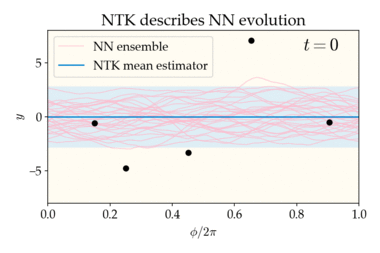
The number of neurons in each layer is called the layer’s width. Consider taking the width of every hidden layer to infinity and training the neural network with gradient descent (with a suitably small learning rate). In this infinite-width limit, several nice properties emerge:

• At initialization (before training), the neural network ensemble is a zero-mean Gaussian process (GP). This means that distribution of functions is the maximum-entropy distribution with mean [math]\displaystyle{ \mathbb {E} _{\theta }[f(x;\theta )]=0 }[/math] and covariance [math]\displaystyle{ \mathbb {E} _{\theta }[f(x;\theta )f(x';\theta )]=\Sigma (x,x') }[/math], where the GP covariance [math]\displaystyle{ \Sigma (x,x') }[/math] can be computed from the network architecture. In other words, the distribution of neural network functions at initialization has no structure other than its first and second moments (mean and covariance). This follows from the central limit theorem.
• The NTK is deterministic. In other words, the NTK is independent of the random parameter initialization.
• The NTK does not change during training.
• Each parameter changes negligibly throughout training. As Lee et al. note, "although individual parameters move by a vanishingly small amount, they collectively conspire to provide a finite change in the final output of the network, as is necessary for training."
• During training, the neural network is linearized, i.e., its parameter dependence can be captured by its first-order Taylor expansion: [math]\displaystyle{ f(x;\theta_0 +\Delta \theta )=f(x;\theta_0 )+\Delta \theta \cdot \nabla _{\theta }f(x;\theta_0 ) }[/math], where [math]\displaystyle{ \theta_0 }[/math] are the initial parameters. This follows from the fact that each parameter changes negligibly during training. (The neural network remains nonlinear with respect to the inputs.)
• The training dynamics are equivalent to kernel gradient descent using the NTK as the kernel. If the loss function is mean-squared error, the final distribution over [math]\displaystyle{ f(x;\theta ) }[/math] is still a Gaussian process, but with a new mean and covariance. In particular, the mean converges to the same estimator yielded by kernel regression with the NTK as kernel and zero ridge regularization, and the covariance is expressible in terms of the NTK and the initial GP covariance. It can be shown that the ensemble variance vanishes at the training points (in other words, the neural network always interpolates the training data, regardless of initialization).

Applications

Ridgeless kernel regression and kernel gradient descent

Kernel methods are machine learning algorithms which use only pairwise relations between input points. Kernel methods do not depend on the concrete values of the inputs; they only depend on the relations between the inputs and other inputs (such as the training set). These pairwise relations are fully captured by the kernel function: a symmetric, positive-semidefinite function of two inputs which represents some notion of similarity between the two inputs. A fully equivalent condition is that there exists some feature map [math]\displaystyle{ {\mathbf {x}}\mapsto \psi ({\mathbf {x}}) }[/math] such that the kernel function can be written as a dot product of the mapped inputs[math]\displaystyle{ K({\mathbf {x}},{\mathbf {x}}')=\psi ({\mathbf {x}})\cdot \psi ({\mathbf {x}}'). }[/math]The properties of a kernel method depend on the choice of kernel function. (Note that [math]\displaystyle{ \psi ({\mathbf {x}}) }[/math] may have higher dimension than [math]\displaystyle{ \mathbf{x} }[/math].) As a relevant example, consider linear regression. This is the task of estimating [math]\displaystyle{ {\mathbf {w}}^{*} }[/math] given [math]\displaystyle{ N }[/math] samples [math]\displaystyle{ ({\mathbf {x}}_{i},y_{i}) }[/math] generated from [math]\displaystyle{ y^{*}({\mathbf {x}})={\mathbf {w}}^{*}\cdot {\mathbf {x}} }[/math], where each [math]\displaystyle{ \mathbf {x}_{i} }[/math] is drawn according to some input data distribution. In this setup, [math]\displaystyle{ {\mathbf {w}}^{*} }[/math] is the weight vector which defines the true function [math]\displaystyle{ y^{*} }[/math]; we wish to use the training samples to develop a model [math]\displaystyle{ \mathbf {\hat {w}} }[/math] which approximates [math]\displaystyle{ {\mathbf {w}}^{*} }[/math]. We do this by minimizing the mean-square error between our model and the training samples:[math]\displaystyle{ {\mathbf {\hat {w}}}=\arg \min _{\mathbf {w}}{\frac {1}{N}}\sum_{i=0}^{N}||y^{*}({\mathbf {x}}_{i})-{\mathbf {w}}\cdot {\mathbf {x}}_{i}||^{2} }[/math]There exists an explicit solution for [math]\displaystyle{ \mathbf {\hat {w}} }[/math] which minimizes the squared error: [math]\displaystyle{ {\mathbf {\hat {w}}}=({\mathbf {X}}{\mathbf {X}}^{T})^{-1}{\mathbf {X}}{\mathbf {y}} }[/math], where [math]\displaystyle{ {\mathbf {X}} }[/math] is the matrix whose columns are the training inputs, and [math]\displaystyle{ {\mathbf {y}} }[/math] is the vector of training outputs. Then, the model can make predictions on new inputs: [math]\displaystyle{ {\hat {y}}({\mathbf {x}})={\mathbf {\hat {w}}}\cdot {\mathbf {x}} }[/math].

However, this result can be rewritten as: [math]\displaystyle{ {\hat {y}}({\mathbf {x}})=({\mathbf {x}}^{T}{\mathbf {X}})({\mathbf {X}}^{T}{\mathbf {X}})^{-1}{\mathbf {y}} }[/math]. Note that this dual solution is expressed solely in terms of the inner products between inputs. This motivates extending linear regression to settings in which, instead of directly taking inner products between inputs, we first transform the inputs according to a chosen feature map and then evaluate the inner products between the transformed inputs. As discussed above, this can be captured by a kernel function [math]\displaystyle{ K({\mathbf {x}},{\mathbf {x}}') }[/math], since all kernel functions are inner products of feature-mapped inputs. This yields the ridgeless kernel regression estimator:[math]\displaystyle{ {\hat {y}}({\mathbf {x}})=K({\mathbf {x}},{\mathbf {X}})\;K({\mathbf {X}},{\mathbf {X}})^{-1}\;{\mathbf {y}}. }[/math]If the kernel matrix [math]\displaystyle{ K({\mathbf {X}},{\mathbf {X}}) }[/math] is singular, one uses the Moore-Penrose pseudoinverse. The regression equations are called "ridgeless" because they lack a ridge regularization term.

In this view, linear regression is a special case of kernel regression with the identity feature map: [math]\displaystyle{ \psi ({\mathbf {x}})={\mathbf {x}} }[/math]. Equivalently, kernel regression is simply linear regression in the feature space (i.e. the range of the feature map defined by the chosen kernel). Note that kernel regression is typically a nonlinear regression in the input space, which is a major strength of the algorithm.

Just as it’s possible to perform linear regression using iterative optimization algorithms such as gradient descent, one can perform kernel regression using kernel gradient descent. This is equivalent to performing gradient descent in the feature space. It’s known that if the weight vector is initialized close to zero, least-squares gradient descent converges to the minimum-norm solution, i.e., the final weight vector has the minimum Euclidean norm of all the interpolating solutions. In the same way, kernel gradient descent yields the minimum-norm solution with respect to the RKHS norm. This is an example of the implicit regularization of gradient descent.

The NTK gives a rigorous connection between the inference performed by infinite-width ANNs and that performed by kernel methods: when the loss function is the least-squares loss, the inference performed by an ANN is in expectation equal to ridgeless kernel regression with respect to the NTK. This suggests that the performance of large ANNs in the NTK parametrization can be replicated by kernel methods for suitably chosen kernels.

Overparametrization, interpolation, and generalization

In overparametrized models, the number of tunable parameters exceeds the number of training samples. In this case, the model is able to memorize (perfectly fit) the training data. Therefore, overparametrized models interpolate the training data, achieving essentially zero training error.

Modern overparametrized models achieve low generalization error despite having the capacity to interpolate (memorize) the training set. This phenomenon can be understood by studying the generalization properties of high-dimensional kernel regression.

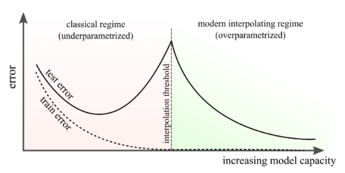
Kernel regression is typically viewed as a non-parametric learning algorithm, since there are no explicit parameters to tune once a kernel function has been chosen. An alternate view is to recall that kernel regression is simply linear regression in feature space, so the “effective” number of parameters is the dimension of the feature space. Therefore, studying kernels with high-dimensional feature maps can provide insights about strongly overparametrized models.

As an example, consider the problem of generalization. According to classical statistics, memorization should cause models to fit noisy signals in the training data, harming their performance on unseen data. To mitigate this, machine learning algorithms often introduce regularization to mitigate noise-fitting tendencies. Surprisingly, modern neural networks (which tend to be strongly overparametrized) seem to generalize well, even in the absence of explicit regularization. To study the generalization properties of overparametrized neural networks, one can exploit the infinite-width duality with ridgeless kernel regression. Recent works have derived equations describing the expected generalization error of high-dimensional kernel regression; these results immediately explain the generalization of sufficiently wide neural networks trained to convergence on least-squares.

Convergence to a global minimum

For a convex loss functional [math]\displaystyle{ {\mathcal {C}} }[/math] with a global minimum, if the NTK remains positive-definite during training, the loss of the ANN [math]\displaystyle{ {\mathcal {C}}\left(f\left(\cdot;\theta \left(t\right)\right)\right) }[/math] converges to that minimum as [math]\displaystyle{ t\to \infty }[/math]. This positive-definiteness property has been shown in a number of cases, yielding the first proofs that large-width ANNs converge to global minima during training.

Extensions and limitations

The NTK can be studied for various ANN architectures, in particular convolutional neural networks (CNNs), recurrent neural networks (RNNs) and transformers. In such settings, the large-width limit corresponds to letting the number of parameters grow, while keeping the number of layers fixed: for CNNs, this involves letting the number of channels grow.

Individual parameters of a wide neural network in the kernel regime change negligibly during training. However, this implies that infinite-width neural networks cannot exhibit feature learning, which is widely considered to be an important property of realistic deep neural networks. This is not a generic feature of infinite-width neural networks and is largely due to a specific choice of the scaling by which the width is taken to the infinite limit; indeed several works have found alternate infinite-width scaling limits of neural networks in which there is no duality with kernel regression and feature learning occurs during training. Others introduce a "neural tangent hierarchy" to describe finite-width effects, which may drive feature learning.

Neural Tangents is a free and open-source Python library used for computing and doing inference with the infinite width NTK and neural network Gaussian process (NNGP) corresponding to various common ANN architectures. In addition, there exists a scikit-learn compatible implementation of the infinite width NTK for Gaussian processes called scikit-ntk.

Details

When optimizing the parameters [math]\displaystyle{ \theta\in\mathbb{R}^{P} }[/math] of an ANN to minimize an empirical loss through gradient descent, the NTK governs the dynamics of the ANN output function [math]\displaystyle{ f_{\theta} }[/math] throughout the training.

Case 1: Scalar output

An ANN with scalar output consists of a family of functions [math]\displaystyle{ f\left(\cdot,\theta\right):\mathbb{R}^{n_{\mathrm{in}}}\to\mathbb{R} }[/math] parametrized by a vector of parameters [math]\displaystyle{ \theta\in\mathbb{R}^{P} }[/math].

The NTK is a kernel [math]\displaystyle{ \Theta:\mathbb{R}^{n_{\mathrm{in}}}\times\mathbb{R}^{n_{\mathrm{in}}}\to\mathbb{R} }[/math] defined by[math]\displaystyle{ \Theta\left(x,y;\theta\right)=\sum_{p=1}^{P}\partial_{\theta_{p}}f\left(x;\theta\right)\partial_{\theta_{p}}f\left(y;\theta\right). }[/math]In the language of kernel methods, the NTK [math]\displaystyle{ \Theta }[/math] is the kernel associated with the feature map [math]\displaystyle{ \left(x\mapsto\partial_{\theta_{p}}f\left(x;\theta\right)\right)_{p=1,\ldots,P} }[/math]. To see how this kernel drives the training dynamics of the ANN, consider a dataset [math]\displaystyle{ \left(x_{i}\right)_{i=1,\ldots,n}\subset\mathbb{R}^{n_{\mathrm{in}}} }[/math] with scalar labels [math]\displaystyle{ \left(z_{i}\right)_{i=1,\ldots,n}\subset\mathbb{R} }[/math] and a loss function [math]\displaystyle{ c:\mathbb{R}\times\mathbb{R}\to\mathbb{R} }[/math]. Then the associated empirical loss, defined on functions [math]\displaystyle{ f:\mathbb{R}^{n_{\mathrm{in}}}\to\mathbb{R} }[/math], is given by[math]\displaystyle{ \mathcal{C}\left(f\right)=\sum_{i=1}^{n}c\left(f\left(x_{i}\right),z_{i}\right). }[/math]When the ANN [math]\displaystyle{ f\left(\cdot;\theta\right):\mathbb{R}^{n_{\mathrm{in}}}\to\mathbb{R} }[/math] is trained to fit the dataset (i.e. minimize [math]\displaystyle{ \mathcal{C} }[/math]) via continuous-time gradient descent, the parameters [math]\displaystyle{ \left(\theta\left(t\right)\right)_{t\geq0} }[/math] evolve through the ordinary differential equation:

[math]\displaystyle{ \partial_{t}\theta\left(t\right)=-\nabla\mathcal{C}\left(f\left(\cdot;\theta\right)\right). }[/math]

During training the ANN output function follows an evolution differential equation given in terms of the NTK:

[math]\displaystyle{ \partial_{t}f\left(x;\theta\left(t\right)\right)=-\sum_{i=1}^{n}\Theta\left(x,x_{i};\theta\right)\partial_{w}c\left(w,z_{i}\right)\Big|_{w=f\left(x_{i};\theta\left(t\right)\right)}. }[/math]

This equation shows how the NTK drives the dynamics of [math]\displaystyle{ f\left(\cdot;\theta\left(t\right)\right) }[/math] in the space of functions [math]\displaystyle{ \mathbb{R}^{n_{\mathrm{in}}}\to\mathbb{R} }[/math] during training.

Case 2: Vector output

An ANN with vector output of size [math]\displaystyle{ n_{\mathrm{out}} }[/math] consists in a family of functions [math]\displaystyle{ f\left(\cdot;\theta\right):\mathbb{R}^{n_{\mathrm{in}}}\to\mathbb{R}^{n_{\mathrm{out}}} }[/math] parametrized by a vector of parameters [math]\displaystyle{ \theta\in\mathbb{R}^{P} }[/math].

In this case, the NTK [math]\displaystyle{ \Theta:\mathbb{R}^{n_{\mathrm{in}}}\times\mathbb{R}^{n_{\mathrm{in}}}\to\mathcal{M}_{n_{\mathrm{out}}}\left(\mathbb{R}\right) }[/math] is a matrix-valued kernel, with values in the space of [math]\displaystyle{ n_{\mathrm{out}}\times n_{\mathrm{out}} }[/math] matrices, defined by[math]\displaystyle{ \Theta_{k,l}\left(x,y;\theta\right)=\sum_{p=1}^{P}\partial_{\theta_{p}}f_{k}\left(x;\theta\right)\partial_{\theta_{p}}f_{l}\left(y;\theta\right). }[/math]Empirical risk minimization proceeds as in the scalar case, with the difference being that the loss function takes vector inputs [math]\displaystyle{ c:\mathbb{R}^{n_{\mathrm{out}}}\times\mathbb{R}^{n_{\mathrm{out}}}\to\mathbb{R} }[/math]. The training of [math]\displaystyle{ f_{\theta\left(t\right)} }[/math] through continuous-time gradient descent yields the following evolution in function space driven by the NTK:[math]\displaystyle{ \partial_{t}f_{k}\left(x;\theta\left(t\right)\right)=-\sum_{i=1}^{n}\sum_{l=1}^{n_{\mathrm{out}}}\Theta_{k,l}\left(x,x_{i};\theta\right)\partial_{w_{l}}c\left(\left(w_{1},\ldots,w_{n_{\mathrm{out}}}\right),z_{i}\right)\Big|_{w=f\left(x_{i};\theta\left(t\right)\right)}. }[/math]This generalizes the equation shown in case 1 for scalar outputs.

Interpretation

Each data point [math]\displaystyle{ x_{i} }[/math] influences the evolution, of the output [math]\displaystyle{ f\left(x;\theta\right) }[/math] for each input [math]\displaystyle{ x }[/math], throughout the training. More concretely, with respect to example [math]\displaystyle{ i }[/math], the NTK value [math]\displaystyle{ \Theta\left(x,x_{i};\theta\right) }[/math] determines the influence of the loss gradient [math]\displaystyle{ \partial_{w}c\left(w,z_{i}\right)\big|_{w=f\left(x_{i};\theta\right)} }[/math] on the evolution of ANN output [math]\displaystyle{ f\left(x;\theta\right) }[/math] through a gradient descent step. In the scalar case, this reads[math]\displaystyle{ f\left(x;\theta\left(t+\epsilon\right)\right)-f\left(x;\theta\left(t\right)\right)\approx\epsilon\sum_{i=1}^{n}\Theta\left(x,x_{i};\theta\left(t\right)\right)\partial_{w}c\left(w,z_{i}\right)\big|_{w=f\left(x_{i};\theta\right)}. }[/math]

Wide fully-connected ANNs have a deterministic NTK, which remains constant throughout training

Consider an ANN with fully-connected layers [math]\displaystyle{ \ell=0,\ldots,L }[/math] of widths [math]\displaystyle{ n_{0}=n_{\mathrm{in}},n_{1},\ldots,n_{L}=n_{\mathrm{out}} }[/math], so that [math]\displaystyle{ f\left(\cdot;\theta\right)=R_{L-1}\circ\cdots\circ R_{0} }[/math], where [math]\displaystyle{ R_{\ell}=\sigma\circ A_{\ell} }[/math] is the composition of an affine transformation [math]\displaystyle{ A_{i} }[/math] with the pointwise application of a nonlinearity [math]\displaystyle{ \sigma:\mathbb{R}\to\mathbb{R} }[/math], where [math]\displaystyle{ \theta }[/math] parametrizes the maps [math]\displaystyle{ A_{0},\ldots,A_{L-1} }[/math]. The parameters [math]\displaystyle{ \theta\in\mathbb{R}^{P} }[/math] are initialized randomly, in an independent, identically distributed way.

As the widths grow, the NTK's scale is affected by the exact parametrization of the [math]\displaystyle{ A_{i} }[/math]'s and by the parameter initialization. This motivates the so-called NTK parametrization [math]\displaystyle{ A_{\ell}\left(x\right)=\frac{1}{\sqrt{n_{\ell}}}W^{\left(\ell\right)}x+b^{\left(\ell\right)} }[/math]. This parametrization ensures that if the parameters [math]\displaystyle{ \theta\in\mathbb{R}^{P} }[/math] are initialized as standard normal variables, the NTK has a finite nontrivial limit. In the large-width limit, the NTK converges to a deterministic (non-random) limit [math]\displaystyle{ \Theta_{\infty} }[/math], which stays constant in time.

The NTK [math]\displaystyle{ \Theta_{\infty} }[/math] is explicitly given by [math]\displaystyle{ \Theta_{\infty}=\Theta^{\left(L\right)} }[/math], where [math]\displaystyle{ \Theta^{\left(L\right)} }[/math] is determined by the set of recursive equations:

[math]\displaystyle{ \begin{align} \Theta^{\left(1\right)}\left(x,y\right) &= \Sigma^{\left(1\right)}\left(x,y\right),\\ \Sigma^{\left(1\right)}\left(x,y\right) &= \frac{1}{n_{\mathrm{in}}}x^{T}y+1,\\ \Theta^{\left(\ell+1\right)}\left(x,y\right) &=\Theta^{\left(\ell\right)}\left(x,y\right)\dot{\Sigma}^{\left(\ell+1\right)}\left(x,y\right)+\Sigma^{\left(\ell+1\right)}\left(x,y\right),\\ \Sigma^{\left(\ell+1\right)}\left(x,y\right) &= L_{\Sigma^{\left(\ell\right)}}^{\sigma}\left(x,y\right),\\ \dot{\Sigma}^{\left(\ell+1\right)}\left(x,y\right) &= L_{\Sigma^{\left(\ell\right)}}^{\dot{\sigma}}, \end{align} }[/math]

where [math]\displaystyle{ L_{K}^{f} }[/math] denotes the kernel defined in terms of the Gaussian expectation:

[math]\displaystyle{ L_{K}^{f}\left(x,y\right)=\mathbb{E}_{\left(X,Y\right)\sim\mathcal{N}\left(0,\begin{pmatrix}K\left(x,x\right) & K\left(x,y\right)\\ K\left(y,x\right) & K\left(y,y\right) \end{pmatrix}\right)}\left[f\left(X\right)f\left(Y\right)\right]. }[/math]

In this formula the kernels [math]\displaystyle{ \Sigma^{\left(\ell\right)} }[/math] are the ANN's so-called activation kernels.

Wide fully connected networks are linear in their parameters throughout training

The NTK describes the evolution of neural networks under gradient descent in function space. Dual to this perspective is an understanding of how neural networks evolve in parameter space, since the NTK is defined in terms of the gradient of the ANN's outputs with respect to its parameters. In the infinite width limit, the connection between these two perspectives becomes especially interesting. The NTK remaining constant throughout training at large widths co-occurs with the ANN being well described throughout training by its first order Taylor expansion around its parameters at initialization:

[math]\displaystyle{ f\left(x;\theta(t)\right) = f\left(x;\theta(0)\right) + \nabla_{\theta}f\left(x;\theta(0)\right) \left(\theta(t) - \theta(0)\right) + \mathcal{O}\left(\min\left(n_1 \dots n_{L-1}\right)^{-\frac{1}{2}}\right) . }[/math]

See also

• Large width limits of neural networks

External links

• Ananthaswamy, Anil (2021-10-11). "A New Link to an Old Model Could Crack the Mystery of Deep Learning". https://www.quantamagazine.org/a-new-link-to-an-old-model-could-crack-the-mystery-of-deep-learning-20211011/.