Omega constant

The omega constant is a mathematical constant defined as the unique real number that satisfies the equation

[math]\displaystyle{ \Omega e^\Omega = 1. }[/math]

It is the value of W(1), where W is Lambert's W function. The name is derived from the alternate name for Lambert's W function, the omega function. The numerical value of Ω is given by

Ω = 0.567143290409783872999968662210... (sequence A030178 in the OEIS).

1/Ω = 1.763222834351896710225201776951... (sequence A030797 in the OEIS).

Properties

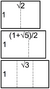
Fixed point representation

The defining identity can be expressed, for example, as

[math]\displaystyle{ \ln(\tfrac{1}{\Omega})=\Omega. }[/math]

or

[math]\displaystyle{ -\ln(\Omega)=\Omega }[/math]

as well as

[math]\displaystyle{ e^{-\Omega}= \Omega. }[/math]

Computation

One can calculate Ω iteratively, by starting with an initial guess Ω₀, and considering the sequence

[math]\displaystyle{ \Omega_{n+1}=e^{-\Omega_n}. }[/math]

This sequence will converge to Ω as n approaches infinity. This is because Ω is an attractive fixed point of the function e^−x.

It is much more efficient to use the iteration

[math]\displaystyle{ \Omega_{n+1}=\frac{1+\Omega_n}{1+e^{\Omega_n}}, }[/math]

because the function

[math]\displaystyle{ f(x)=\frac{1+x}{1+e^x}, }[/math]

in addition to having the same fixed point, also has a derivative that vanishes there. This guarantees quadratic convergence; that is, the number of correct digits is roughly doubled with each iteration.

Using Halley's method, Ω can be approximated with cubic convergence (the number of correct digits is roughly tripled with each iteration): (see also Lambert W function § Numerical evaluation).

[math]\displaystyle{ \Omega_{j+1}=\Omega_j-\frac{\Omega_j e^{\Omega_j}-1}{e^{\Omega_j}(\Omega_j+1)-\frac{(\Omega_j+2)(\Omega_je^{\Omega_j}-1)}{2\Omega_j+2}}. }[/math]

Integral representations

An identity due to Victor Adamchik is given by the relationship

[math]\displaystyle{ \int_{-\infty}^\infty\frac{dt}{(e^t-t)^2+\pi^2} = \frac{1}{1+\Omega}. }[/math]

Other relations due to Mező and Kalugin-Jeffrey-Corless are:

[math]\displaystyle{ \Omega=\frac{1}{\pi}\operatorname{Re}\int_0^\pi\log\left(\frac{e^{e^{it}}-e^{-it}}{e^{e^{it}}-e^{it}}\right) dt, }[/math]

[math]\displaystyle{ \Omega=\frac{1}{\pi}\int_0^\pi\log\left(1+\frac{\sin t}{t}e^{t\cot t}\right)dt. }[/math]

The latter two identities can be extended to other values of the W function (see also Lambert W function § Representations).

Transcendence

The constant Ω is transcendental. This can be seen as a direct consequence of the Lindemann–Weierstrass theorem. For a contradiction, suppose that Ω is algebraic. By the theorem, e^−Ω is transcendental, but Ω = e^−Ω, which is a contradiction. Therefore, it must be transcendental.

External links

• Weisstein, Eric W.. "Omega Constant". http://mathworld.wolfram.com/OmegaConstant.html. 
• "Omega constant (1,000,000 digits)", Darkside communication group (in Japan), http://ankokudan.org/d/d.htm?mathlistindex-e.html, retrieved 2017-12-25