Great icosahedron
Template:Reg star polyhedron stat table File:Great icosahedron.stl
In geometry, the great icosahedron is one of four Kepler–Poinsot polyhedra (nonconvex regular polyhedra), with Schläfli symbol {3,5⁄2} and Coxeter-Dynkin diagram of ![]()
![]()
![]()
![]()
![]()
![]()
![]() . It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence.
. It is composed of 20 intersecting triangular faces, having five triangles meeting at each vertex in a pentagrammic sequence.
The great icosahedron can be constructed analogously to the pentagram, its two-dimensional analogue, via the extension of the (n–1)-dimensional simplex faces of the core n-polytope (equilateral triangles for the great icosahedron, and line segments for the pentagram) until the figure regains regular faces. The grand 600-cell can be seen as its four-dimensional analogue using the same process.
Construction
The edge length of a great icosahedron is [math]\displaystyle{ \frac{7+3\sqrt{5}}{2} }[/math] times that of the original icosahedron.
Images
| Transparent model | Density | Stellation diagram | Net |
|---|---|---|---|
 A transparent model of the great icosahedron (See also Animation) |
 It has a density of 7, as shown in this cross-section. |
 It is a stellation of the icosahedron, counted by Wenninger as model [W41] and the 16th of 17 stellations of the icosahedron and 7th of 59 stellations by Coxeter. |
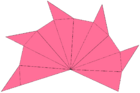 × 12 × 12Net (surface geometry); twelve isosceles pentagrammic pyramids, arranged like the faces of a dodecahedron. Each pyramid folds up like a fan: the dotted lines fold the opposite direction from the solid lines. |
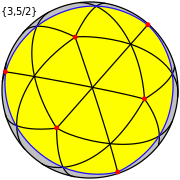 This polyhedron represents a spherical tiling with a density of 7. (One spherical triangle face is shown above, outlined in blue, filled in yellow) |
As a snub
The great icosahedron can be constructed as a uniform snub, with different colored faces and only tetrahedral symmetry: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . This construction can be called a retrosnub tetrahedron or retrosnub tetratetrahedron,[1] similar to the snub tetrahedron symmetry of the icosahedron, as a partial faceting of the truncated octahedron (or omnitruncated tetrahedron):
. This construction can be called a retrosnub tetrahedron or retrosnub tetratetrahedron,[1] similar to the snub tetrahedron symmetry of the icosahedron, as a partial faceting of the truncated octahedron (or omnitruncated tetrahedron): ![]()
![]()
![]()
![]()
![]() . It can also be constructed with 2 colors of triangles and pyritohedral symmetry as,
. It can also be constructed with 2 colors of triangles and pyritohedral symmetry as, ![]()
![]()
![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , and is called a retrosnub octahedron.
, and is called a retrosnub octahedron.
| Tetrahedral | Pyritohedral |
|---|---|

|

|
Related polyhedra
It shares the same vertex arrangement as the regular convex icosahedron. It also shares the same edge arrangement as the small stellated dodecahedron.
A truncation operation, repeatedly applied to the great icosahedron, produces a sequence of uniform polyhedra. Truncating edges down to points produces the great icosidodecahedron as a rectified great icosahedron. The process completes as a birectification, reducing the original faces down to points, and producing the great stellated dodecahedron.
The truncated great stellated dodecahedron is a degenerate polyhedron, with 20 triangular faces from the truncated vertices, and 12 (hidden) doubled up pentagonal faces ({10/2}) as truncations of the original pentagram faces, the latter forming two great dodecahedra inscribed within and sharing the edges of the icosahedron.
| Name | Great stellated dodecahedron |
Truncated great stellated dodecahedron | Great icosidodecahedron |
Truncated great icosahedron |
Great icosahedron |
|---|---|---|---|---|---|
| Coxeter-Dynkin diagram |
|||||
| Picture | 
|

|

|
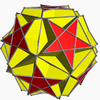
|

|
References
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. (1999). The fifty-nine icosahedra (3rd ed.). Tarquin. ISBN 978-1-899618-32-3 (1st Edn University of Toronto (1938))
- H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN:0-486-61480-8, 3.6 6.2 Stellating the Platonic solids, pp. 96–104
External links
 |


