Great truncated icosidodecahedron
This article needs editing for compliance with Wikipedia's Manual of Style. In particular, it has problems with MOS:RADICAL. (June 2022) (Learn how and when to remove this template message) |
| Great truncated icosidodecahedron | |
|---|---|
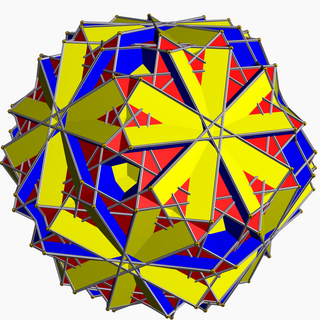
| |
| Type | Uniform star polyhedron |
| Elements | F = 62, E = 180 V = 120 (χ = 2) |
| Faces by sides | 30{4}+20{6}+12{10/3} |
| Wythoff symbol | 2 3 5/3 | |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U68, C87, W108 |
| Dual polyhedron | Great disdyakis triacontahedron |
| Vertex figure | 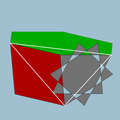 4.6.10/3 |
| Bowers acronym | Gaquatid |
File:Great truncated icosidodecahedron.stl
In geometry, the great truncated icosidodecahedron (or great quasitruncated icosidodecahedron or stellatruncated icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U68. It has 62 faces (30 squares, 20 hexagons, and 12 decagrams), 180 edges, and 120 vertices.[1] It is given a Schläfli symbol t0,1,2{5⁄3,3}, and Coxeter-Dynkin diagram, ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Cartesian coordinates
Cartesian coordinates for the vertices of a great truncated icosidodecahedron centered at the origin are all the even permutations of [math]\displaystyle{ \begin{array}{ccclc} \Bigl(& \pm\,\varphi,& \pm\,\varphi,& \pm \bigl[3-\frac{1}{\varphi}\bigr] &\Bigr),\\ \Bigl(& \pm\,2\varphi,& \pm\,\frac{1}{\varphi},& \pm\,\frac{1}{\varphi^3} &\Bigl), \\ \Bigl(& \pm\,\varphi,& \pm\,\frac{1}{\varphi^2},& \pm \bigl[1+\frac{3}{\varphi}\bigr] &\Bigr), \\ \Bigl(& \pm\,\sqrt{5},& \pm\,2,& \pm\,\frac{\sqrt{5}}{\varphi} &\Bigr), \\ \Bigl(& \pm\,\frac{1}{\varphi},& \pm\,3,& \pm\,\frac{2}{\varphi} &\Bigr), \end{array} }[/math]
where [math]\displaystyle{ \varphi = \tfrac{1 + \sqrt 5}{2} }[/math] is the golden ratio.
Related polyhedra
Great disdyakis triacontahedron
| Great disdyakis triacontahedron | |
|---|---|

| |
| Type | Star polyhedron |
| Face | 
|
| Elements | F = 120, E = 180 V = 62 (χ = 2) |
| Symmetry group | Ih, [5,3], *532 |
| Index references | DU68 |
| dual polyhedron | Great truncated icosidodecahedron |
File:Great disdyakis triacontahedron.stl The great disdyakis triacontahedron (or trisdyakis icosahedron) is a nonconvex isohedral polyhedron. It is the dual of the great truncated icosidodecahedron. Its faces are triangles.
Proportions
The triangles have one angle of [math]\displaystyle{ \arccos\left(\tfrac{1}{6}+\tfrac{1}{15}\sqrt{5}\right) \approx 71.594\,636\,220\,88^{\circ} }[/math], one of [math]\displaystyle{ \arccos\left(\tfrac{3}{4}+\tfrac{1}{10}\sqrt{5}\right) \approx 13.192\,999\,040\,74^{\circ} }[/math] and one of [math]\displaystyle{ \arccos\left(\tfrac{3}{8}-\tfrac{5}{24}\sqrt{5}\right) \approx 95.212\,364\,738\,38^{\circ}. }[/math] The dihedral angle equals [math]\displaystyle{ \arccos\left(\tfrac{-179+24\sqrt{5}}{241}\right) \approx 121.336\,250\,807\,39^{\circ}. }[/math] Part of each triangle lies within the solid, hence is invisible in solid models.
See also
References
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5 p. 96
External links
- Weisstein, Eric W.. "Great truncated icosidodecahedron". http://mathworld.wolfram.com/GreatTruncatedIcosidodecahedron.html.
- Weisstein, Eric W.. "Great disdyakis triacontahedron". http://mathworld.wolfram.com/GreatDisdyakisTriacontahedron.html.
 |

