Snub dodecadodecahedron
| Snub dodecadodecahedron | |
|---|---|
| |
| Type | Uniform star polyhedron |
| Elements | F = 84, E = 150 V = 60 (χ = −6) |
| Faces by sides | 60{3}+12{5}+12{5/2} |
| Wythoff symbol | | 2 5/2 5 |
| Symmetry group | I, [5,3]+, 532 |
| Index references | U40, C49, W111 |
| Dual polyhedron | Medial pentagonal hexecontahedron |
| Vertex figure | 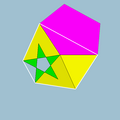 3.3.5/2.3.5 |
| Bowers acronym | Siddid |
File:Snub dodecadodecahedron.stl
In geometry, the snub dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U40. It has 84 faces (60 triangles, 12 pentagons, and 12 pentagrams), 150 edges, and 60 vertices.[1] It is given a Schläfli symbol sr{5⁄2,5}, as a snub great dodecahedron.
Cartesian coordinates
Cartesian coordinates for the vertices of an inverted snub dodecadodecahedron are all the even permutations of [math]\displaystyle{ \begin{array}{crrrc} \Bigl(& \pm\,2\alpha\ ,& \pm\,2\ ,& \pm\,2\beta\ & \Bigr), \\[2pt] \Bigl(& \pm \bigl[\alpha+\frac{\beta}{\varphi} + \varphi\bigr],& \pm \bigl[-\alpha\varphi + \beta + \frac{1}{\varphi}\bigr],& \pm \bigl[\frac{\alpha}{\varphi} + \beta\varphi - 1\bigr] & \Bigr), \\[2pt] \Bigl(& \pm \bigl[-\frac{\alpha}{\varphi} + \beta\varphi + 1\bigr],& \pm \bigl[-\alpha + \frac{\beta}{\varphi} - \varphi\bigr],& \pm \bigl[\alpha\varphi + \beta - \frac{1}{\varphi}\bigr] & \Bigr), \\[2pt] \Bigl(& \pm \bigl[-\frac{\alpha}{\varphi} + \beta\varphi - 1\bigr],& \pm \bigl[\alpha - \frac{\beta}{\varphi} - \varphi\bigr],& \pm \bigl[\alpha\varphi + \beta + \frac{1}{\varphi}\bigr] & \Bigr), \\[2pt] \Bigl(& \pm \bigl[\alpha + \frac{\beta}{\varphi} - \varphi\bigr],& \pm \bigl[\alpha\varphi - \beta + \frac{1}{\varphi}\bigr],& \pm \bigl[\frac{\alpha}{\varphi} + \beta\varphi + 1\bigr] & \Bigr), \end{array} }[/math]
with an even number of plus signs, where [math]\displaystyle{ \beta = \frac{\ \ \frac{\alpha^2}{\varphi} + \varphi \ \ }{\ \alpha\varphi - \frac{1}{\varphi}}\ , }[/math] [math]\displaystyle{ \varphi = \tfrac{1+\sqrt 5}{2} }[/math] is the golden ratio, and α is the positive real root of [math]\displaystyle{ \varphi\alpha^4 - \alpha^3 + 2\alpha^2 - \alpha - \frac{1}{\varphi} \quad \implies \quad \alpha \approx 0.7964421. }[/math] Taking the odd permutations of the above coordinates with an odd number of plus signs gives another form, the enantiomorph of the other one. Taking α to be the negative root gives the inverted snub dodecadodecahedron.
Related polyhedra
Medial pentagonal hexecontahedron
| Medial pentagonal hexecontahedron | |
|---|---|
| |
| Type | Star polyhedron |
| Face | 
|
| Elements | F = 60, E = 150 V = 84 (χ = −6) |
| Symmetry group | I, [5,3]+, 532 |
| Index references | DU40 |
| dual polyhedron | Snub dodecadodecahedron |
File:Medial pentagonal hexecontahedron.stl The medial pentagonal hexecontahedron is a nonconvex isohedral polyhedron. It is the dual of the snub dodecadodecahedron. It has 60 intersecting irregular pentagonal faces.
See also
References
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5
External links
- Weisstein, Eric W.. "Medial pentagonal hexecontahedron". http://mathworld.wolfram.com/MedialPentagonalHexecontahedron.html.
- Weisstein, Eric W.. "Snub dodecadodecahedron". http://mathworld.wolfram.com/SnubDodecadodecahedron.html.
 |  |
