Physics:Angle-resolved low-coherence interferometry

From HandWiki

Angle-resolved low-coherence interferometry (a/LCI) is an emerging[when?] biomedical imaging technology which uses the properties of scattered light to measure the average size of cell structures, including cell nuclei. The technology shows promise as a clinical tool for in situ detection of dysplastic, or precancerous tissue.

Introduction

A/LCI combines low-coherence interferometry with angle-resolved scattering to solve the inverse problem of determining scatterer geometry based on far field diffraction patterns. Similar to optical coherence domain reflectometry (OCDR) and optical coherence tomography (OCT), a/LCI uses a broadband light source in an interferometry scheme in order to achieve optical sectioning with a depth resolution set by the coherence length of the source. Angle-resolved scattering measurements capture light as a function of the scattering angle, and invert the angles to deduce the average size of the scattering objects via a computational light scattering model such as Mie theory, which predicts angles based on the size of the scattering sphere. Combining these techniques allows construction of a system that can measure average scatter size at various depths within a tissue sample.

At present the most significant medical application of the technology is determining the state of tissue health based on measurements of average cell nuclei size. It has been found that as tissue changes from normal to cancerous, the average cell nuclei size increases.[1] Several recent studies[2] have shown that via cell nuclei measurements, a/LCI can detect the presence of low- and high-grade dysplasia with 91% sensitivity and distinguish between normal and dysplastic with 97% specificity.

History

Since 2000, light scattering systems have been used for biomedical applications such as the study of cellular morphology[3] as well as the diagnosis of dysplasia.[4] Variations in scattering distributions as a function of angle or wavelength have been used to deduce information regarding the size of cells and subcellular objects such as nuclei and organelles. These size measurements can then be used diagnostically to detect tissue changes—including neoplastic changes (those leading to cancer).

Light scattering spectroscopy has been used to detect dysplasia in the colon, bladder, cervix, and esophagus of human patients.[2] Light scattering has also been used to detect Barrett's esophagus, a metaplastic condition with a high probability of leading to dysplasia.[5]

However, in contrast with a/LCI, these techniques all rely on total intensity based measurements, which lack the ability to provide results as a function of depth in the tissue.

Early a/LCI models

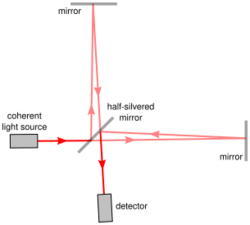
Path of light in a Michelson interferometer.

The first implementation of a/LCI[6] used a Michelson interferometer, the same model used in the famous Michelson–Morley experiment. The Michelson interferometer splits one beam of light into two paths, one reference path and one sampling path, and recombines them again to produce a waveform resulting from interference. The difference between the reference beam and the sampling beam thus reveal the properties of the sample in the way it scatters light.

The early a/LCI device used a movable mirror and lens in the reference arm so that researchers could replicate different angles and depths in the reference beam as they occurred in the collected backscattered light. This allowed isolation of the backscattered light at varying depths of reflection in the sample. In order to transform the data into measurements of cell structure, angular scattering distributions are then compared to the predictions of Mie theory—which calculates the size of spheres relative to their light scattering patterns.

The a/LCI technique was first validated in studies of polystyrene microspheres,[6] the sizes of which were known and relatively homogeneous. A later study expanded the signal processing method to compensate for the nonspherical and inhomogeneous nature of cell nuclei.[7]

This early system required up to 40 minutes to acquire the data for a 1 mm² point in a sample, but proved the feasibility of the idea.

Fourier-domain implementation

Like OCT, the early implementations of a/LCI relied on physically changing the optical path length (OPL) to control the depth in the sample from which data are acquired. However, it has been demonstrated[8] that it is possible to use a Fourier domain implementation to yield depth resolution in a single data acquisition. A broadband light source is used to produce a spectrum of wavelengths at once, and the backscattered light is collected by a coherent optical fiber in the return path to capture different scattering angles simultaneously.[9] Intensity is then measured via a spectrometer: a single frame from the spectrometer contains scattering intensity as a function of wavelength and angle. Finally the data is Fourier transformed on a line-by-line basis to generate scattering intensity as a function of OPL and angle. In the resulting image, the x axis represents the OPL and the y axis the angle of reflection, thus yielding a 2D map of reflection intensities.

Using this method, the acquisition speed is limited only by the integration time of the spectrometer and can be as short at 20 ms. The same data that initially required tens of minutes to acquire can be acquired ~105 times faster.[9]

Schematic description

Schematic of a/LCI system. Light is provided by SLD, sample and reference light are generated by fiber splitter (FS), while lenses L2, L3, and L4 provide collimation. The beamsplitter (BS) combines sample and reference arm light, which is then incident on the imaging spectrometer. On the right is the optical geometry of probe tip with illumination fiber (DF), lens L1, and collection fiber (FB).

The Fourier-domain version of the a/LCI system uses a superluminescent diode (SLD) with a fiber-coupled output as the light source. A fiber splitter separates the signal path at 90% intensity and the reference path at 10%.

The light from the SLD passes through an optical isolator and subsequently a polarization controller. It has been shown that control of light polarization is important for maximizing optical signal and comparing angular scattering with the Mie scattering model.[10] A polarization-maintaining fiber is used to carry the illumination light to the sample. A second polarization controller is similarly used to control the polarization of the light passing through the reference path.

The output of the fiber on the right is collimated using lens L1 and illuminates the tissue. But because the delivery fiber is offset from the optical axis of the lens, the beam is delivered to the sample at an oblique angle. Backscattered light is then collimated by the same lens and collected by the fiber bundle. The fibers are one focal length from the lens, and the sample is one focal length on the other side. This configuration captures light from the maximum range of angles and minimizes light noise due to specular reflections.

At the distal end of the fiber bundle, light from each fiber is imaged onto the spectrometer. Light from the sample and reference arms are mixed by a beamsplitting cube (BS), and are incident on the entrance slit of an imaging spectrometer. Data from the imaging spectrometer are transferred to a computer via USB interface for signal processing and display of results. The computer also provides control of the imaging spectrometer.

Clinical device prototype

Picture of portable a/LCI system with handheld fiber probe on the right and the optical engine on the left. The computer is not shown.

The a/LCI system has recently been enhanced to allow operation in a clinical setting with the addition of a handheld wand.[11] By carefully controlling the polarization in the delivery fiber, using polarization-maintaining fibers and inline polarizers, the new system allows manipulation of the handheld wand without signal degradation due to birefringence effects. In addition, the new system employed an anti-reflection coated ball lens in the probe tip, which reduces reflections that otherwise limit the depth range of the system.

The portable system uses a 2 ft by 2 ft optical breadboard as the base, with the source, fiber optic components, lens, beamsplitter, and imaging spectrometer mounted to the breadboard. An aluminum cover protects the optics. A fiber probe with a handheld probe enables easy access to tissue samples for testing. On the left side sits a white sample platform, where tissue is placed for testing. The handheld probe is used by the operator to select specific sites on the tissue from which a/LCI readings are acquired.

See also

References

  1. ↑ Pyhtila, J; Chalut, K; Boyer, J; Keener, J; Damico, T; Gottfried, M; Gress, F; Wax, A (2007). "In situ detection of nuclear atypia in Barrett's esophagus by using angle-resolved low-coherence interferometry". Gastrointestinal Endoscopy 65 (3): 487–91. doi:10.1016/j.gie.2006.10.016. PMID 17321252. 
  2. ↑ 2.0 2.1 Wax, Adam; Pyhtila, John W.; Graf, Robert N.; Nines, Ronald; Boone, Charles W.; Dasari, Ramachandra R.; Feld, Michael S.; Steele, Vernon E. et al. (2005). "Prospective grading of neoplastic change in rat esophagus epithelium using angle-resolved low-coherence interferometry". Journal of Biomedical Optics 10 (5): 051604. doi:10.1117/1.2102767. PMID 16292952. Bibcode: 2005JBO....10e1604W. 
  3. ↑ Backman, V.; Gopal, V.; Kalashnikov, M.; Badizadegan, K.; Gurjar, R.; Wax, A.; Georgakoudi, I.; Mueller, M. et al. (2001). "Measuring cellular structure at submicrometer scale with light scattering spectroscopy". IEEE Journal of Selected Topics in Quantum Electronics 7 (6): 887–893. doi:10.1109/2944.983289. Bibcode: 2001IJSTQ...7..887B. 
  4. ↑ Wallace, M; Perelman, LT; Backman, V; Crawford, JM; Fitzmaurice, M; Seiler, M; Badizadegan, K; Shields, SJ et al. (2000). "Endoscopic Detection of Dysplasia in Patients with Barrett's Esophagus Using Light-Scattering Spectroscopy". Gastroenterology 119 (3): 677–82. doi:10.1053/gast.2000.16511. PMID 10982761. 
  5. ↑ Lovat, Laurence B.; Pickard, David; Novelli, Marco; Ripley, Paul M.; Francis, Helen; Bigio, Irving J.; Bown, Stephen G. (2000-04-01). "4919 A novel optical biopsy technique using elastic scattering spectroscopy for dysplasia and cancer in Barrett's esophagus." (in English). Gastrointestinal Endoscopy 51 (4): AB227. doi:10.1016/S0016-5107(00)14616-4. ISSN 0016-5107. https://www.giejournal.org/article/S0016-5107(00)14616-4/abstract. 
  6. ↑ 6.0 6.1 Wax, A; Yang, C; Backman, V; Kalashnikov, M; Dasari, RR; Feld, MS (2002). "Determination of particle size by using the angular distribution of backscattered light as measured with low-coherence interferometry". Journal of the Optical Society of America A 19 (4): 737–44. doi:10.1364/JOSAA.19.000737. PMID 11934166. Bibcode: 2002JOSAA..19..737W. https://authors.library.caltech.edu/3340/1/WAXjosaa02.pdf. 
  7. ↑ Wax, A; Yang, C; Backman, V; Badizadegan, K; Boone, CW; Dasari, RR; Feld, MS (2002). "Cellular organization and substructure measured using angle-resolved low-coherence interferometry". Biophysical Journal 82 (4): 2256–64. doi:10.1016/S0006-3495(02)75571-9. PMID 11916880. Bibcode: 2002BpJ....82.2256W. 
  8. ↑ Choma, M; Sarunic, M; Yang, C; Izatt, J (2003). "Sensitivity advantage of swept source and Fourier domain optical coherence tomography". Optics Express 11 (18): 2183–9. doi:10.1364/OE.11.002183. PMID 19466106. Bibcode: 2003OExpr..11.2183C. http://authors.library.caltech.edu/3312/01/CHOoe03.pdf. 
  9. ↑ 9.0 9.1 Pyhtila, John W.; Boyer, Jeffrey D.; Chalut, Kevin J.; Wax, Adam (2006). "Fourier-domain angle-resolved low coherence interferometry through an endoscopic fiber bundle for light-scattering spectroscopy". Optics Letters 31 (6): 772–4. doi:10.1364/OL.31.000772. PMID 16544619. Bibcode: 2006OptL...31..772P. 
  10. ↑ Pyhtila, John W.; Wax, Adam (2007). "Polarization effects on scatterer sizing accuracy analyzed with frequency-domain angle-resolved low-coherence interferometry". Applied Optics 46 (10): 1735–41. doi:10.1364/AO.46.001735. PMID 17356616. Bibcode: 2007ApOpt..46.1735P. 
  11. ↑ "Oncoscope". http://www.oncoscope.com. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Angle-resolved_low-coherence_interferometry&oldid=3284842"