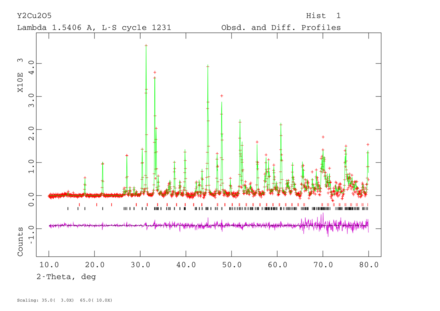
Physics:Powder diffraction

Powder diffraction is a scientific technique using X-ray, neutron, or electron diffraction on powder or microcrystalline samples for structural characterization of materials.[2] An instrument dedicated to performing such powder measurements is called a powder diffractometer.
Powder diffraction stands in contrast to single crystal diffraction techniques, which work best with a single, well-ordered crystal.[3]
Explanation
The most common type of powder diffraction is with X-rays, the focus of this article, although some aspects of neutron powder diffraction are mentioned. (Powder electron diffraction is more complex due to dynamical diffraction[4] and is not discussed further herein.) Typical diffractometers use electromagnetic radiation (waves) with known wavelength and frequency, which is determined by their source. The source is often X-rays, and neutrons are also common sources, with their frequency determined by their de Broglie wavelength. When these waves reach the sample, the incoming beam is either reflected off the surface, or can enter the lattice and be diffracted by the atoms present in the sample. If the atoms are arranged symmetrically with a separation distance d, these waves will interfere constructively only where the path-length difference 2d sin θ is equal to an integer multiple of the wavelength, producing a diffraction maximum in accordance with Bragg's law. These waves interfere destructively at points between the intersections where the waves are out of phase, and do not lead to bright spots in the diffraction pattern.[5] Because the sample itself is acting as the diffraction grating, this spacing is the atomic spacing.
The distinction between powder and single crystal diffraction is the degree of texturing in the sample. Single crystals have maximal texturing, and are said to be anisotropic. In contrast, in powder diffraction, every possible crystalline orientation is represented equally in a powdered sample, the isotropic case. Powder X-ray diffraction (PXRD) operates under the assumption that the sample is randomly arranged. Therefore, a statistically significant number of each plane of the crystal structure will be in the proper orientation to diffract the X-rays. Therefore, each plane will be represented in the signal. In practice, it is sometimes necessary to rotate the sample orientation to eliminate the effects of texturing and achieve true randomness.
Mathematically, crystals can be described by a Bravais lattice with some regularity in the spacing between atoms. Because of this regularity, we can describe this structure in a different way using the reciprocal lattice, which is related to the original structure by a Fourier transform. This three-dimensional space can be described with reciprocal axes x*, y*, and z* or alternatively in spherical coordinates q, φ*, and χ*. In powder diffraction, intensity is homogeneous over φ* and χ*, and only q remains as an important measurable quantity. This is because orientational averaging causes the three-dimensional reciprocal space that is studied in single crystal diffraction to be projected onto a single dimension.
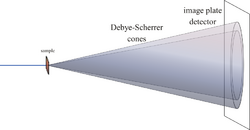
When the scattered radiation is collected on a flat plate detector, the rotational averaging leads to smooth diffraction rings around the beam axis, rather than the discrete Laue spots observed in single crystal diffraction. The angle between the beam axis and the ring is called the scattering angle and in X-ray crystallography always denoted as 2θ (in scattering of visible light the convention is usually to call it θ). In accordance with Bragg's law, each ring corresponds to a particular reciprocal lattice vector G in the sample crystal. This leads to the definition of the scattering vector as:
In this equation, G is the reciprocal lattice vector, q is the length of the reciprocal lattice vector, k is the momentum transfer vector, θ is half of the scattering angle, and λ is the wavelength of the source. Powder diffraction data are usually presented as a diffractogram in which the diffracted intensity, I, is shown as a function either of the scattering angle 2θ or as a function of the scattering vector length q. The latter variable has the advantage that the diffractogram no longer depends on the value of the wavelength λ. The advent of synchrotron sources has widened the choice of wavelength considerably. To facilitate comparability of data obtained with different wavelengths the use of q is therefore recommended and gaining acceptability.
Uses
Relative to other methods of analysis, powder diffraction allows for rapid, non-destructive analysis of multi-component mixtures without the need for extensive sample preparation.[7] This gives laboratories the ability to quickly analyze unknown materials and perform materials characterization in such fields as metallurgy, mineralogy, chemistry, forensic science, archeology, condensed matter physics, and the biological and pharmaceutical sciences. Identification is performed by comparison of the diffraction pattern to a known standard or to a database such as the International Centre for Diffraction Data's Powder Diffraction File (PDF) or the Cambridge Structural Database (CSD). Advances in hardware and software, particularly improved optics and fast detectors, have dramatically improved the analytical capability of the technique, especially relative to the speed of the analysis. The fundamental physics upon which the technique is based provides high precision and accuracy in the measurement of interplanar spacings, sometimes to fractions of an Ångström, resulting in authoritative identification frequently used in patents, criminal cases and other areas of law enforcement. The ability to analyze multiphase materials also allows analysis of how materials interact in a particular matrix such as a pharmaceutical tablet, a circuit board, a mechanical weld, a geologic core sampling, cement and concrete, or a pigment found in an historic painting. The method has been historically used for the identification and classification of minerals, but it can be used for nearly any material, even amorphous ones, so long as a suitable reference pattern is known or can be constructed.
Phase identification
The most widespread use of powder diffraction is in the identification and characterization of crystalline solids, each of which produces a distinctive diffraction pattern. Both the positions (corresponding to lattice spacings) and the relative intensity of the lines in a diffraction pattern are indicative of a particular phase and material, providing a "fingerprint" for comparison. A multi-phase mixture, e.g. a soil sample, will show more than one pattern superposed, allowing for the determination of the relative concentrations of phases in the mixture.
J.D. Hanawalt, an analytical chemist who worked for Dow Chemical in the 1930s, was the first to realize the analytical potential of creating a database. Today it is represented by the Powder Diffraction File (PDF) of the International Centre for Diffraction Data (formerly Joint Committee for Powder Diffraction Studies). This has been made searchable by computer through the work of global software developers and equipment manufacturers. There are now over 1,047,661 reference materials in the 2021 Powder Diffraction File Databases, and these databases are interfaced to a wide variety of diffraction analysis software and distributed globally. The Powder Diffraction File contains many subfiles, such as minerals, metals and alloys, pharmaceuticals, forensics, excipients, superconductors, semiconductors, etc., with large collections of organic, organometallic and inorganic reference materials.
Crystallinity
In contrast to a crystalline pattern consisting of a series of sharp peaks, amorphous materials (liquids, glasses etc.) produce a broad background signal. Many polymers show semicrystalline behavior, i.e. part of the material forms an ordered crystallite by folding of the molecule. A single polymer molecule may well be folded into two different, adjacent crystallites and thus form a tie between the two. The tie part is prevented from crystallizing. The result is that the crystallinity will never reach 100%. Powder XRD can be used to determine the crystallinity by comparing the integrated intensity of the background pattern to that of the sharp peaks. Values obtained from powder XRD are typically comparable but not quite identical to those obtained from other methods such as DSC.
Lattice parameters
The position of a diffraction peak is independent of the atomic positions within the cell and entirely determined by the size and shape of the unit cell of the crystalline phase. Each peak represents a certain lattice plane and can therefore be characterized by a Miller index. If the symmetry is high, e.g.: cubic or hexagonal it is usually not too hard to identify the index of each peak, even for an unknown phase. This is particularly important in solid-state chemistry, where one is interested in finding and identifying new materials. Once a pattern has been indexed, this characterizes the reaction product and identifies it as a new solid phase. Indexing programs exist to deal with the harder cases, but if the unit cell is very large and the symmetry low (triclinic) success is not always guaranteed.
Expansion tensors, bulk modulus
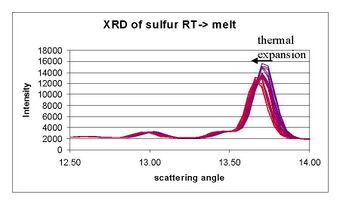
Cell parameters are somewhat temperature and pressure dependent. Powder diffraction can be combined with in situ temperature and pressure control. As these thermodynamic variables are changed, the observed diffraction peaks will migrate continuously to indicate higher or lower lattice spacings as the unit cell distorts. This allows for measurement of such quantities as the thermal expansion tensor and the isothermal bulk modulus, as well determination of the full equation of state of the material.
Phase transitions
At some critical set of conditions, for example 0 °C for water at 1 atm, a new arrangement of atoms or molecules may become stable, leading to a phase transition. At this point new diffraction peaks will appear or old ones disappear according to the symmetry of the new phase. If the material melts to an isotropic liquid, all sharp lines will disappear and be replaced by a broad amorphous pattern. If the transition produces another crystalline phase, one set of lines will suddenly be replaced by another set. In some cases however lines will split or coalesce, e.g. if the material undergoes a continuous, second order phase transition. In such cases the symmetry may change because the existing structure is distorted rather than replaced by a completely different one. For example, the diffraction peaks for the lattice planes (100) and (001) can be found at two different values of q for a tetragonal phase, but if the symmetry becomes cubic the two peaks will come to coincide.
Crystal structure refinement and determination
Crystal structure determination from powder diffraction data is extremely challenging due to the overlap of reflections in a powder experiment. A number of different methods exist for structural determination, such as simulated annealing and charge flipping. The crystal structures of known materials can be refined, i.e. as a function of temperature or pressure, using the Rietveld method.[8] The Rietveld method is a so-called full pattern analysis technique. A crystal structure, together with instrumental and microstructural information, is used to generate a theoretical diffraction pattern that can be compared to the observed data. A least squares procedure is then used to minimize the difference between the calculated pattern and each point of the observed pattern by adjusting model parameters. Techniques to determine unknown structures from powder data do exist, but are somewhat specialized.[9] A number of programs that can be used in structure determination are TOPAS, Fox, DASH, GSAS-II, EXPO2004, and a few others. As alternative to the Rietveld method, machine learning algorithms have been applied to crystals structure classification based on powder diffraction.[10][11]
Size and strain broadening
There are many factors that determine the width B of a diffraction peak. These include:
- instrumental factors
- the presence of defects to the perfect lattice
- differences in strain in different grains
- the size of the crystallites
It is often possible to separate the effects of size and strain. When size broadening is independent of q (K = 1/d), strain broadening increases with increasing q-values. In most cases there will be both size and strain broadening. It is possible to separate these by combining the two equations in what is known as the Hall–Williamson method:
Thus, when we plot vs. we get a straight line with slope and intercept .
The expression is a combination of the Scherrer equation for size broadening and the Stokes and Wilson expression for strain broadening. The value of η is the strain in the crystallites, the value of D represents the size of the crystallites. The constant k is typically close to unity and ranges from 0.8 to 1.39.
Comparison of X-ray and neutron scattering
X-ray photons scatter by interaction with the electron cloud of the material, neutrons are scattered by the nuclei. This means that, in the presence of heavy atoms with many electrons, it may be difficult to detect light atoms by X-ray diffraction. In contrast, the neutron scattering lengths of most atoms are approximately equal in magnitude. Neutron diffraction techniques may therefore be used to detect light elements such as oxygen or hydrogen in combination with heavy atoms. The neutron diffraction technique therefore has obvious applications to problems such as determining oxygen displacements in materials like high temperature superconductors and ferroelectrics, or to hydrogen bonding in biological systems.
A further complication in the case of neutron scattering from hydrogenous materials is the strong incoherent scattering of hydrogen (80.27(6) barn). This leads to a very high background in neutron diffraction experiments, and may make structural investigations impossible. A common solution is deuteration, i.e., replacing the 1-H atoms in the sample with deuterium (2-H). The incoherent scattering length of deuterium is much smaller (2.05(3) barn) making structural investigations significantly easier. However, in some systems, replacing hydrogen with deuterium may alter the structural and dynamic properties of interest.
As neutrons also have a magnetic moment, they are additionally scattered by any magnetic moments in a sample. In the case of long range magnetic order, this leads to the appearance of new Bragg reflections. In most simple cases, powder diffraction may be used to determine the size of the moments and their spatial orientation.
Aperiodically arranged clusters
Predicting the scattered intensity in powder diffraction patterns from gases, liquids, and randomly distributed nano-clusters in the solid state[12] is (to first order) done rather elegantly with the Debye scattering equation:[13]
where the magnitude of the scattering vector q is in reciprocal lattice distance units, N is the number of atoms, fi(q) is the atomic scattering factor for atom i and scattering vector q, while rij is the distance between atom i and atom j. One can also use this to predict the effect of nano-crystallite shape on detected diffraction peaks, even if in some directions the cluster is only one atom thick.
Semi-quantitative analysis
Semi-quantitative analysis of polycrystalline mixtures can be performed by using traditional single-peaks methods such as the Relative Intensity Ratio (RIR) or whole-pattern methods using Rietveld Refinement or PONKCS (Partial Or No Known Crystal Structures) method. The use of each method depends on the knowledge on the analyzed system, given that, for instance, Rietveld refinement needs the solved crystal structure of each component of the mixture to be performed. In the last decades, multivariate analysis begun spreading as an alternative method for phase quantification.[14][15]
Devices
Cameras
The simplest cameras for X-ray powder diffraction consist of a small capillary and either a flat plate detector (originally a piece of X-ray film, now more and more a flat-plate detector or a CCD-camera) or a cylindrical one (originally a piece of film in a cookie-jar, but increasingly bent position sensitive detectors are used). The two types of cameras are known as the Laue and the Debye–Scherrer camera.
In order to ensure complete powder averaging, the capillary is usually spun around its axis.
For neutron diffraction vanadium cylinders are used as sample holders. Vanadium has a negligible absorption and coherent scattering cross section for neutrons and is hence nearly invisible in a powder diffraction experiment. Vanadium does however have a considerable incoherent scattering cross section which may cause problems for more sensitive techniques such as neutron inelastic scattering.
A later development in X-ray cameras is the Guinier camera. It is built around a focusing bent crystal monochromator. The sample is usually placed in the focusing beam, e.g. as a dusting on a piece of sticky tape. A cylindrical piece of film (or electronic multichannel detector) is put on the focusing circle, but the incident beam prevented from reaching the detector to prevent damage from its high intensity.
Cameras based on hybrid photon counting technology, such as the PILATUS detector, are widely used in applications where high data acquisition speeds and increased data quality are required.[16]
Diffractometers
Diffractometers can be operated both in transmission and reflection, but reflection is more common. The powder sample is loaded in a small disc-like container and its surface carefully flattened. The disc is put on one axis of the diffractometer and tilted by an angle θ while a detector (scintillation counter) rotates around it on an arm at twice this angle. This configuration is known under the name Bragg–Brentano θ-2θ.
Another configuration is the Bragg–Brentano θ-θ configuration in which the sample is stationary while the X-ray tube and the detector are rotated around it. The angle formed between the X-ray source and the detector is 2θ. This configuration is most convenient for loose powders.
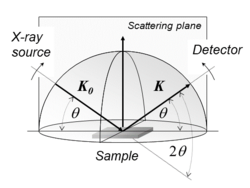
Diffractometer settings for different experiments can schematically be illustrated by a hemisphere, in which the powder sample resides in the origin. The case of recording a pattern in the Bragg-Brentano θ-θ mode is shown in the figure, where K0 and K stand for the wave vectors of the incoming and diffracted beam that both make up the scattering plane. Various other settings for texture or stress/strain measurements can also be visualized with this graphical approach.[17]
Position-sensitive detectors (PSD) and area detectors, which allow collection from multiple angles at once, are becoming more popular on currently supplied instrumentation.
Neutron diffraction
Sources that produce a neutron beam of suitable intensity and speed for diffraction are only available at a small number of research reactors and spallation sources in the world. Angle dispersive (fixed wavelength) instruments typically have a battery of individual detectors arranged in a cylindrical fashion around the sample holder, and can therefore collect scattered intensity simultaneously on a large 2θ range. Time of flight instruments normally have a small range of banks at different scattering angles which collect data at varying resolutions.
X-ray tubes

Laboratory X-ray diffraction equipment relies on the use of an X-ray tube, which is used to produce the X-rays. The most commonly used laboratory X-ray tube uses a copper anode, but cobalt and molybdenum are also popular. The wavelength in nm varies for each source. The table below shows these wavelengths, published by Bearden in 1967[18] (all values in nm):
| Element | Kα (weight average) |
Kα2 (strong) |
Kα1 (very strong) |
Kβ (weak) |
|---|---|---|---|---|
| Cr | 0.229100 | 0.229361 | 0.228970 | 0.208487 |
| Fe | 0.193736 | 0.193998 | 0.193604 | 0.175661 |
| Co | 0.179026 | 0.179285 | 0.178897 | 0.162079 |
| Cu | 0.154184 | 0.154439 | 0.154056 | 0.139222 |
| Mo | 0.071073 | 0.071359 | 0.070930 | 0.063229 |
According to the last re-examination of Hölzer et al. (1997),[19] and quoted in the International Tables for Crystallography[20] these values are respectively:
| Element | Kα2 | Kα1 | Kβ |
|---|---|---|---|
| Cr | 0.2293651 | 0.2289726 | 0.2084881 |
| Co | 0.1792835 | 0.1788996 | 0.1620826 |
| Cu | 0.15444274 | 0.15405929 | 0.1392234 |
| Mo | 0.0713607 | 0.070931715 | 0.0632303 |
Other sources
In-house applications of X-ray diffraction has always been limited to the relatively few wavelengths shown in the table above. The available choice was much needed because the combination of certain wavelengths and certain elements present in a sample can lead to strong fluorescence which increases the background in the diffraction pattern. A notorious example is the presence of iron in a sample when using copper radiation. In general elements just below the anode element in the periodic table need to be avoided.
Another limitation is that the intensity of traditional generators is relatively low, requiring lengthy exposure times and precluding any time dependent measurement. The advent of synchrotron sources has drastically changed this picture and caused powder diffraction methods to enter a whole new phase of development. Not only is there a much wider choice of wavelengths available, the high brilliance of the synchrotron radiation makes it possible to observe changes in the pattern during chemical reactions, temperature ramps, changes in pressure and the like.
The tunability of the wavelength also makes it possible to observe anomalous scattering effects when the wavelength is chosen close to the absorption edge of one of the elements of the sample.
Neutron diffraction has never been an in house technique because it requires the availability of an intense neutron beam only available at a nuclear reactor or spallation source. Typically the available neutron flux, and the weak interaction between neutrons and matter, require relative large samples.
Advantages and disadvantages
Although it is possible to solve crystal structures from powder X-ray data alone, its single crystal analogue is a far more powerful technique for structure determination. This is directly related to the fact that information is lost by the collapse of the 3D space onto a 1D axis. Nevertheless, powder X-ray diffraction is a powerful and useful technique in its own right. It is mostly used to characterize and identify phases, and to refine details of an already known structure, rather than solving unknown structures.
Advantages of the technique are:
- simplicity of sample preparation
- rapidity of measurement
- the ability to analyze mixed phases, e.g. soil samples
- "in situ" structure determination
By contrast growth and mounting of large single crystals is notoriously difficult. In fact there are many materials for which, despite many attempts, it has not proven possible to obtain single crystals. Many materials are readily available with sufficient microcrystallinity for powder diffraction, or samples may be easily ground from larger crystals. In the field of solid-state chemistry that often aims at synthesizing new materials, single crystals thereof are typically not immediately available. Powder diffraction is therefore one of the most powerful methods to identify and characterize new materials in this field.
Particularly for neutron diffraction, which requires larger samples than X-ray diffraction due to a relatively weak scattering cross section, the ability to use large samples can be critical, although newer and more brilliant neutron sources are being built that may change this picture.
Since all possible crystal orientations are measured simultaneously, collection times can be quite short even for small and weakly scattering samples. This is not merely convenient, but can be essential for samples which are unstable either inherently or under X-ray or neutron bombardment, or for time-resolved studies. For the latter it is desirable to have a strong radiation source. The advent of synchrotron radiation and modern neutron sources has therefore done much to revitalize the powder diffraction field because it is now possible to study temperature dependent changes, reaction kinetics and so forth by means of time-resolved powder diffraction.
See also
- Bragg diffraction
- Condensed matter physics
- Crystallographic database
- Crystallography
- Diffractometer
- Electron crystallography
- Electron diffraction
- Materials science
- Metallurgy
- Neutron diffraction
- Pair distribution function
- Solid state chemistry
- Texture (crystalline)
- Ultrafast x-ray
- X-ray crystallography
- X-ray scattering techniques
References
- ↑ P. Fraundorf; Shuhan Lin (2004). "Spiral powder overlays". Microscopy and Microanalysis 10 (S02): 1356–1357. doi:10.1017/S1431927604884034. Bibcode: 2004MiMic..10S1356F.
- ↑ B.D. Cullity Elements of X-ray Diffraction Addison Wesley Mass. 1978 ISBN 0-201-01174-3
- ↑ Clegg, William; Blake, Alexander J; Cole, Jacqueline M; Evans, John S O; Main, Peter; Parsons, Simon; Watkin, David J (2009-06-18). "Chaper 17. Powder diffraction". Crystal Structure Analysis. Oxford University Press. pp. 251–270. doi:10.1093/acprof:oso/9780199219469.003.0017. ISBN 978-0-19-921946-9. http://www.oxfordscholarship.com/view/10.1093/acprof:oso/9780199219469.001.0001/acprof-9780199219469.
- ↑ Cowley, J. M. (1995). Diffraction physics (3rd ed.). Amsterdam: Elsevier Science B.V. ISBN 978-0-444-82218-5. OCLC 162131289.
- ↑ Klug, Harold; Alexander, Leroy (1954). X-ray diffraction Procedures (2nd ed.). Canada: John Wiley & Sons, Inc.. p. 122. ISBN 978-0-471-49369-3. https://archive.org/details/xraydiffractionp00klug.
- ↑ Liss, Klaus-Dieter; Bartels, Arno; Schreyer, Andreas; Clemens, Helmut (2003). "High-Energy X-Rays: A tool for Advanced Bulk Investigations in Materials Science and Physics". Textures and Microstructures 35 (3–4): 219. doi:10.1080/07303300310001634952.
- ↑ B.D. Cullity Elements of X-ray diffraction Addison–Wesley, 1978 ISBN 0-201-01174-3 Chapter 14
- ↑ Rietveld, H. M. (1969). "A profile refinement method for nuclear and magnetic structures". Journal of Applied Crystallography 2 (2): 65–75. doi:10.1107/S0021889869006558. Bibcode: 1969JApCr...2...65R. https://doi.org/10.1107/S0021889869006558.
- ↑ Structure determination form powder diffraction data IUCr Monographs on crystallography, Edt. W.I.F. David, K. Shankland, L.B. McCusker and Ch. Baerlocher. 2002. Oxford Science publications ISBN 0-19-850091-2
- ↑ Vecsei, Pascal Marc; Choo, Kenny; Chang, Johan; Neupert, Titus (2019). "Neural network based classification of crystal symmetries from x-ray diffraction patterns". Physical Review B 99 (24). doi:10.1103/PhysRevB.99.245120. Bibcode: 2019PhRvB..99x5120V. https://doi.org/10.1103/PhysRevB.99.245120.
- ↑ Park, Woon Bae; Chung, Jiyoung; Jung, Jaeyoung; Sohn, Keemin; Pal Singh, Satendra; Pro, Myoungho; Shin, Namsoo; Sohn, Kee-Sun (2017). "Classification of crystal structure using a convolutional neural network". IUCrJ 4 (4): 486–494. doi:10.1107/S205225251700714X. PMID 28875035. PMC 5571811. Bibcode: 2017IUCrJ...4..486P. https://doi.org/10.1107/S205225251700714X.
- ↑ B. E. Warren (1969/1990) X-ray diffraction (Addison–Wesley, Reading MA/Dover, Mineola NY) ISBN 0-486-66317-5.
- ↑ Debye, P. (1915). "Zerstreuung von Röntgenstrahlen". Annalen der Physik 351 (6): 809. doi:10.1002/andp.19153510606. Bibcode: 1915AnP...351..809D. https://zenodo.org/record/1447297.
- ↑ Guccione, Pietro; Lopresti, Mattia; Milanesio, Marco; Caliandro, Rocco (December 2020). "Multivariate Analysis Applications in X-ray Diffraction". Crystals 11 (1): 12. doi:10.3390/cryst11010012. Bibcode: 2020Cryst..11...12G.
- ↑ Lopresti, M.; Mangolini, B.; Milanesio, M.; Caliandro, R.; Palin, L. (1 August 2022). "Multivariate versus traditional quantitative phase analysis of X-ray powder diffraction and fluorescence data of mixtures showing preferred orientation and microabsorption". Journal of Applied Crystallography 55 (4): 837–850. doi:10.1107/S1600576722004708. PMID 35974739. Bibcode: 2022JApCr..55..837L.
- ↑ Šišak Jung, D; Donath, T; Magdysyuk, O; Bednarcik, J (2017). "High-energy X-ray applications: Current status and new opportunities". Powder Diffraction, 32(S2) 32 (S2): 22–27. doi:10.1017/S0885715617001191. Bibcode: 2017PDiff..32S..22S.
- ↑ 17.0 17.1 M. Birkholz (2005). Thin Film Analysis by X-Ray Scattering. Wiley-VCH. ISBN 978-3-527-31052-4. https://www.wiley.com/en-mx/Thin+Film+Analysis+by+X+Ray+Scattering-p-9783527310524.
- ↑ Bearden, J. A. (1967). "X-Ray Wavelengths". Reviews of Modern Physics 39 (1): 78–124. doi:10.1103/RevModPhys.39.78. Bibcode: 1967RvMP...39...78B.
- ↑ Hölzer, G.; Fritsch, M.; Deutsch, M.; Härtwig, J.; Förster, E. (1997-12-01). "Kα1,2 and Kβ1,3 x-ray emission lines of the 3d transition metals". Physical Review A 56 (6): 4554–4568. doi:10.1103/PhysRevA.56.4554. Bibcode: 1997PhRvA..56.4554H.
- ↑ Deslattes, R.D.; Kessler Jr, E.G.; Indelicato, P.; Lindroth, E. (2006), "Table 4.2.2.1. K-series reference wavelengths in Å", in Prince, E., International Tables for Crystallography, C, International Union of Crystallography, pp. 203, https://onlinelibrary.wiley.com/iucr/itc/Cb/ch4o2v0001/table4o2o2o1/
Further reading
- Gilmore, C.J.; Kaduk, J.A.; Schenk, H., eds (2019). International Tables for Crystallography - Volume H: Powder Diffraction. Wiley. ISBN 978-1-118-41628-0. https://it.iucr.org/H/.
External links
 |