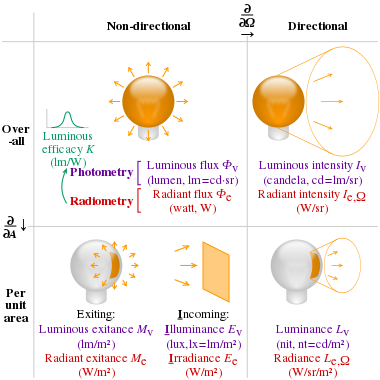
Physics:Radiant exitance
In radiometry, radiant exitance or radiant emittance is the radiant flux emitted by a surface per unit area, whereas spectral exitance or spectral emittance is the radiant exitance of a surface per unit frequency or wavelength, depending on whether the spectrum is taken as a function of frequency or of wavelength. This is the emitted component of radiosity. The SI unit of radiant exitance is the watt per square metre (W/m2), while that of spectral exitance in frequency is the watt per square metre per hertz (W·m−2·Hz−1) and that of spectral exitance in wavelength is the watt per square metre per metre (W·m−3)—commonly the watt per square metre per nanometre (W·m−2·nm−1). The CGS unit erg per square centimeter per second (erg·cm−2·s−1) is often used in astronomy. Radiant exitance is often called "intensity" in branches of physics other than radiometry, but in radiometry this usage leads to confusion with radiant intensity.
Mathematical definitions
Radiant exitance
Radiant exitance of a surface, denoted Me ("e" for "energetic", to avoid confusion with photometric quantities), is defined as[1] [math]\displaystyle{ M_\mathrm{e} = \frac{\partial \Phi_\mathrm{e}}{\partial A}, }[/math] where ∂ is the partial derivative symbol, Φe is the radiant flux emitted, and A is the surface area.
If we want to talk about the radiant flux received by a surface, we speak of irradiance.
The radiant exitance of a black surface, according to the Stefan–Boltzmann law, is equal to: [math]\displaystyle{ M_\mathrm{e}^\circ = \sigma T^4, }[/math] where σ is the Stefan–Boltzmann constant, and T is the temperature of that surface. For a real surface, the radiant exitance is equal to: [math]\displaystyle{ M_\mathrm{e} = \varepsilon M_\mathrm{e}^\circ = \varepsilon \sigma T^4, }[/math] where ε is the emissivity of that surface.
Spectral exitance
Spectral exitance in frequency of a surface, denoted Me,ν, is defined as[1]
- [math]\displaystyle{ M_{\mathrm{e},\nu} = \frac{\partial M_\mathrm{e}}{\partial \nu}, }[/math]
where ν is the frequency.
Spectral exitance in wavelength of a surface, denoted Me,λ, is defined as[1] [math]\displaystyle{ M_{\mathrm{e},\lambda} = \frac{\partial M_\mathrm{e}}{\partial \lambda}, }[/math] where λ is the wavelength.
The spectral exitance of a black surface around a given frequency or wavelength, according to the Lambert's cosine law and the Planck's law, is equal to:
- [math]\displaystyle{ \begin{align} M_{\mathrm{e},\nu}^\circ & = \pi L_{\mathrm{e},\Omega,\nu}^\circ = \frac{2\pi h\nu^3}{c^2} \frac{1}{e^\frac{h\nu}{kT} - 1}, \\[8pt] M_{\mathrm{e},\lambda}^\circ & = \pi L_{\mathrm{e},\Omega,\lambda}^\circ = \frac{2\pi hc^2}{\lambda^5} \frac{1}{e^\frac{hc}{\lambda kT} - 1}, \end{align} }[/math]
where h is the Planck constant, ν is the frequency, λ is the wavelength, k is the Boltzmann constant, c is the speed of light in the medium, T is the temperature of that surface. For a real surface, the spectral exitance is equal to: [math]\displaystyle{ \begin{align} M_{\mathrm{e},\nu} & = \varepsilon M_{\mathrm{e},\nu}^\circ = \frac{2\pi h\varepsilon \nu^3}{c^2} \frac{1}{e^\frac{h\nu}{kT} - 1}, \\[8pt] M_{\mathrm{e},\lambda} & = \varepsilon M_{\mathrm{e},\lambda}^\circ = \frac{2\pi h\varepsilon c^2}{\lambda^5} \frac{1}{e^\frac{hc}{\lambda kT} - 1}. \end{align} }[/math]
SI radiometry units
| Quantity | Unit | Dimension | Notes | |||||
|---|---|---|---|---|---|---|---|---|
| Name | Symbol[nb 1] | Name | Symbol | Symbol | ||||
| Radiant energy | Qe[nb 2] | joule | J | M⋅L2⋅T−2 | Energy of electromagnetic radiation. | |||
| Radiant energy density | we | joule per cubic metre | J/m3 | M⋅L−1⋅T−2 | Radiant energy per unit volume. | |||
| Radiant flux | Φe[nb 2] | watt | W = J/s | M⋅L2⋅T−3 | Radiant energy emitted, reflected, transmitted or received, per unit time. This is sometimes also called "radiant power". | |||
| Spectral flux | Φe,ν[nb 3] | watt per hertz | W/Hz | M⋅L2⋅T−2 | Radiant flux per unit frequency or wavelength. The latter is commonly measured in W⋅nm−1. | |||
| Φe,λ[nb 4] | watt per metre | W/m | M⋅L⋅T−3 | |||||
| Radiant intensity | Ie,Ω[nb 5] | watt per steradian | W/sr | M⋅L2⋅T−3 | Radiant flux emitted, reflected, transmitted or received, per unit solid angle. This is a directional quantity. | |||
| Spectral intensity | Ie,Ω,ν[nb 3] | watt per steradian per hertz | W⋅sr−1⋅Hz−1 | M⋅L2⋅T−2 | Radiant intensity per unit frequency or wavelength. The latter is commonly measured in W⋅sr−1⋅nm−1. This is a directional quantity. | |||
| Ie,Ω,λ[nb 4] | watt per steradian per metre | W⋅sr−1⋅m−1 | M⋅L⋅T−3 | |||||
| Radiance | Le,Ω[nb 5] | watt per steradian per square metre | W⋅sr−1⋅m−2 | M⋅T−3 | Radiant flux emitted, reflected, transmitted or received by a surface, per unit solid angle per unit projected area. This is a directional quantity. This is sometimes also confusingly called "intensity". | |||
| Spectral radiance | Le,Ω,ν[nb 3] | watt per steradian per square metre per hertz | W⋅sr−1⋅m−2⋅Hz−1 | M⋅T−2 | Radiance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅sr−1⋅m−2⋅nm−1. This is a directional quantity. This is sometimes also confusingly called "spectral intensity". | |||
| Le,Ω,λ[nb 4] | watt per steradian per square metre, per metre | W⋅sr−1⋅m−3 | M⋅L−1⋅T−3 | |||||
| Irradiance Flux density |
Ee[nb 2] | watt per square metre | W/m2 | M⋅T−3 | Radiant flux received by a surface per unit area. This is sometimes also confusingly called "intensity". | |||
| Spectral irradiance Spectral flux density |
Ee,ν[nb 3] | watt per square metre per hertz | W⋅m−2⋅Hz−1 | M⋅T−2 | Irradiance of a surface per unit frequency or wavelength. This is sometimes also confusingly called "spectral intensity". Non-SI units of spectral flux density include jansky (1 Jy = 10−26 W⋅m−2⋅Hz−1) and solar flux unit (1 sfu = 10−22 W⋅m−2⋅Hz−1 = 104 Jy). | |||
| Ee,λ[nb 4] | watt per square metre, per metre | W/m3 | M⋅L−1⋅T−3 | |||||
| Radiosity | Je[nb 2] | watt per square metre | W/m2 | M⋅T−3 | Radiant flux leaving (emitted, reflected and transmitted by) a surface per unit area. This is sometimes also confusingly called "intensity". | |||
| Spectral radiosity | Je,ν[nb 3] | watt per square metre per hertz | W⋅m−2⋅Hz−1 | M⋅T−2 | Radiosity of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m−2⋅nm−1. This is sometimes also confusingly called "spectral intensity". | |||
| Je,λ[nb 4] | watt per square metre, per metre | W/m3 | M⋅L−1⋅T−3 | |||||
| Radiant exitance | Me[nb 2] | watt per square metre | W/m2 | M⋅T−3 | Radiant flux emitted by a surface per unit area. This is the emitted component of radiosity. "Radiant emittance" is an old term for this quantity. This is sometimes also confusingly called "intensity". | |||
| Spectral exitance | Me,ν[nb 3] | watt per square metre per hertz | W⋅m−2⋅Hz−1 | M⋅T−2 | Radiant exitance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m−2⋅nm−1. "Spectral emittance" is an old term for this quantity. This is sometimes also confusingly called "spectral intensity". | |||
| Me,λ[nb 4] | watt per square metre, per metre | W/m3 | M⋅L−1⋅T−3 | |||||
| Radiant exposure | He | joule per square metre | J/m2 | M⋅T−2 | Radiant energy received by a surface per unit area, or equivalently irradiance of a surface integrated over time of irradiation. This is sometimes also called "radiant fluence". | |||
| Spectral exposure | He,ν[nb 3] | joule per square metre per hertz | J⋅m−2⋅Hz−1 | M⋅T−1 | Radiant exposure of a surface per unit frequency or wavelength. The latter is commonly measured in J⋅m−2⋅nm−1. This is sometimes also called "spectral fluence". | |||
| He,λ[nb 4] | joule per square metre, per metre | J/m3 | M⋅L−1⋅T−2 | |||||
| Hemispherical emissivity | ε | N/A | 1 | Radiant exitance of a surface, divided by that of a black body at the same temperature as that surface. | ||||
| Spectral hemispherical emissivity | εν or ελ |
N/A | 1 | Spectral exitance of a surface, divided by that of a black body at the same temperature as that surface. | ||||
| Directional emissivity | εΩ | N/A | 1 | Radiance emitted by a surface, divided by that emitted by a black body at the same temperature as that surface. | ||||
| Spectral directional emissivity | εΩ,ν or εΩ,λ |
N/A | 1 | Spectral radiance emitted by a surface, divided by that of a black body at the same temperature as that surface. | ||||
| Hemispherical absorptance | A | N/A | 1 | Radiant flux absorbed by a surface, divided by that received by that surface. This should not be confused with "absorbance". | ||||
| Spectral hemispherical absorptance | Aν or Aλ |
N/A | 1 | Spectral flux absorbed by a surface, divided by that received by that surface. This should not be confused with "spectral absorbance". | ||||
| Directional absorptance | AΩ | N/A | 1 | Radiance absorbed by a surface, divided by the radiance incident onto that surface. This should not be confused with "absorbance". | ||||
| Spectral directional absorptance | AΩ,ν or AΩ,λ |
N/A | 1 | Spectral radiance absorbed by a surface, divided by the spectral radiance incident onto that surface. This should not be confused with "spectral absorbance". | ||||
| Hemispherical reflectance | R | N/A | 1 | Radiant flux reflected by a surface, divided by that received by that surface. | ||||
| Spectral hemispherical reflectance | Rν or Rλ |
N/A | 1 | Spectral flux reflected by a surface, divided by that received by that surface. | ||||
| Directional reflectance | RΩ | N/A | 1 | Radiance reflected by a surface, divided by that received by that surface. | ||||
| Spectral directional reflectance | RΩ,ν or RΩ,λ |
N/A | 1 | Spectral radiance reflected by a surface, divided by that received by that surface. | ||||
| Hemispherical transmittance | T | N/A | 1 | Radiant flux transmitted by a surface, divided by that received by that surface. | ||||
| Spectral hemispherical transmittance | Tν or Tλ |
N/A | 1 | Spectral flux transmitted by a surface, divided by that received by that surface. | ||||
| Directional transmittance | TΩ | N/A | 1 | Radiance transmitted by a surface, divided by that received by that surface. | ||||
| Spectral directional transmittance | TΩ,ν or TΩ,λ |
N/A | 1 | Spectral radiance transmitted by a surface, divided by that received by that surface. | ||||
| Hemispherical attenuation coefficient | μ | reciprocal metre | m−1 | L−1 | Radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume. | |||
| Spectral hemispherical attenuation coefficient | μν or μλ |
reciprocal metre | m−1 | L−1 | Spectral radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume. | |||
| Directional attenuation coefficient | μΩ | reciprocal metre | m−1 | L−1 | Radiance absorbed and scattered by a volume per unit length, divided by that received by that volume. | |||
| Spectral directional attenuation coefficient | μΩ,ν or μΩ,λ |
reciprocal metre | m−1 | L−1 | Spectral radiance absorbed and scattered by a volume per unit length, divided by that received by that volume. | |||
| See also: SI · Radiometry · Photometry | ||||||||
- ↑ Standards organizations recommend that radiometric quantities should be denoted with suffix "e" (for "energetic") to avoid confusion with photometric or photon quantities.
- ↑ 2.0 2.1 2.2 2.3 2.4 Alternative symbols sometimes seen: W or E for radiant energy, P or F for radiant flux, I for irradiance, W for radiant exitance.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Spectral quantities given per unit frequency are denoted with suffix "ν" (Greek)—not to be confused with suffix "v" (for "visual") indicating a photometric quantity.
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 Spectral quantities given per unit wavelength are denoted with suffix "λ" (Greek).
- ↑ 5.0 5.1 Directional quantities are denoted with suffix "Ω" (Greek).
See also
- Radiosity
References
- ↑ 1.0 1.1 1.2 "Thermal insulation — Heat transfer by radiation — Vocabulary". ISO_9288:2022. International Organization for Standardization. 2022. https://www.iso.org/standard/82088.html. Retrieved 2023-06-17.
 |  |
