International System of Units
The International System of Units, internationally known by the abbreviation SI (from French Système international d'unités), is the modern form of the metric system and the world's most widely used system of measurement. It is the only system of measurement with official status in nearly every country in the world, employed in science, technology, industry, and everyday commerce. The SI system is coordinated by the International Bureau of Weights and Measures, which is abbreviated BIPM from French: Bureau international des poids et mesures.
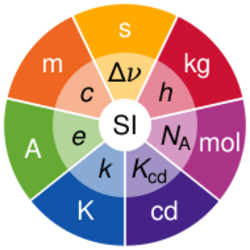
| Symbol | Name | Quantity |
|---|---|---|
| s | second | time |
| m | metre | length |
| kg | kilogram | mass |
| A | ampere | electric current |
| K | kelvin | thermodynamic temperature |
| mol | mole | amount of substance |
| cd | candela | luminous intensity |
The SI comprises a coherent system of units of measurement starting with seven base units, which are the second (symbol s, the unit of time), metre (m, length), kilogram (kg, mass), ampere (A, electric current), kelvin (K, thermodynamic temperature), mole (mol, amount of substance), and candela (cd, luminous intensity). The system can accommodate coherent units for an unlimited number of additional quantities. These are called coherent derived units, which can always be represented as products of powers of the base units. Twenty-two coherent derived units have been provided with special names and symbols.
The seven base units and the 22 coherent derived units with special names and symbols may be used in combination to express other coherent derived units. Since the sizes of coherent units will be convenient for only some applications and not for others, the SI provides twenty-four prefixes which, when added to the name and symbol of a coherent unit produce twenty-four additional (non-coherent) SI units for the same quantity; these non-coherent units are always decimal (i.e. power-of-ten) multiples and sub-multiples of the coherent unit.
The current way of defining the SI is a result of a decades-long move towards increasingly abstract and idealised formulation in which the realisations of the units are separated conceptually from the definitions. A consequence is that as science and technologies develop, new and superior realisations may be introduced without the need to redefine the unit. One problem with artefacts is that they can be lost, damaged, or changed; another is that they introduce uncertainties that cannot be reduced by advancements in science and technology.
The original motivation for the development of the SI was the diversity of units that had sprung up within the centimetre–gram–second (CGS) systems (specifically the inconsistency between the systems of electrostatic units and electromagnetic units) and the lack of coordination between the various disciplines that used them. The General Conference on Weights and Measures (French: Conférence générale des poids et mesures – CGPM), which was established by the Metre Convention of 1875, brought together many international organisations to establish the definitions and standards of a new system and to standardise the rules for writing and presenting measurements. The system was published in 1960 as a result of an initiative that began in 1948, and is based on the metre–kilogram–second system of units (MKS) combined with ideas from the development of the CGS system.
Definition
The International System of Units consists of a set of seven defining constants with seven corresponding base units, derived units, and a set of decimal-based multipliers that are used as prefixes.[1]: 125
SI defining constants
| Symbol | Defining constant | Exact value |
|---|---|---|
| ΔνCs | hyperfine transition frequency of 133Cs | 9192631770 Hz |
| c | speed of light | 299792458 m/s |
| h | Planck constant | 6.62607015×10−34 J⋅s |
| e | elementary charge | 1.602176634×10−19 C |
| k | Boltzmann constant | 1.380649×10−23 J/K |
| NA | Avogadro constant | 6.02214076×1023 mol−1 |
| Kcd | luminous efficacy of 540 THz radiation | 683 lm/W |
The seven defining constants are the most fundamental feature of the definition of the system of units.[1]: 125 The magnitudes of all SI units are defined by declaring that seven constants have certain exact numerical values when expressed in terms of their SI units. These defining constants are the speed of light in vacuum c, the hyperfine transition frequency of caesium ΔνCs, the Planck constant h, the elementary charge e, the Boltzmann constant k, the Avogadro constant NA, and the luminous efficacy Kcd. The nature of the defining constants ranges from fundamental constants of nature such as c to the purely technical constant Kcd. The values assigned to these constants were fixed to ensure continuity with previous definitions of the base units.[1]: 128
SI base units
The SI selects seven units to serve as base units, corresponding to seven base physical quantities. They are the second, with the symbol s, which is the SI unit of the physical quantity of time; the metre, symbol m, the SI unit of length; kilogram (kg, the unit of mass); ampere (A, electric current); kelvin (K, thermodynamic temperature); mole (mol, amount of substance); and candela (cd, luminous intensity).[1] The base units are defined in terms of the defining constants. For example, the kilogram is defined by taking the Planck constant h to be 6.62607015×10−34 J⋅s, giving the expression in terms of the defining constants[1]: 131
- 1 kg = (299792458)2/(6.62607015×10−34)(9192631770)h ΔνCs/c2.
All units in the SI can be expressed in terms of the base units, and the base units serve as a preferred set for expressing or analysing the relationships between units. The choice of which and even how many quantities to use as base quantities is not fundamental or even unique – it is a matter of convention.[1]: 126
| Unit name | Unit symbol | Dimension symbol | Quantity name | Typical symbols | Definition |
|---|---|---|---|---|---|
| second | s | time | The duration of 9192631770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom. | ||
| metre | m | length | , , , etc. | The distance travelled by light in vacuum in 1/299792458 second. | |
| kilogram [n 1] |
kg | mass | The kilogram is defined by setting the Planck constant h to 6.62607015×10−34 J⋅s (J = kg⋅m2⋅s−2), given the definitions of the metre and the second.[2] | ||
| ampere | A | electric current | The flow of 1/1.602176634×10−19 times the elementary charge e per second, which is approximately 6.2415090744×1018 elementary charges per second. | ||
| kelvin | K | thermodynamic temperature |
The kelvin is defined by setting the fixed numerical value of the Boltzmann constant k to 1.380649×10−23 J⋅K−1, (J = kg⋅m2⋅s−2), given the definition of the kilogram, the metre, and the second. | ||
| mole | mol | amount of substance | The amount of substance of 6.02214076×1023 elementary entities.[n 2] This number is the fixed numerical value of the Avogadro constant, NA, when expressed in the unit mol−1. | ||
| candela | cd | luminous intensity | The luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 5.4×1014 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian. | ||
| |||||
Derived units
The system allows for an unlimited number of additional units, called derived units, which can always be represented as products of powers of the base units, possibly with a nontrivial numeric multiplier. When that multiplier is one, the unit is called a coherent derived unit. For example, the coherent derived SI unit of velocity is the metre per second, with the symbol m/s.[1]: 139 The base and coherent derived units of the SI together form a coherent system of units (the set of coherent SI units). A useful property of a coherent system is that when the numerical values of physical quantities are expressed in terms of the units of the system, then the equations between the numerical values have exactly the same form, including numerical factors, as the corresponding equations between the physical quantities.[3]: 6
Twenty-two coherent derived units have been provided with special names and symbols as shown in the table below. The radian and steradian have no base units but are treated as derived units for historical reasons.[1]: 137
| Name | Symbol | Quantity | In SI base units | In other SI units |
|---|---|---|---|---|
| radian[nc 1] | rad | plane angle | 1 | |
| steradian[nc 1] | sr | solid angle | 1 | |
| hertz | Hz | frequency | s−1 | |
| newton | N | force | kg⋅m⋅s−2 | |
| pascal | Pa | pressure, stress | kg⋅m−1⋅s−2 | N/m2 = J/m3 |
| joule | J | energy, work, amount of heat | kg⋅m2⋅s−2 | N⋅m = Pa⋅m3 |
| watt | W | power, radiant flux | kg⋅m2⋅s−3 | J/s |
| coulomb | C | electric charge | s⋅A | |
| volt | V | electric potential difference[lower-alpha 1] | kg⋅m2⋅s−3⋅A−1 | W/A = J/C |
| farad | F | capacitance | kg−1⋅m−2⋅s4⋅A2 | C/V = C2/J |
| ohm | Ω | electrical resistance | kg⋅m2⋅s−3⋅A−2 | V/A = J⋅s/C2 |
| siemens | S | electrical conductance | kg−1⋅m−2⋅s3⋅A2 | Ω−1 |
| weber | Wb | magnetic flux | kg⋅m2⋅s−2⋅A−1 | V⋅s |
| tesla | T | magnetic flux density | kg⋅s−2⋅A−1 | Wb/m2 |
| henry | H | inductance | kg⋅m2⋅s−2⋅A−2 | Wb/A |
| degree Celsius | °C | Celsius temperature | K | |
| lumen | lm | luminous flux | cd⋅sr[nc 2] | cd⋅sr |
| lux | lx | illuminance | cd⋅sr⋅m−2[nc 2] | lm/m2 |
| becquerel | Bq | activity referred to a radionuclide | s−1 | |
| gray | Gy | absorbed dose, kerma | m2⋅s−2 | J/kg |
| sievert | Sv | dose equivalent | m2⋅s−2 | J/kg |
| katal | kat | catalytic activity | mol⋅s−1 | |
| Notes | ||||
The derived units in the SI are formed by powers, products, or quotients of the base units and are unlimited in number.[1]: 138 [4]: 14, 16

Derived units apply to some derived quantities, which may by definition be expressed in terms of base quantities, and thus are not independent; for example, electrical conductance is the inverse of electrical resistance, with the consequence that the siemens is the inverse of the ohm, and similarly, the ohm and siemens can be replaced with a ratio of an ampere and a volt, because those quantities bear a defined relationship to each other.[lower-alpha 2] Other useful derived quantities can be specified in terms of the SI base and derived units that have no named units in the SI, such as acceleration, which has the SI unit m/s2.[1]: 139
A combination of base and derived units may be used to express a derived unit. For example, the SI unit of force is the newton (N), the SI unit of pressure is the pascal (Pa) – and the pascal can be defined as one newton per square metre (N/m2).[5]
Prefixes
Like all metric systems, the SI uses metric prefixes to systematically construct, for the same physical quantity, a set of units that are decimal multiples of each other over a wide range. For example, driving distances are normally given in kilometres (symbol km) rather than in metres. Here the metric prefix 'kilo-' (symbol 'k') stands for a factor of 1000; thus, 1 km = 1000 m.
The SI provides twenty-four metric prefixes that signify decimal powers ranging from 10−30 to 1030, the most recent being adopted in 2022.[1]: 143–144 [6][7][8] Most prefixes correspond to integer powers of 1000; the only ones that do not are those for 10, 1/10, 100, and 1/100. The conversion between different SI units for one and the same physical quantity is always through a power of ten. This is why the SI (and metric systems more generally) are called decimal systems of measurement units.[9]
The grouping formed by a prefix symbol attached to a unit symbol (e.g. 'km', 'cm') constitutes a new inseparable unit symbol. This new symbol can be raised to a positive or negative power. It can also be combined with other unit symbols to form compound unit symbols.[1]: 143 For example, g/cm3 is an SI unit of density, where cm3 is to be interpreted as (cm)3.
Prefixes are added to unit names to produce multiples and submultiples of the original unit. All of these are integer powers of ten, and above a hundred or below a hundredth all are integer powers of a thousand. For example, kilo- denotes a multiple of a thousand and milli- denotes a multiple of a thousandth, so there are one thousand millimetres to the metre and one thousand metres to the kilometre. The prefixes are never combined, so for example a millionth of a metre is a micrometre, not a millimillimetre. Multiples of the kilogram are named as if the gram were the base unit, so a millionth of a kilogram is a milligram, not a microkilogram.[10]: 122 [11]: 14
The BIPM specifies 24 prefixes for the International System of Units (SI):
| Prefix | Base 10 | Decimal | English word | Adoption[nb 1] | |||
|---|---|---|---|---|---|---|---|
| Name | Symbol | Short scale | Long scale | ||||
| yotta | Y | 1024 | 1000000000000000000000000 | septillion | quadrillion | 1991 | |
| zetta | Z | 1021 | 1000000000000000000000 | sextillion | trilliard | 1991 | |
| exa | E | 1018 | 1000000000000000000 | quintillion | trillion | 1975 | |
| peta | P | 1015 | 1000000000000000 | quadrillion | billiard | 1975 | |
| tera | T | 1012 | 1000000000000 | trillion | billion | 1960 | |
| giga | G | 109 | 1000000000 | billion | milliard | 1960 | |
| mega | M | 106 | 1000000 | million | 1873 | ||
| kilo | k | 103 | 1000 | thousand | 1795 | ||
| hecto | h | 102 | 100 | hundred | 1795 | ||
| deca | da | 101 | 10 | ten | 1795 | ||
| 100 | 1 | one | – | ||||
| deci | d | 10−1 | 0.1 | tenth | 1795 | ||
| centi | c | 10−2 | 0.01 | hundredth | 1795 | ||
| milli | m | 10−3 | 0.001 | thousandth | 1795 | ||
| micro | μ | 10−6 | 0.000001 | millionth | 1873 | ||
| nano | n | 10−9 | 0.000000001 | billionth | milliardth | 1960 | |
| pico | p | 10−12 | 0.000000000001 | trillionth | billionth | 1960 | |
| femto | f | 10−15 | 0.000000000000001 | quadrillionth | billiardth | 1964 | |
| atto | a | 10−18 | 0.000000000000000001 | quintillionth | trillionth | 1964 | |
| zepto | z | 10−21 | 0.000000000000000000001 | sextillionth | trilliardth | 1991 | |
| yocto | y | 10−24 | 0.000000000000000000000001 | septillionth | quadrillionth | 1991 | |
| |||||||
Coherent and non-coherent SI units
The base units and the derived units formed as the product of powers of the base units with a numerical factor of one form a coherent system of units. Every physical quantity has exactly one coherent SI unit. For example, 1 m/s = (1 m) / (1 s) is the coherent derived unit for velocity.[1]: 139 With the exception of the kilogram (for which the prefix kilo- is required for a coherent unit), when prefixes are used with the coherent SI units, the resulting units are no longer coherent, because the prefix introduces a numerical factor other than one.[1]: 137 For example, the metre, kilometre, centimetre, nanometre, etc. are all SI units of length, though only the metre is a coherent SI unit. The complete set of SI units consists of both the coherent set and the multiples and sub-multiples of coherent units formed by using the SI prefixes.[1]: 138
The kilogram is the only coherent SI unit whose name and symbol include a prefix. For historical reasons, the names and symbols for multiples and sub-multiples of the unit of mass are formed as if the gram were the base unit. Prefix names and symbols are attached to the unit name gram and the unit symbol g respectively. For example, 10−6 kg is written milligram and mg, not microkilogram and μkg.[1]: 144
Several different quantities may share the same coherent SI unit. For example, the joule per kelvin (symbol J/K) is the coherent SI unit for two distinct quantities: heat capacity and entropy; another example is the ampere, which is the coherent SI unit for both electric current and magnetomotive force. This illustrates why it is important not to use the unit alone to specify the quantity. As the SI Brochure states,[1]: 140 "this applies not only to technical texts, but also, for example, to measuring instruments (i.e. the instrument read-out needs to indicate both the unit and the quantity measured)".
Furthermore, the same coherent SI unit may be a base unit in one context, but a coherent derived unit in another. For example, the ampere is a base unit when it is a unit of electric current, but a coherent derived unit when it is a unit of magnetomotive force.[1]: 140
| Name | Symbol | Derived quantity | Typical symbol |
|---|---|---|---|
| square metre | m2 | area | A |
| cubic metre | m3 | volume | V |
| metre per second | m/s | speed, velocity | v |
| metre per second squared | m/s2 | acceleration | a |
| reciprocal metre | m−1 | wavenumber | σ, ṽ |
| vergence (optics) | V, 1/f | ||
| kilogram per cubic metre | kg/m3 | density | ρ |
| kilogram per square metre | kg/m2 | surface density | ρA |
| cubic metre per kilogram | m3/kg | specific volume | v |
| ampere per square metre | A/m2 | current density | j |
| ampere per metre | A/m | magnetic field strength | H |
| mole per cubic metre | mol/m3 | concentration | c |
| kilogram per cubic metre | kg/m3 | mass concentration | ρ, γ |
| candela per square metre | cd/m2 | luminance | Lv |
| Name | Symbol | Quantity | In SI base units |
|---|---|---|---|
| pascal-second | Pa⋅s | dynamic viscosity | m−1⋅kg⋅s−1 |
| newton-metre | N⋅m | moment of force | m2⋅kg⋅s−2 |
| newton per metre | N/m | surface tension | kg⋅s−2 |
| radian per second | rad/s | angular velocity, angular frequency | s−1 |
| radian per second squared | rad/s2 | angular acceleration | s−2 |
| watt per square metre | W/m2 | heat flux density, irradiance | kg⋅s−3 |
| joule per kelvin | J/K | entropy, heat capacity | m2⋅kg⋅s−2⋅K−1 |
| joule per kilogram-kelvin | J/(kg⋅K) | specific heat capacity, specific entropy | m2⋅s−2⋅K−1 |
| joule per kilogram | J/kg | specific energy | m2⋅s−2 |
| watt per metre-kelvin | W/(m⋅K) | thermal conductivity | m⋅kg⋅s−3⋅K−1 |
| joule per cubic metre | J/m3 | energy density | m−1⋅kg⋅s−2 |
| volt per metre | V/m | electric field strength | m⋅kg⋅s−3⋅A−1 |
| coulomb per cubic metre | C/m3 | electric charge density | m−3⋅s⋅A |
| coulomb per square metre | C/m2 | surface charge density, electric flux density, electric displacement | m−2⋅s⋅A |
| farad per metre | F/m | permittivity | m−3⋅kg−1⋅s4⋅A2 |
| henry per metre | H/m | permeability | m⋅kg⋅s−2⋅A−2 |
| joule per mole | J/mol | molar energy | m2⋅kg⋅s−2⋅mol−1 |
| joule per mole-kelvin | J/(mol⋅K) | molar entropy, molar heat capacity | m2⋅kg⋅s−2⋅K−1⋅mol−1 |
| coulomb per kilogram | C/kg | exposure (x- and γ-rays) | kg−1⋅s⋅A |
| gray per second | Gy/s | absorbed dose rate | m2⋅s−3 |
| watt per steradian | W/sr | radiant intensity | m2⋅kg⋅s−3 |
| watt per square metre-steradian | W/(m2⋅sr) | radiance | kg⋅s−3 |
| katal per cubic metre | kat/m3 | catalytic activity concentration | m−3⋅s−1⋅mol |
Lexicographic conventions

Unit names
According to the SI Brochure,[1]: 148 unit names should be treated as common nouns of the context language. This means that they should be typeset in the same character set as other common nouns (e.g. Latin alphabet in English, Cyrillic script in Russian, etc.), following the usual grammatical and orthographical rules of the context language. For example, in English and French, even when the unit is named after a person and its symbol begins with a capital letter, the unit name in running text should start with a lowercase letter (e.g., newton, hertz, pascal) and is capitalised only at the beginning of a sentence and in headings and publication titles. As a nontrivial application of this rule, the SI Brochure notes[1]: 148 that the name of the unit with the symbol °C is correctly spelled as 'degree Celsius': the first letter of the name of the unit, 'd', is in lowercase, while the modifier 'Celsius' is capitalised because it is a proper name.[1]: 148
The English spelling and even names for certain SI units, prefixes and non-SI units depend on the variety of English used. US English uses the spelling deka-, meter, and liter, and International English uses deca-, metre, and litre. The name of the unit whose symbol is t and which is defined by 1 t = 103 kg is 'metric ton' in US English and 'tonne' in International English.[4]: iii
Unit symbols and the values of quantities
Symbols of SI units are intended to be unique and universal, independent of the context language.[10]: 130–135 The SI Brochure has specific rules for writing them.[10]: 130–135
In addition, the SI Brochure provides style conventions for among other aspects of displaying quantities units: the quantity symbols, formatting of numbers and the decimal marker, expressing measurement uncertainty, multiplication and division of quantity symbols, and the use of pure numbers and various angles.[1]: 147
In the United States, the guideline produced by the National Institute of Standards and Technology (NIST)[11]: 37 clarifies language-specific details for American English that were left unclear by the SI Brochure, but is otherwise identical to the SI Brochure.[12] For example, since 1979, the litre may exceptionally be written using either an uppercase "L" or a lowercase "l", a decision prompted by the similarity of the lowercase letter "l" to the numeral "1", especially with certain typefaces or English-style handwriting. NIST recommends that within the United States, "L" be used rather than "l".[11]
Realisation of units

Metrologists carefully distinguish between the definition of a unit and its realisation. The SI units are defined by declaring that seven defining constants[1]: 125–129 have certain exact numerical values when expressed in terms of their SI units. The realisation of the definition of a unit is the procedure by which the definition may be used to establish the value and associated uncertainty of a quantity of the same kind as the unit.[1]: 135
For each base unit the BIPM publishes a mises en pratique, (French for 'putting into practice; implementation',[14]) describing the current best practical realisations of the unit.[15] The separation of the defining constants from the definitions of units means that improved measurements can be developed leading to changes in the mises en pratique as science and technology develop, without having to revise the definitions.
The published mise en pratique is not the only way in which a base unit can be determined: the SI Brochure states that "any method consistent with the laws of physics could be used to realise any SI unit".[10]: 111 Various consultative committees of the CIPM decided in 2016 that more than one mise en pratique would be developed for determining the value of each unit.[16] These methods include the following:
- At least three separate experiments be carried out yielding values having a relative standard uncertainty in the determination of the kilogram of no more than 5×10−8 and at least one of these values should be better than 2×10−8. Both the Kibble balance and the Avogadro project should be included in the experiments and any differences between these be reconciled.[17][18]
- The definition of the kelvin measured with a relative uncertainty of the Boltzmann constant derived from two fundamentally different methods such as acoustic gas thermometry and dielectric constant gas thermometry be better than one part in 10−6 and that these values be corroborated by other measurements.[19]
Organisational status

The International System of Units, or SI,[1]: 123 is a decimal and metric system of units established in 1960 and periodically updated since then. The SI has an official status in most countries, including the United States, Canada, and the United Kingdom, although these three countries are among the handful of nations that, to various degrees, also continue to use their customary systems. Nevertheless, with this nearly universal level of acceptance, the SI "has been used around the world as the preferred system of units, the basic language for science, technology, industry, and trade."[1]: 123, 126
The only other types of measurement system that still have widespread use across the world are the imperial and US customary measurement systems. The international yard and pound are defined in terms of the SI.[20]
International System of Quantities
The quantities and equations that provide the context in which the SI units are defined are now referred to as the International System of Quantities (ISQ). The ISQ is based on the base quantities underlying each of the seven base units of the SI. Derived quantities, such as area, pressure, and electrical resistance, follow from these base quantities by clear, non-contradictory equations. The ISQ defines the quantities that are measured with the SI units.[21] The ISQ is formalised, in part, in the international standard ISO/IEC 80000, which was completed in 2009 with the publication of ISO 80000-1,[22] and has largely been revised in 2019–2020.[23]
Controlling authority
The SI is regulated and continually developed by three international organisations that were established in 1875 under the terms of the Metre Convention. They are the General Conference on Weights and Measures (CGPM[lower-alpha 3]),[24] the International Committee for Weights and Measures (CIPM[lower-alpha 4]), and the International Bureau of Weights and Measures (BIPM[lower-alpha 5]). All the decisions and recommendations concerning units are collected in a brochure called The International System of Units (SI),[1] which is published in French and English by the BIPM and periodically updated. The writing and maintenance of the brochure is carried out by one of the committees of the CIPM. The definitions of the terms "quantity", "unit", "dimension", etc. that are used in the SI Brochure are those given in the international vocabulary of metrology.[25] The brochure leaves some scope for local variations, particularly regarding unit names and terms in different languages. For example, the United States' National Institute of Standards and Technology (NIST) has produced a version of the CGPM document (NIST SP 330), which clarifies usage for English-language publications that use American English.[4]
History

CGS and MKS systems

The concept of a system of units emerged a hundred years before the SI. In the 1860s, James Clerk Maxwell, William Thomson (later Lord Kelvin), and others working under the auspices of the British Association for the Advancement of Science, building on previous work of Carl Gauss, developed the centimetre–gram–second system of units or cgs system in 1874. The systems formalised the concept of a collection of related units called a coherent system of units. In a coherent system, base units combine to define derived units without extra factors.[4]: 2 For example, using metre per second is coherent in a system that uses metre for length and second for time, but kilometre per hour is not coherent. The principle of coherence was successfully used to define a number of units of measure based on the CGS, including the erg for energy, the dyne for force, the barye for pressure, the poise for dynamic viscosity and the stokes for kinematic viscosity.[27]
Metre Convention
A French-inspired initiative for international cooperation in metrology led to the signing in 1875 of the Metre Convention, also called Treaty of the Metre, by 17 nations.[lower-alpha 6][28]: 353–354 The General Conference on Weights and Measures (French: Conférence générale des poids et mesures – CGPM), which was established by the Metre Convention,[27] brought together many international organisations to establish the definitions and standards of a new system and to standardise the rules for writing and presenting measurements.[29]: 37 [30] Initially the convention only covered standards for the metre and the kilogram. This became the foundation of the MKS system of units.[4]: 2
Giovanni Giorgi and the problem of electrical units
At the close of the 19th century three different systems of units of measure existed for electrical measurements: a CGS-based system for electrostatic units, also known as the Gaussian or ESU system, a CGS-based system for electromechanical units (EMU), and an International system based on units defined by the Metre Convention[31] for electrical distribution systems. Attempts to resolve the electrical units in terms of length, mass, and time using dimensional analysis was beset with difficulties – the dimensions depended on whether one used the ESU or EMU systems.[32] This anomaly was resolved in 1901 when Giovanni Giorgi published a paper in which he advocated using a fourth base unit alongside the existing three base units. The fourth unit could be chosen to be electric current, voltage, or electrical resistance.[33]
Electric current with named unit 'ampere' was chosen as the base unit, and the other electrical quantities derived from it according to the laws of physics. When combined with the MKS the new system, known as MKSA, was approved in 1946.[4]
9th CGPM, the precursor to SI
In 1948, the 9th CGPM commissioned a study to assess the measurement needs of the scientific, technical, and educational communities and "to make recommendations for a single practical system of units of measurement, suitable for adoption by all countries adhering to the Metre Convention".[34] This working document was Practical system of units of measurement. Based on this study, the 10th CGPM in 1954 defined an international system derived from six base units: the metre, kilogram, second, ampere, degree Kelvin, and candela.[35]
The 9th CGPM also approved the first formal recommendation for the writing of symbols in the metric system when the basis of the rules as they are now known was laid down.[36] These rules were subsequently extended and now cover unit symbols and names, prefix symbols and names, how quantity symbols should be written and used, and how the values of quantities should be expressed.[10]: 104, 130
Birth of the SI
The 10th CGPM in 1954 resolved to create an international system of units[29]: 41 and in 1960, the 11th CGPM adopted the International System of Units, abbreviated SI from the French name Le Système international d'unités, which included a specification for units of measurement.[10]: 110
The International Bureau of Weights and Measures (BIPM) has described SI as "the modern form of metric system".[10]: 95 In 1968, the unit "degree Kelvin" was renamed "kelvin". In 1971 the mole became the seventh base unit of the SI.[4]: 2
2019 redefinition
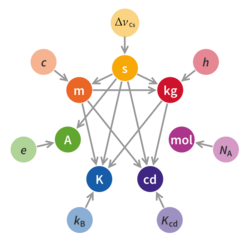
After the metre was redefined in 1960, the International Prototype of the Kilogram (IPK) was the only physical artefact upon which base units (directly the kilogram and indirectly the ampere, mole and candela) depended for their definition, making these units subject to periodic comparisons of national standard kilograms with the IPK.[37] During the 2nd and 3rd Periodic Verification of National Prototypes of the Kilogram, a significant divergence had occurred between the mass of the IPK and all of its official copies stored around the world: the copies had all noticeably increased in mass with respect to the IPK. During extraordinary verifications carried out in 2014 preparatory to redefinition of metric standards, continuing divergence was not confirmed. Nonetheless, the residual and irreducible instability of a physical IPK undermined the reliability of the entire metric system to precision measurement from small (atomic) to large (astrophysical) scales.[38] By avoiding the use of an artefact to define units, all issues with the loss, damage, and change of the artefact are avoided.[1]: 125
A proposal was made that:[39]
- In addition to the speed of light, four constants of nature – the Planck constant, an elementary charge, the Boltzmann constant, and the Avogadro constant – be defined to have exact values
- The International Prototype of the Kilogram be retired
- The current definitions of the kilogram, ampere, kelvin, and mole be revised
- The wording of base unit definitions should change emphasis from explicit unit to explicit constant definitions.
The new definitions were adopted at the 26th CGPM on 16 November 2018, and came into effect on 20 May 2019.[40] The change was adopted by the European Union through Directive (EU) 2019/1258.[41]
Prior to its redefinition in 2019, the SI was defined through the seven base units from which the derived units were constructed as products of powers of the base units. After the redefinition, the SI is defined by fixing the numerical values of seven defining constants. This has the effect that the distinction between the base units and derived units is, in principle, not needed, since all units, base as well as derived, may be constructed directly from the defining constants. Nevertheless, the distinction is retained because "it is useful and historically well established", and also because the ISO/IEC 80000 series of standards, which define the International System of Quantities (ISQ), specifies base and derived quantities that necessarily have the corresponding SI units.[1]: 129
Related units
Non-SI units accepted for use with SI

Many non-SI units continue to be used in the scientific, technical, and commercial literature. Some units are deeply embedded in history and culture, and their use has not been entirely replaced by their SI alternatives. The CIPM recognised and acknowledged such traditions by compiling a list of non-SI units accepted for use with SI,[10] including the hour, minute, degree of angle, litre, and decibel.
This is a list of units that are not defined as part of the International System of Units (SI) but are otherwise mentioned in the SI Brochure,[42] listed as being accepted for use alongside SI units, or for explanatory purposes.
| Name | Symbol | Quantity | Value in SI units |
|---|---|---|---|
| minute | min | time | 1 min = 60 s |
| hour | h | 1 h = 60 min = 3600 s | |
| day | d | 1 d = 24 h = 1440 min = 86400 s | |
| astronomical unit | au | length | 1 au = 149597870700 m |
| degree | ° | plane angle and phase angle | 1° = (π / 180) rad |
| arcminute | ′ | 1′ = (1 / 60)° = (π / 10800) rad | |
| arcsecond | ″ | 1″ = (1 / 60)′ = (1 / 3600)° = (π / 648000) rad | |
| hectare | ha | area | 1 ha = 1 hm2 = 10000 m2 |
| litre | l, L | volume | 1 L = 1 dm3 = 1000 cm3 = 0.001 m3 |
| tonne | t | mass | 1 t = 1 Mg = 1000 kg |
| dalton | Da | 1 Da = 1.66053906660(50)×10−27 kg[43][lower-alpha 7] | |
| electronvolt | eV | energy | 1 eV = 1.602176634×10−19 J[44] |
| neper | Np | logarithmic ratio quantity | N/A |
| bel, decibel | B, dB | N/A |
The SI prefixes can be used with several of these units, but not, for example, with the non-SI units of time. Others, in order to be converted to the corresponding SI unit, require conversion factors that are not powers of ten. Some common examples of such units are the customary units of time, namely the minute (conversion factor of 60 s/min, since 1 min = 60 s), the hour (3600 s), and the day (86400 s); the degree (for measuring plane angles, 1° = (π /180) rad); and the electronvolt (a unit of energy, 1 eV = 1.602176634×10−19 J).[42]
Metric units not recognised by SI
Although the term metric system is often used as an informal alternative name for the International System of Units,[45] other metric systems exist, some of which were in widespread use in the past or are even still used in particular areas. There are also individual metric units such as the sverdrup and the darcy that exist outside of any system of units. Most of the units of the other metric systems are not recognised by the SI.
Unacceptable uses
Sometimes, SI unit name variations are introduced, mixing information about the corresponding physical quantity or the conditions of its measurement; however, this practice is unacceptable with the SI. "Unacceptability of mixing information with units: When one gives the value of a quantity, any information concerning the quantity or its conditions of measurement must be presented in such a way as not to be associated with the unit."[10] Instances include: "watt-peak" and "watt RMS"; "geopotential metre" and "vertical metre"; "standard cubic metre"; "atomic second", "ephemeris second", and "sidereal second".
See also
- Conversion of units – Comparison of various scales
- Biology:List of international common standards
- Outline of the metric system – Overview of and topical guide to the metric system
Organisations
- Organization:International Bureau of Weights and Measures
- Organization:Institute for Reference Materials and Measurements
- National Institute of Standards and Technology
Standards and conventions
- Physics:Conventional electrical unit – Unit of measurement in the field of electricity
- Physics:Coordinated Universal Time (UTC) – Primary time standard
- Unified Code for Units of Measure – System of codes for unambiguously representing measurement units
Notes
- ↑ Electric potential difference is also called "voltage" in many countries, as well as "electric tension" or simply "tension" in some countries.
- ↑ Ohm's law: 1 Ω = 1 V/A from the relationship E = I × R, where E is electromotive force or voltage (unit: volt), I is current (unit: ampere), and R is resistance (unit: ohm).
- ↑ From French: Conférence générale des poids et mesures.
- ↑ from French: Comité international des poids et mesures
- ↑ from French: Bureau international des poids et mesures
- ↑ Argentina, Austria-Hungary, Belgium, Brazil, Denmark, France, German Empire, Italy, Peru, Portugal, Russia, Spain, Sweden and Norway, Switzerland, Ottoman Empire, United States, and Venezuela.
- ↑ A footnote in the 9th SI Brochure gives an exact definition of the dalton.
- Attribution
[1]![]() This article incorporates text from this source, which is available under the CC BY 3.0 license.
This article incorporates text from this source, which is available under the CC BY 3.0 license.
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 1.15 1.16 1.17 1.18 1.19 1.20 1.21 1.22 1.23 1.24 1.25 1.26 1.27 1.28 1.29 1.30 1.31 International Bureau of Weights and Measures (Dec 2022), The International System of Units (SI), 2 (9th ed.), ISBN 978-92-822-2272-0, https://www.bipm.org/documents/20126/41483022/SI-Brochure-9-EN.pdf
- ↑ Materese, Robin (16 November 2018). "Historic Vote Ties Kilogram and Other Units to Natural Constants". NIST. https://www.nist.gov/news-events/news/2018/11/historic-vote-ties-kilogram-and-other-units-natural-constants.
- ↑ ISO 80000-1:2009 Quantities and units – Part 1: General, https://www.iso.org/standard/30669.html
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 The International System of Units (SI) (NIST Special publication 330, 2019 ed.). Gaithersburg, MD: NIST. 2019. https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.330-2019.pdf. Retrieved 30 November 2019.
- ↑ "Units & Symbols for Electrical & Electronic Engineers". Institution of Engineering and Technology. 1996. pp. 8–11. http://www.theiet.org/students/resources/units-symbols.cfm.
- ↑ Lawler, Daniel (18 November 2022). "Earth now weighs six ronnagrams: New metric prefixes voted in". phys.org. https://phys.org/news/2022-11-earth-ronnagrams-metric-prefixes-voted.html.
- ↑ "List of Resolutions for the 27th meeting of the General Conference on Weights and Measures". BIPM. 18 November 2022. https://www.bipm.org/documents/20126/64811223/Resolutions-2022.pdf.
- ↑ "New prefixes for the SI adopted by the General Conference on Weights and Measures". https://www.bipm.org/en/-/2022-12-19-si-prefixes.
- ↑ "Decimal Nature of the Metric System". US Metric Association. 2015. https://usma.org/decimal-nature-of-the-metric-system.
- ↑ 10.0 10.1 10.2 10.3 10.4 10.5 10.6 10.7 10.8 International Bureau of Weights and Measures (2006), The International System of Units (SI) (8th ed.), ISBN 92-822-2213-6, http://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf
- ↑ 11.0 11.1 11.2 Thompson, Ambler; Taylor, Barry N. (March 2008). Guide for the Use of the International System of Units (SI) (Report). National Institute of Standards and Technology. §10.5.3. https://www.nist.gov/pml/special-publication-811. Retrieved 21 January 2022.
- ↑ "Interpretation of the International System of Units (the Metric System of Measurement) for the United States". Federal Register 73 (96): 28432–28433. 9 May 2008. FR Doc number E8-11058. http://edocket.access.gpo.gov/2008/pdf/E8-11058.pdf. Retrieved 28 October 2009.
- ↑ "Avogadro Project". National Physical Laboratory. http://www.npl.co.uk/science-technology/mass-and-force/research/avogadro-project.
- ↑ "NIST Mise en Pratique of the New Kilogram Definition". NIST. 2013. https://www.nist.gov/programs-projects/nist-mise-en-pratique-new-kilogram-definition. Retrieved 9 May 2020.
- ↑ "Practical realizations of the definitions of some important units". BIPM. 2019. https://www.bipm.org/en/publications/mises-en-pratique/.
- ↑ "International Committee for Weights and Measures – Proceedings of the 106th meeting". https://www.bipm.org/utils/en/pdf/CIPM/CIPM2017-EN.pdf.
- ↑ "Recommendations of the Consultative Committee for Mass and Related Quantities to the International Committee for Weights and Measures". Sèvres: Bureau International des Poids et Mesures. 26 March 2010. http://www.bipm.org/utils/common/pdf/CCM12.pdf#page=23.
- ↑ "Recommendations of the Consultative Committee for Amount of Substance – Metrology in Chemistry to the International Committee for Weights and Measures". Sèvres: Bureau International des Poids et Mesures. 15–16 April 2010. http://www.bipm.org/utils/common/pdf/CCQM16.pdf#page=40.
- ↑ "Recommendations of the Consultative Committee for Thermometry to the International Committee for Weights and Measures". Sèvres: Bureau International des Poids et Mesures. 6–7 May 2010. http://www.bipm.org/utils/common/pdf/CCT25.pdf#page=53.
- ↑ United States. National Bureau of Standards (1959). Research Highlights of the National Bureau of Standards. U.S. Department of Commerce, National Bureau of Standards. p. 13. https://books.google.com/books?id=4aWN-VRV1AoC&pg=PA13. Retrieved 31 July 2019.
- ↑ "1.16". International vocabulary of metrology – Basic and general concepts and associated terms (VIM) (3rd ed.). International Bureau of Weights and Measures (BIPM): Joint Committee for Guides in Metrology. 2012. http://www.bipm.org/utils/common/documents/jcgm/JCGM_200_2012.pdf. Retrieved 28 March 2015.
- ↑ S. V. Gupta, Units of Measurement: Past, Present and Future. International System of Units, p. 16, Springer, 2009. ISBN 3642007384.
- ↑ "ISO 80000-1:2022 Quantities and units Part 1: General". https://www.iso.org/standard/76921.html.
- ↑ "Interpretation of the International System of Units (the Metric System of Measurement) for the United States". Federal Register (National Institute of Standards and Technology) 73: 28432. 16 May 2008. https://www.federalregister.gov/documents/2008/05/16/E8-11058/interpretation-of-the-international-system-of-units-the-metric-system-of-measurement-for-the-united. Retrieved 6 December 2022.
- ↑ "VIM3: International Vocabulary of Metrology". http://www.bipm.org/en/publications/guides/vim.html.
- ↑ "Amtliche Maßeinheiten in Europa 1842" (in de). 1 May 2009. http://www.spasslernen.de/geschichte/groessen/mas1.htm. Text version of Malaisé's book: (in de) Theoretisch-practischer Unterricht im Rechnen. München: Verlag des Verf.. 1842. pp. 307–322. https://archive.org/details/bub_gb_TQgHAAAAcAAJ. Retrieved 7 January 2013.
- ↑ 27.0 27.1 The International Bureau of Weights and Measures 1875–1975: NBS Special Publication 420. Washington, D.C.: National Bureau of Standards. 20 May 1975. p. 12. https://archive.org/details/internationalbur420page.
- ↑ The Measure of all Things – The Seven-Year-Odyssey that Transformed the World. London: Abacus. 2002. ISBN 978-0-349-11507-8.
- ↑ 29.0 29.1 Giunta, Carmen J. (2023) (in en). A Brief History of the Metric System: From Revolutionary France to the Constant-Based SI. SpringerBriefs in Molecular Science. Cham: Springer International Publishing. doi:10.1007/978-3-031-28436-6. ISBN 978-3-031-28435-9. Bibcode: 2023bhms.book.....G. https://link.springer.com/10.1007/978-3-031-28436-6.
- ↑ Quinn, Terry J. (2012). From artefacts to atoms: the BIPM and the search for ultimate measurement standards. New York Oxford: Oxford University Press. ISBN 978-0-19-530786-3.
- ↑ Weights, Measures and Units. Oxford University Press. 2002. International unit. ISBN 978-0-19-860522-5. https://archive.org/details/dictionaryofweig0000fenn.
- ↑ A treatise on electricity and magnetism. 2. Oxford: Clarendon Press. 1873. pp. 242–245. https://archive.org/stream/electricandmag02maxwrich. Retrieved 12 May 2011.
- ↑ "In the beginning...: Giovanni Giorgi". International Electrotechnical Commission. http://www.iec.ch/about/history/beginning/giovanni_giorgi.htm.
- ↑ "Resolution 6 of the 9th CGPM". 1948. http://www.bipm.org/en/CGPM/db/9/6/.
- ↑ International Bureau of Weights and Measures (2019-05-20), SI Brochure: The International System of Units (SI) (9th ed.), p. 163, ISBN 978-92-822-2272-0, https://www.bipm.org/utils/common/pdf/si-brochure/SI-Brochure-9.pdf
- ↑ "Resolution 7 of the 9th meeting of the CGPM (1948): Writing and printing of unit symbols and of numbers". International Bureau of Weights and Measures. 1948. http://www.bipm.org/en/CGPM/db/9/7/.
- ↑ "Redefining the kilogram". UK National Physical Laboratory. http://www.npl.co.uk/educate-explore/redefining-the-kilogram/.
- ↑ "A Turning Point for Humanity: Redefining the World's Measurement System" (in en). 12 May 2018. https://www.nist.gov/si-redefinition/turning-point-humanity-redefining-worlds-measurement-system.
- ↑ "Appendix 1. Decisions of the CGPM and the CIPM". BIPM. p. 188. https://www.bipm.org/documents/20126/41483022/SI-Brochure-9-App4-EN.pdf.
- ↑ "Report on the Meeting of the CODATA Task Group on Fundamental Constants". BIPM. 3–4 November 2014. p. 7. http://www.bipm.org/cc/TGFC/Allowed/Minutes/CODATA_Minutes_14-BIPM-public.pdf. "[BIPM director Martin] Milton responded to a question about what would happen if ... the CIPM or the CGPM voted not to move forward with the redefinition of the SI. He responded that he felt that by that time the decision to move forward should be seen as a foregone conclusion."
- ↑ "Commission Directive (EU) 2019/1258 of 23 July 2019 amending, for the purpose of its adaptation to technical progress, the Annex to Council Directive 80/181/EEC as regards the definitions of SI base units". 23 July 2019. https://eur-lex.europa.eu/eli/dir/2019/1258/oj.
- ↑ 42.0 42.1 Bureau international des poids et mesures, "Non-SI units that are accepted for use with the SI", in: Le Système international d'unités (SI) / The International System of Units (SI), 9th ed. (Sèvres: 2019), ISBN 9789282222720, c. 4, pp. 145–146.
- ↑ "2018 CODATA Value: atomic mass constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. http://physics.nist.gov/cgi-bin/cuu/Value?u. Retrieved 2019-05-20.
- ↑ "2018 CODATA Value: electron volt". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. http://physics.nist.gov/cgi-bin/cuu/Value?evj. Retrieved 2019-05-20.
- ↑ Olthoff, Jim (2018). "For All Times, For All Peoples: How Replacing the Kilogram Empowers Industry". NIST. https://www.nist.gov/blogs/taking-measure/all-times-all-peoples-how-replacing-kilogram-empowers-industry. Retrieved 14 April 2020. "... the International System of Units (SI), popularly known as the metric system.".
Further reading
- International Union of Pure and Applied Chemistry (1993). Quantities, Units and Symbols in Physical Chemistry, 2nd edition, Oxford: Blackwell Science. ISBN 0-632-03583-8. Electronic version.
- Unit Systems in Electromagnetism
- MW Keller et al. (PDF) Metrology Triangle Using a Watt Balance, a Calculable Capacitor, and a Single-Electron Tunnelling Device
- "The Current SI Seen From the Perspective of the Proposed New SI" (PDF). Barry N. Taylor. Journal of Research of the National Institute of Standards and Technology, Vol. 116, No. 6, Pgs. 797–807, Nov–Dec 2011.
- B. N. Taylor, Ambler Thompson, International System of Units (SI), National Institute of Standards and Technology 2008 edition, ISBN 1437915582.
External links
 |

