Physics:Movable cellular automaton

Short description: Method in computational solid mechanics based on the discrete concept

Movable cellular automaton method

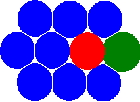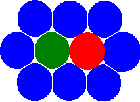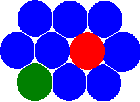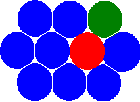
Animation of a movable cellular automaton being used to simulate friction at the interface between two surfaces
Method type
Continuous/Discrete	Discrete
Analytical/Computational	Computational
Characteristics
Influenced by	cellular automaton, discrete element
Method in	computational solid mechanics

The movable cellular automaton (MCA) method is a method in computational solid mechanics based on the discrete concept. It provides advantages both of classical cellular automaton and discrete element methods. One important advantage of the MCA method is that it permits direct simulation of material fracture, including damage generation, crack propagation, fragmentation, and mass mixing. It is difficult to simulate these processes by means of continuum mechanics methods (For example: finite element method, finite difference method, etc.), so some new concepts like peridynamics are required. Discrete element method is very effective to simulate granular materials, but mutual forces among movable cellular automata provides simulating solids behavior. As the cell size of the automaton approaches zero, MCA behavior approaches classical continuum mechanics methods. The MCA method was developed in the group of S.G. Psakhie

Keystone of the movable cellular automaton method

Object (at left) is described as set of interacted automata (at center). At right is shown velocity field of automata.

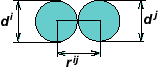
In framework of the MCA approach an object under modeling is considered as a set of interacting elements/automata. The dynamics of the set of automata are defined by their mutual forces and rules for their relationships. This system exists and operates in time and space. Its evolution in time and space is governed by the equations of motion. The mutual forces and rules for inter-elements relationships are defined by the function of the automaton response. This function has to be specified for each automaton. Due to mobility of automata the following new parameters of cellular automata have to be included into consideration: Rⁱ – radius-vector of automaton; Vⁱ – velocity of automaton; ωⁱ – rotation velocity of automaton; θⁱ – rotation vector of automaton; mⁱ – mass of automaton; Jⁱ – moment of inertia of automaton.

New concept: neighbours

Each automaton has some neighbors

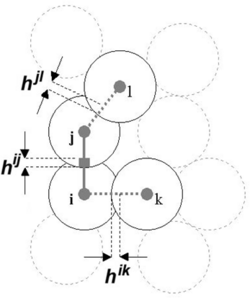
The new concept of the MCA method is based on the introducing of the state of the pair of automata (relation of interacting pairs of automata) in addition to the conventional one – the state of a separate automaton. Note that the introduction of this definition allows to go from the static net concept to the concept of neighbours. As a result of this, the automata have the ability to change their neighbors by switching the states (relationships) of the pairs.

Definition of the parameter of pair state

The introducing of new type of states leads to new parameter to use it as criteria for switching relationships. It is defined as an automaton overlapping parameters h^ij. So the relationship of the cellular automata is characterised by the value of their overlapping.

The initial structure is formed by setting up certain relationships among each pair of neighboring elements.

Criterion of switching of the state of pair relationships

At left pair of automata ij is linked. At right pair of automata ij is unlinked.

In contrast to the classical cellular automaton method in the MCA method not only a single automaton but also a relationship of pair of automata can be switched. According with the bistable automata concept there are two types of the pair states (relationships):

linked	– both automata belong to a solid
unlinked	– each automaton of the pair belongs to different bodies or parts of damaged body.

So the changing of the state of pair relationships is controlled by relative movements of the automata and the media formed by such pairs can be considered as bistable media.

Equations of MCA motion

The evolution of MCA media is described by the following equations of motion for translation:

[math]\displaystyle{ {d^2 h^{ij} \over dt^2} = \left( {1 \over m^i} + {1 \over m^j} \right) p^{ij} + \sum_{k\neq j} C(ij,ik) \psi(\alpha_{ij,ik}) {1 \over m^i} p^{ik} + \sum_{l \neq i} C(ij,jl) \psi(\alpha_{ij,jl}) {1 \over m^j} p^{jl} }[/math]

Forces between automata ij coming from their neighbors.

Here [math]\displaystyle{ m^i }[/math] is the mass of automaton [math]\displaystyle{ i }[/math], [math]\displaystyle{ p^{ij} }[/math] is central force acting between automata [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math], [math]\displaystyle{ C(ij,ik) }[/math] is certain coefficient associated with transferring the h parameter from pair ij to pair ik, [math]\displaystyle{ \psi(\alpha_{ij,ik}) }[/math] is the angle between directions ij and ik.

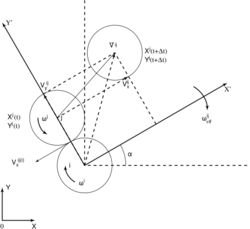
Due to finite size of movable automata the rotation effects have to be taken into account. The equations of motion for rotation can be written as follows:

[math]\displaystyle{ {d^2 \theta^{ij} \over dt^2} = \left( {q^{ij} \over J^i} + {q^{ji} \over J^j} \right) \tau^{ij} + \sum_{k\neq j} S(ij,ik) {q^{ik} \over J^i} \tau^{ik} + \sum_{l\neq j} S(ij,jl) {q^{jl} \over J^j} \tau^{jl} }[/math]

Here Θ^ij is the angle of relative rotation (it is a switching parameter like h^ij for translation), q^ij is the distance from center of automaton i to contact point of automaton j (moment arm), τ^ij is the pair tangential interaction, [math]\displaystyle{ S(ij,ik) }[/math] is certain coefficient associated with transferring the Θ parameter from one pair to other (it is similar to [math]\displaystyle{ C(ij,ik) }[/math] from the equation for translation).

These equations are completely similar to the equations of motion for the many–particle approach.

Definition of deformation in pair of automata

Rotation of body as whole not caused to deformation in pair of automata

Translation of the pair automata The dimensionless deformation parameter for translation of the i j automata pair can be presented as:

[math]\displaystyle{ \varepsilon^{ij} = {h^{ij} \over r_{0}^{ij}} = { \left( q^{ij} + q^{ji} \right) - \left( d^{i} + d^{j} \right) \big / 2 \over \left( d^{i} + d^{j} \right) \big / 2 } }[/math]

In this case:

[math]\displaystyle{ \left( \Delta{\varepsilon^{i(j)}} + \Delta{\varepsilon^{j(i)}} \right) { \left( d^{i} + d^{j} \right) \over 2} = V_{n}^{ij} \Delta{t} }[/math]

where Δt time step, V_n^ij – relative velocity.

Rotation of the pair automata can be calculated by analogy with the last translation relationships.

Modeling of irreversible deformation in the MCA method

Deformation is determine by value of distance from the center of automaton

There are two types of the response function of automata

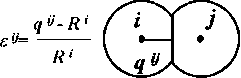
The ε^ij parameter is used as a measure of deformation of automaton i under its interaction with automaton j. Where q^ij – is a distance from the center of automaton i to its contact point with automaton j; Rⁱ = dⁱ/2 (dⁱ – is the size of automaton i).

As an example the titanium specimen under cyclic loading (tension – compression) is considered. The loading diagram is shown in the next figure:

Scheme of loading	Loading diagram
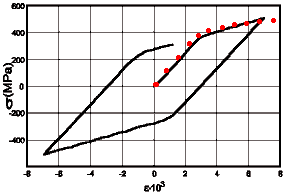
	(Red marks are the experimental data)

Advantages of MCA method

Due to mobility of each automaton the MCA method allows to take into account directly such actions as:

• mass mixing
• penetration effects
• chemical reactions
• intensive deformation
• phase transformations
• accumulation of damages
• fragmentation and fracture
• cracks generation and development

Using boundary conditions of different types (fixed, elastic, viscous-elastic, etc.) it is possible to imitate different properties of surrounding medium, containing the simulated system. It is possible to model different modes of mechanical loading (tension, compression, shear strain, etc.) by setting up additional conditions at the boundaries.

See also

• Physics:Continuum mechanics – Branch of physics which studies the behavior of materials modeled as continuous media
• Physics:Solid mechanics – Branch of mechanics concerned with solid materials and their behaviors
• Fracture mechanics – Study of propagation of cracks in materials
• Physics:Peridynamics
• Computer simulation – Process of mathematical modelling, performed on a computer
• Discrete element method – Numerical methods for computing the motion and effect of a large number of small particles
• Cellular automaton – Discrete model studied in computer science
• Finite element method – Numerical method for solving physical or engineering problems
• Finite difference method – Class of numerical techniques

References

• Psakhie, S.G.; Horie, Y.; Korostelev, S.Yu.; Smolin, A.Yu.; Dmitriev, A.I.; Shilko, E.V.; Alekseev, S.V. (November 1995). "Method of movable cellular automata as a tool for simulation within the framework of mesomechanics". Russian Physics Journal 38 (11): 1157–1168. doi:10.1007/BF00559396. Bibcode: 1995RuPhJ..38.1157P. 
• Psakhie, S.G.; Korostelev, S.Y.; Smolin, A.Y.; Dmitriev, A.I.; Shilko, E.V.; Moiseenko D.D.; Tatarincev E.M.; Alekseev, S.V. (1998). "Movable cellular automata method as a tool for physical mesomechanics of materials". Physical Mesomechanics 1 (1): 95–108.  (Псахье, С.Г.; Коростелев, С.Ю.; Смолин, А.Ю.; Дмитриев, А.И.; Шилько, Е.В.; Моисеенко, Д.Д.; Татаринцев, Е.М.; Алексеев, С.В. (1998). "Метод подвижных клеточных автоматов как инструмент физической мезомеханики материалов". Физическая мезомеханика 1 (1): 95–108. https://elibrary.ru/item.asp?id=12913617. Retrieved 2010-03-03. )
• Psakhie, S.G.; Ostermeyer, G.P.; Dmitriev, A.I.; Shilko, E.V.; Smolin, A.Y.; Korostelev, S.Y. (2000). "Movable cellular automata method as new direction in numerical discrete mechanics. I. Theoretical description". Physical Mesomechanics 3 (2): 5–13.  (Псахье, С.Г.; Остермайер, Г.П.; Дмитриев, А.И.; Шилько, Е.В.; Смолин, А.Ю.; Коростелев, С.Ю. (2000). "Метод подвижных клеточных автоматов как новое направление дискретной вычислительной механики. I. Теоретическое описание". Физическая мезомеханика 3 (2): 5–13. https://elibrary.ru/item.asp?id=12913646. Retrieved 2010-03-03. )
• Psakhie, S.G.; Horie, Y.; Ostermeyer, G.P.; Korostelev, S.Yu.; Smolin, A.Yu.; Shilko, E.V.; Dmitriev, A.I.; Blatnik, S. et al. (December 2001). "Movable cellular automata method for simulating materials with mesostructure". Theoretical and Applied Fracture Mechanics 37 (1–3): 311–334. doi:10.1016/S0167-8442(01)00079-9. http://mechanik.tu-berlin.de/popov/software/mca/TAFMEC.pdf. 
• Psakhie, S.G.; Smolin, A.Y.; Stefanov, Y.P.; Makarov, P.V.; Chertov, M.A. (2004). "Modeling the behavior of complex media by jointly using discrete and continuum approaches". Technical Physics Letters 30 (9): 712–714. doi:10.1134/1.1804572. Bibcode: 2004TePhL..30..712P. https://zenodo.org/record/1163164. 
• Shimizu, Y.; Hart, R.; Cundall, P. (2004). Numerical modeling in Micromechanics via Particle Methods. ISBN 978-90-5809-679-1. https://books.google.com/books?id=GVAUH98Yr6oC&dq=%22Movable+cellular+automaton%22+-inpublisher%3Aicon&pg=PR4. Retrieved 2010-03-03. 
• Gnecco, E., ed (2007). Fundamentals of friction and wear on the Nanoscale. ISBN 978-3-540-36806-9. https://books.google.com/books?id=v2Pe5thhNiwC&pg=PP1. Retrieved 2010-03-03. 
• Yunliang, Tan; Guirong, Teng; Haitao, Li (2008). "MCA Model for Simulating the Failure of Microinhomogeneous Materials". Journal of Nanomaterials 2008: 1–7. doi:10.1155/2008/946038. 946038. 
• Fomin, V.M. et al. (2008). Mechanics - from discrete to continuous. Russian academy of science, Siberian branch, Institute of theoretical and applied mechanics (named S.A. Khristianovich). p. 344. ISBN 978-5-7692-0974-1.  (Фомин, В.М.; Андреев А.Н. и др. (2008) (in ru). Механика - от дискретного к сплошному. Рос. акад наук, Сиб. отд-ние, Ин-т теоретической и прикладной механики им. С.А. Христиановича. p. 344. ISBN 978-5-7692-0974-1. http://www.sibran.ru/psb/books/show_text.phtml?rus+1880+psb. Retrieved 3 March 2010. )
• Smolin, A.Y.; Roman, N.V.; Dobrynin, S.A.; Psakhie, S.G. (May–August 2009). "On rotation in the movable cellular automaton method". Physical Mesomechanics 12 (3–4): 124–129. doi:10.1016/j.physme.2009.07.004. 
• Popov, Valentin L. (2009). Kontaktmechanik und Reibung (Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation). Springer Berlin Heidelberg. doi:10.1007/978-3-540-88837-6. ISBN 978-3-540-88836-9. 
• Dobrynin, S.A. (2010). Development of movable cellular atomaton method for modeling generation and propagation of elastic waves under contact interaction of solids. Tomsk: PhD thesis in physics and mathematics. p. 130.  (Добрынин, С.А. (2010) (in ru). Развитие метода подвижных клеточных автоматов для моделирования генерации и распространения упругих волн при контактном взаимодействии твердых тел. Томск: Диссертация … кандидата физико-математических наук. p. 130. http://serg-dobrinin.narod.ru/disert/index.html. Retrieved 3 March 2010. )
• Dobrynin, Sergey (2011). Computer simulation by movable cellular automaton method. Saarbrücken Germany: LAP LAMBERT Academic Publishing. p. 132. ISBN 978-3-8443-5954-1.  (Добрынин, Сергей (2011) (in ru). Компьютерное моделирование методом подвижных клеточных автоматов. Saarbrücken Germany: LAP LAMBERT Academic Publishing. p. 132. ISBN 978-3-8443-5954-1. https://www.lap-publishing.com/catalog/details/store/gb/book/978-3-8443-5954-1/%D0%9A%D0%BE%D0%BC%D0%BF%D1%8C%D1%8E%D1%82%D0%B5%D1%80%D0%BD%D0%BE%D0%B5-%D0%BC%D0%BE%D0%B4%D0%B5%D0%BB%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5-%D0%BC%D0%B5%D1%82%D0%BE%D0%B4%D0%BE%D0%BC-%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D1%85-%D0%BA%D0%BB%D0%B5%D1%82%D0%BE%D1%87%D0%BD%D1%8B%D1%85-%D0%B0%D0%B2%D1%82%D0%BE%D0%BC%D0%B0%D1%82%D0%BE%D0%B2. Retrieved 2011-11-19. )

Software

• MCA software package
• Software for simulation of materials in discrete-continuous approach «FEM+MCA»: Number of state registration in Applied Research Foundation of Algorithms and Software (AFAS): 50208802297 / Smolin A.Y., Zelepugin S.A., Dobrynin S.A.; applicant and development center is Tomsk State University. – register date 28.11.2008; certificate AFAS N 11826 date 01.12.2008.