Physics:Rise in core
The rise in core (RIC) method is an alternate reservoir wettability characterization method described by S. Ghedan and C. H. Canbaz in 2014. The method enables estimation of all wetting regions such as strongly water wet, intermediate water, oil wet and strongly oil wet regions in relatively quick and accurate measurements in terms of Contact angle rather than wettability index.
During the RIC experiments, core samples saturated with selected reservoir fluid were subjected to imbibition from a second reservoir fluid. RIC wettability measurements are compared with and modified – Amott test[1] and USBM measurements using core plug pairs from different heights of a thick carbonate reservoir. Results show good coherence. The RIC method is an alternate method to Amott and USBM methods and that efficiently characterizes Reservoir Wettability.[2][3]
Cut-off values vs wettability index
One study used the water advancing contact angle to estimate the wettability of fifty-five oil reservoirs. De-oxygenated synthetic formation brine and dead anaerobic crude was tested on quartz and calcite crystals at reservoir temperature. Contact angles from 0 to 75 degrees were deemed water wet, 75 to 105 degrees as intermediate and 105 to 180 degrees as oil wet.[4] Although the range of wettabilities were divided into three regions, these were arbitrary divisions. The wettability of different reservoirs can vary within the broad spectrum from strongly water-wet to strongly oil-wet.
Another study described two initial conditions as reference and non-reference for calculating cut-off values by using advancing and receding contact angles and spontaneous imbibition data.[5] Limiting value between water wet and intermediate zones was described as 62-degree. Similarly, cut-off values for advancing contact angle is described as 0 to 62 degrees for water wet region, 62 to 133 degrees for Intermediate-wet zone, and 133 to 180 degrees for Oil wet zone. Chilingar and Yen[6] examined extensive research work on 161 limestone, dolomitic limestone, calcitic dolomite, and dolomite cores. Cut-off values classified as 160 to 180 degrees for strongly oil wet, 100 to 160 degrees for oil wet, 80 to 100 degrees intermediate wet, 80 to 20 degrees water wet and 0 to 20 strongly water wet.
Rise in core uses a combination of Chilingar et al. and Morrow wettability cut-off criteria. The contact angle range 80 – 100 degrees indicate neutral-wetness, the range 100 – 133 degrees indicate slight-oil wetness, the range 133 – 160 degrees indicate oil-wetness while the range 160- 180 degrees indicate strongly oil-wetness. The range 62 – 80 degrees indicate slight water wetness, the range 20 – 62 degrees indicate, water-wetness, while the range 0 – 20 degrees indicate strong water-wetness.
Technique
RIC wettability characterization technique is based on a modified form of Washburn's equation (1921). The technique enables relatively quick and accurate measurements of wettability in terms of contact angle while requiring no complex equipment. The method is applicable for any set of reservoir fluids, on any type of reservoir rock and at any heterogeneity level. It characterizes wettability across the board from strongly water to strongly oil wet conditions.[7]
The step of deriving the modified form of Washburn equation for a rock/liquid/liquid system involves acquiring a Washburn equation for a rock/air/liquid system. The Washburn equation for a rock/air/liquid system is represented by:
- [math]\displaystyle{ t= {\mu \over C \rho^2 \gamma \cos \theta} {m^2} }[/math] (Eq.1).
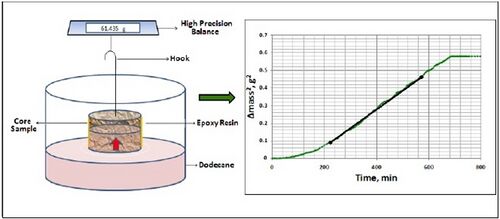
Herein, "t" is the penetration rate of liquid into a porous sample, "μ" is the liquid's viscosity, "ρ" is the liquid's density, "γ" is the liquid's surface tension, "θ" is the liquid's contact angle, "m" is the mass of the liquid that penetrates the porous sample and "C" is the constant of characterization of the porous sample. evaluating a value of "γos" using a young’s equation for a rock surface/water/air system (Figure 2) and a value of "γws" using young’s equation for a liquid/liquid/rock system is represented as:
- [math]\displaystyle{ \gamma_{ow} \cos \theta = \gamma_{os} \gamma_{ws} }[/math] (Eq.2).
"γow" is the surface tension between the oil and water system, "γos" is the surface tension between oil and solid system and "γws" is the surface tension between water and the solid system. Using Young's equation for a rock surface/ water/air system and substituting in equation (2) to obtain equation 3:
- [math]\displaystyle{ \cos\theta_{wo}= {{\gamma_o \cos \theta_o}\cdot{\gamma_w \cos \theta_w} \over {\gamma_{wo}}} }[/math] (Eq. 3).
Rearranging equation (1) to factor out γLV obtains equation (4), wherein γLV a liquid-vapor surface tension is:
- [math]\displaystyle{ \gamma_{LV}= {\mu \over C \rho^2 \gamma \cos \theta} \cdot {m^2 \over t} }[/math] (Eq. 4).
Realizing that γLV (liquid–vapor surface tension) is equivalent to γo (oil–air surface tension), or γw (water–air-surface tension), substituting equation (4) in equation (3) and cancelling out similar terms obtains equation (5):
- [math]\displaystyle{ \cos \theta_{wo}= {{({{m^2 \mu_o} \over {C {\rho_o}^2 t}})-({{m^2 \mu_w} \over {C {\rho_w}^2 t}})} \over \mu_{wo} } }[/math] (Eq. 5).
Therein, γLV is liquid-vapor surface tension, γois oil-air surface tension, γw is water-air surface tension, µo is viscosity of oil and µw is viscosity of water. cosθwo is contact angle between water and oil; representing a relationship between a mass of water imbibed into the core sample and a mass of oil imbibed in the core sample with an equation (6):
- [math]\displaystyle{ {\rho_w g V_w} = {\rho_o g V_o} }[/math] (Eq. 6).
Therein ρw is density of water and Vw is volume of water imbibed, ρo is density of oil and Vo is volume of oil imbibed, the amount of water imbibed and amount of oil imbibed under gravity are same; and air behaves as a strong non-wetting phase in both an oil–air–solid and a water–air–solid systems, thereby indicating that both oil and water behave as strong wetting phases, resulting in equal air/oil and air/water capillary forces for the same porous media and for a given pore size distribution. Thus, a mass change of a core sample due to water imbibition is equal to a mass change of a core sample due to oil imbibition, because water or oil penetration of the porous media at any time is a function of a balance between gravity and capillary forces. The mass of water imbibed into a core sample is approximately equal to a mass of oil imbibed in the core sample core samples of a same rock type and dimensions, and for equal capillary forces;
Cancelling out g in equation(6) gives equation (7):
- [math]\displaystyle{ {\rho_w V_w} = {\rho_o V_o} }[/math] (Eq. 7),
which means
- [math]\displaystyle{ {m_w} = {m_o} }[/math] (Eq. 8).
Therein, mw is mass of water and mo is mass of oil. Factoring out [math]\displaystyle{ C {m^2 \over t} }[/math] from Eq. 5 to obtain Eq. 9, gives Modified Washburn Equation:
- [math]\displaystyle{ {\cos \theta_{12}} = {{{{(\mu_1 {\rho_2}^2)}-{(\mu_2 {\rho_1}^2)}}\over {{{\rho_1}^2} {{\rho_2}^2} C \mu_{L1L2}}} \cdot \left({m^2 \over t}\right)} }[/math] (Eq. 9).
Therein θ12 is the contact angle of liquid/liquid/rock system, μ1 is a viscosity of oil phase, μ2 is a viscosity of water phase, ρ1 is density of oil phase in g/cm3, ρ2 is density of water phase in g/cm3, m is mass of fluid penetrated into a porous rock, t is time in min, γ_L1L2 is the surface tension between an oil and a water in dyne/cm, and ∁ is a characteristic constant of the porous rock.
Experimental setup and procedure
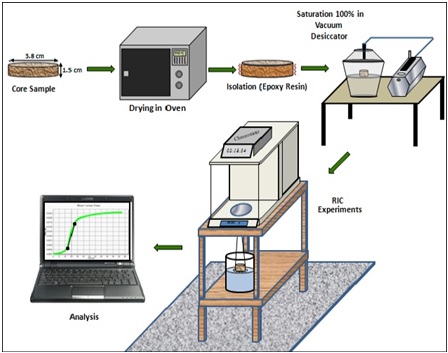
Schematic view and experimental setups of the RIC wettability testing method is described in Figure 1. Core plugs are divided into 3–4 core samples, each of 3.8 cm average diameter and 1.5 cm length. The lateral area of each core sample is sealed by epoxy resin to ensure one-dimensional liquid penetration into the core by imbibition. A hook is mounted on top side of the core sample.
The RIC setup includes a beaker to host the imbibing fluid. A thin rope connects the core sample to a high-precision balance (0.001 gm accurate). A hanging core sample is positioned with the bottom part of the sample barely touching the imbibing fluid in the beaker. Relative saturation as well as mass of core samples starts to change during imbibition. A computer connected to a balance continuously monitors the core sample mass change over time. Plots of squared mass change versus time are generated.[2][8]
Determination of "C" constant
The RIC experiment is first performed with a n-dodecane–air–rock system to determine the constant ∁ of the Washburn Equation. N-dodecane imbibes into one of the core samples and the imbibition curve is recorded in Figure 2. Dodecane is an alkane that has low surface energy, very strongly wetting the rock sample in the presence of air, with contact angle θ equal to zero. Constant ∁ is determined by the contact angle value for dodecane/air/rock system, determining physical properties of n-dodecane (ρ,μ,γ) and rearranging equation 1;
- [math]\displaystyle{ C= {\mu \over \rho^2 \gamma_{LV} \cos \theta} \cdot {m^2 \over t} }[/math] (Eq. 10)
Experiment
The second step of the RIC experimental process is to saturate the neighboring core sample with crude oil and subjected the sample to water imbibition. Applying the slope of the RIC curve [math]\displaystyle{ ({m^2 \over t}) }[/math], fluid properties of oil/brine system (ρ,μ,γ) and the ∁ value are determined from the neighboring core sample into Eq. 9 to calculate the contact angle, θ.
References
- ↑ Amott, E. (1959). "Observations related to Wettability of Porous Rock". AIME. pp. 216, 156–162. https://www.onepetro.org/general/SPE-1167-G.
- ↑ Jump up to: 2.0 2.1 Ghedan, Shawket G.; Canbaz, Celal Hakan (19 January 2014) (in en). Theory and Experimental Setup of the New Rise in Core Reservoir Wettability Measurement Technique. doi:10.2523/iptc-17659-ms. ISBN 9781613993224.
- ↑ US patent patent 20120136578
- ↑ Treiber, L.E.; Owens, W.W. (1 December 1972). "A Laboratory Evaluation of the Wettability of Fifty Oil-Producing Reservoirs" (in en). Society of Petroleum Engineers Journal 12 (6): 531–540. doi:10.2118/3526-pa. ISSN 0197-7520.
- ↑ Ma, S.M.; Zhang, X.; Morrow, N.R.; Zhou, X. (1 December 1999). "Characterization of Wettability From Spontaneous Imbibition Measurements" (in en). Journal of Canadian Petroleum Technology 38 (13): 49. doi:10.2118/99-13-49. ISSN 0021-9487. Bibcode: 1999BCaPG..38.1349M.
- ↑ Chilingar, George V.; Yen, T. F. (1 January 1983). "Some Notes on Wettability and Relative Permeabilities of Carbonate Reservoir Rocks, II". Energy Sources 7 (1): 67–75. doi:10.1080/00908318308908076. ISSN 0090-8312.
- ↑ Ghedan, Shawkat G.; Canbaz, Celal Hakan; Boyd, Douglas A.; Mani, George M.; Haggag, Marwan Khamis (1 January 2010). "Wettability Profile of a Thick Carbonate Reservoir by the New Rise in Core Wettability Characterization Method" (in en). All Days. doi:10.2118/138697-ms. ISBN 9781555633158.
- ↑ Canbaz, C.H., Ghedan, S.G., "Theory and Experimental Setup of the New Rise in Core Reservoir Wettability Measurement Technique" IPTC #17659, IPTC, Doha, Qatar, January 2014.
- Brown, Jeffrey S. (31 December 2013). Compositional simulation model for carbon dioxide flooding with improved fluid trapping, A. Colorado School of Mines (Thesis).
- Luo, Peng; Li, Sheng (2017). "Simultaneous Capillary Pressure and Wettability Determination for Tight Bakken Cores Using an Ultra-High-Speed Centrifuge". SPE Unconventional Resources Conference. doi:10.2118/185067-MS.
- Klewiah, Isaac (30 July 2018). Adsorption of Polar Oil Components onto Chalk: Impact of Silica content on Initial Wetting. University of Stavanger (Master thesis).
- Smajla, Ivan (21 September 2017). Usporedba različitih metoda analiza močivosti i relativnih propusnosti stijena i njihov utjecaj na iscrpak ugljikovodika iz novog naftnog ležišta u Savskoj depresiji. Croatian Digital Theses Repository (info:eu-repo/semantics/masterThesis).
- Seid Mohammadi, M.; Moghadasi, J.; Naseri, S. (2014). "An experimental investigation of wettability alteration in carbonate reservoir using γ-Al2O3 nanoparticles". Iranian Journal of Oil & Gas Science and Technology 3 (2): 18–26. doi:10.22050/ijogst.2014.6034.
- Bassioni, Ghada; Taha Taqvi, Syed (2015). "Wettability Studies Using Zeta Potential Measurements". Journal of Chemistry 2015: 1–6. doi:10.1155/2015/743179. http://pdfs.semanticscholar.org/eb03/059a1c64e339b2744f475c65d9f04f247b32.pdf.
- Sprunt, E. S.; Collins, S. H. (1991). "U.S. Patent No. 5,069,065.". Washington, DC: U.S. Patent and Trademark Office. https://patents.google.com/patent/US5069065A/en.
- Taqvi, Syed Taha; Almansoori, Ali; Bassioni, Ghada (2016). "Understanding the Role of Asphaltene in Wettability Alteration Using ζ Potential Measurements". Energy Fuels 30 (3): 1927–1932. doi:10.1021/acs.energyfuels.5b02127.
- c. Ferreira, Flavio; Stukan, Mikhail; Liang, Lin; Souza, Andre; Venkataramanan, Lalitha; Beletskaya, Anna; Dias, Daniel; Dantas Da Silva, Marianna (2018). "New Model for Wettability Change with Depth in Mixed-Wet Complex Carbonates". Abu Dhabi International Petroleum Exhibition & Conference. doi:10.2118/192758-MS.
- Seiedi, Omolbanin; Zahedzadeh, Mohammad; Roayaei, Emad; Aminnaji, Morteza; Fazeli, Hossein (2020). "Experimental and modeling study of wettability alteration through seawater injection in limestone: a case study". Petroleum Science 17 (3): 749–758. doi:10.1007/s12182-019-00407-y. Bibcode: 2020PetSc..17..749S.
- "Rise in core wettability characterization method". https://patents.google.com/patent/US8768628B2/en.
- Canbaz, C. H.; Ghedan, S. (2015). "Wettability characterization of different oil/brine/rock systems by using Rise in Core method". 20th international petroleum and natural gas congress and exhibition (IPETGAS). Turkey. pp. 365–370. https://www.researchgate.net/publication/319306019.
 |