Projection (linear algebra)

Short description: Idempotent linear transformation from a vector space to itself

The transformation P is the orthogonal projection onto the line m.

In linear algebra and functional analysis, a projection is a linear transformation [math]\displaystyle{ P }[/math] from a vector space to itself (an endomorphism) such that [math]\displaystyle{ P\circ P=P }[/math]. That is, whenever [math]\displaystyle{ P }[/math] is applied twice to any vector, it gives the same result as if it were applied once (i.e. [math]\displaystyle{ P }[/math] is idempotent). It leaves its image unchanged. This definition of "projection" formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object.

Definitions

A projection on a vector space [math]\displaystyle{ V }[/math] is a linear operator [math]\displaystyle{ P\colon V \to V }[/math] such that [math]\displaystyle{ P^2 = P }[/math].

When [math]\displaystyle{ V }[/math] has an inner product and is complete, i.e. when [math]\displaystyle{ V }[/math] is a Hilbert space, the concept of orthogonality can be used. A projection [math]\displaystyle{ P }[/math] on a Hilbert space [math]\displaystyle{ V }[/math] is called an orthogonal projection if it satisfies [math]\displaystyle{ \langle P \mathbf x, \mathbf y \rangle = \langle \mathbf x, P \mathbf y \rangle }[/math] for all [math]\displaystyle{ \mathbf x, \mathbf y \in V }[/math]. A projection on a Hilbert space that is not orthogonal is called an oblique projection.

Projection matrix

• A square matrix [math]\displaystyle{ P }[/math] is called a projection matrix if it is equal to its square, i.e. if [math]\displaystyle{ P^2 = P }[/math].
• A square matrix [math]\displaystyle{ P }[/math] is called an orthogonal projection matrix if [math]\displaystyle{ P^2 = P = P^{\mathrm T} }[/math] for a real matrix, and respectively [math]\displaystyle{ P^2 = P = P^{*} }[/math] for a complex matrix, where [math]\displaystyle{ P^{\mathrm T} }[/math] denotes the transpose of [math]\displaystyle{ P }[/math] and [math]\displaystyle{ P^{*} }[/math] denotes the adjoint or Hermitian transpose of [math]\displaystyle{ P }[/math].
• A projection matrix that is not an orthogonal projection matrix is called an oblique projection matrix.

The eigenvalues of a projection matrix must be 0 or 1.

Examples

Orthogonal projection

For example, the function which maps the point [math]\displaystyle{ (x,y,z) }[/math] in three-dimensional space [math]\displaystyle{ \mathbb{R}^3 }[/math] to the point [math]\displaystyle{ (x,y,0) }[/math] is an orthogonal projection onto the xy-plane. This function is represented by the matrix [math]\displaystyle{ P = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}. }[/math]

The action of this matrix on an arbitrary vector is [math]\displaystyle{ P \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} x \\ y \\ 0 \end{bmatrix}. }[/math]

To see that [math]\displaystyle{ P }[/math] is indeed a projection, i.e., [math]\displaystyle{ P = P^2 }[/math], we compute [math]\displaystyle{ P^2 \begin{bmatrix} x \\ y \\ z \end{bmatrix} = P \begin{bmatrix} x \\ y \\ 0 \end{bmatrix} = \begin{bmatrix} x \\ y \\ 0 \end{bmatrix} = P\begin{bmatrix} x \\ y \\ z \end{bmatrix}. }[/math]

Observing that [math]\displaystyle{ P^{\mathrm T} = P }[/math] shows that the projection is an orthogonal projection.

Oblique projection

A simple example of a non-orthogonal (oblique) projection is [math]\displaystyle{ P = \begin{bmatrix} 0 & 0 \\ \alpha & 1 \end{bmatrix}. }[/math]

Via matrix multiplication, one sees that [math]\displaystyle{ P^2 = \begin{bmatrix} 0 & 0 \\ \alpha & 1 \end{bmatrix} \begin{bmatrix} 0 & 0 \\ \alpha & 1 \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ \alpha & 1 \end{bmatrix} = P. }[/math] showing that [math]\displaystyle{ P }[/math] is indeed a projection.

The projection [math]\displaystyle{ P }[/math] is orthogonal if and only if [math]\displaystyle{ \alpha = 0 }[/math] because only then [math]\displaystyle{ P^{\mathrm T} = P. }[/math]

Properties and classification

The transformation T is the projection along k onto m. The range of T is m and the kernel is k.

Idempotence

By definition, a projection [math]\displaystyle{ P }[/math] is idempotent (i.e. [math]\displaystyle{ P^2 = P }[/math]).

Open map

Every projection is an open map, meaning that it maps each open set in the domain to an open set in the subspace topology of the image. That is, for any vector [math]\displaystyle{ \mathbf{x} }[/math] and any ball [math]\displaystyle{ B_\mathbf{x} }[/math] (with positive radius) centered on [math]\displaystyle{ \mathbf{x} }[/math], there exists a ball [math]\displaystyle{ B_{P\mathbf{x}} }[/math] (with positive radius) centered on [math]\displaystyle{ P\mathbf{x} }[/math] that is wholly contained in the image [math]\displaystyle{ P(B_\mathbf{x}) }[/math].

Complementarity of image and kernel

Let [math]\displaystyle{ W }[/math] be a finite-dimensional vector space and [math]\displaystyle{ P }[/math] be a projection on [math]\displaystyle{ W }[/math]. Suppose the subspaces [math]\displaystyle{ U }[/math] and [math]\displaystyle{ V }[/math] are the image and kernel of [math]\displaystyle{ P }[/math] respectively. Then [math]\displaystyle{ P }[/math] has the following properties:

1. [math]\displaystyle{ P }[/math] is the identity operator [math]\displaystyle{ I }[/math] on [math]\displaystyle{ U }[/math]: [math]\displaystyle{ \forall \mathbf x \in U: P \mathbf x = \mathbf x. }[/math]
2. We have a direct sum [math]\displaystyle{ W = U \oplus V }[/math]. Every vector [math]\displaystyle{ \mathbf x \in W }[/math] may be decomposed uniquely as [math]\displaystyle{ \mathbf x = \mathbf u + \mathbf v }[/math] with [math]\displaystyle{ \mathbf u = P \mathbf x }[/math] and [math]\displaystyle{ \mathbf v = \mathbf x - P \mathbf x = \left(I-P\right) \mathbf x }[/math], and where [math]\displaystyle{ \mathbf u \in U, \mathbf v \in V. }[/math]

The image and kernel of a projection are complementary, as are [math]\displaystyle{ P }[/math] and [math]\displaystyle{ Q = I - P }[/math]. The operator [math]\displaystyle{ Q }[/math] is also a projection as the image and kernel of [math]\displaystyle{ P }[/math] become the kernel and image of [math]\displaystyle{ Q }[/math] and vice versa. We say [math]\displaystyle{ P }[/math] is a projection along [math]\displaystyle{ V }[/math] onto [math]\displaystyle{ U }[/math] (kernel/image) and [math]\displaystyle{ Q }[/math] is a projection along [math]\displaystyle{ U }[/math] onto [math]\displaystyle{ V }[/math].

Spectrum

In infinite-dimensional vector spaces, the spectrum of a projection is contained in [math]\displaystyle{ \{ 0, 1 \} }[/math] as [math]\displaystyle{ (\lambda I - P)^{-1} = \frac 1 \lambda I + \frac 1 {\lambda(\lambda-1)} P. }[/math] Only 0 or 1 can be an eigenvalue of a projection. This implies that an orthogonal projection [math]\displaystyle{ P }[/math] is always a positive semi-definite matrix. In general, the corresponding eigenspaces are (respectively) the kernel and range of the projection. Decomposition of a vector space into direct sums is not unique. Therefore, given a subspace [math]\displaystyle{ V }[/math], there may be many projections whose range (or kernel) is [math]\displaystyle{ V }[/math].

If a projection is nontrivial it has minimal polynomial [math]\displaystyle{ x^2 - x = x (x-1) }[/math], which factors into distinct linear factors, and thus [math]\displaystyle{ P }[/math] is diagonalizable.

Product of projections

The product of projections is not in general a projection, even if they are orthogonal. If two projections commute then their product is a projection, but the converse is false: the product of two non-commuting projections may be a projection.

If two orthogonal projections commute then their product is an orthogonal projection. If the product of two orthogonal projections is an orthogonal projection, then the two orthogonal projections commute (more generally: two self-adjoint endomorphisms commute if and only if their product is self-adjoint).

Orthogonal projections

When the vector space [math]\displaystyle{ W }[/math] has an inner product and is complete (is a Hilbert space) the concept of orthogonality can be used. An orthogonal projection is a projection for which the range [math]\displaystyle{ U }[/math] and the kernel [math]\displaystyle{ V }[/math] are orthogonal subspaces. Thus, for every [math]\displaystyle{ \mathbf x }[/math] and [math]\displaystyle{ \mathbf y }[/math] in [math]\displaystyle{ W }[/math], [math]\displaystyle{ \langle P \mathbf x, (\mathbf y - P \mathbf y) \rangle = \langle (\mathbf x - P \mathbf x) , P \mathbf y \rangle = 0 }[/math]. Equivalently: [math]\displaystyle{ \langle \mathbf x, P \mathbf y \rangle = \langle P \mathbf x, P \mathbf y \rangle = \langle P \mathbf x, \mathbf y \rangle. }[/math]

A projection is orthogonal if and only if it is self-adjoint. Using the self-adjoint and idempotent properties of [math]\displaystyle{ P }[/math], for any [math]\displaystyle{ \mathbf x }[/math] and [math]\displaystyle{ \mathbf y }[/math] in [math]\displaystyle{ W }[/math] we have [math]\displaystyle{ P\mathbf{x} \in U }[/math], [math]\displaystyle{ \mathbf{y} - P\mathbf{y} \in V }[/math], and [math]\displaystyle{ \langle P \mathbf x, \mathbf y - P \mathbf y \rangle = \langle \mathbf x, \left(P-P^2\right) \mathbf y \rangle = 0 }[/math] where [math]\displaystyle{ \langle \cdot, \cdot \rangle }[/math] is the inner product associated with [math]\displaystyle{ W }[/math]. Therefore, [math]\displaystyle{ P }[/math] and [math]\displaystyle{ I - P }[/math] are orthogonal projections. The other direction, namely that if [math]\displaystyle{ P }[/math] is orthogonal then it is self-adjoint, follows from the implication from [math]\displaystyle{ \langle (\mathbf x - P \mathbf x) , P \mathbf y \rangle = \langle P \mathbf x, (\mathbf y - P \mathbf y) \rangle = 0 }[/math] to [math]\displaystyle{ \langle \mathbf x, P \mathbf y \rangle = \langle P \mathbf x, P\mathbf y \rangle = \langle P \mathbf x, \mathbf y \rangle = \langle \mathbf x, P^* \mathbf y \rangle }[/math] for every [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] in [math]\displaystyle{ W }[/math]; thus [math]\displaystyle{ P=P^* }[/math].

The existence of an orthogonal projection onto a closed subspace follows from the Hilbert projection theorem.

Properties and special cases

An orthogonal projection is a bounded operator. This is because for every [math]\displaystyle{ \mathbf v }[/math] in the vector space we have, by the Cauchy–Schwarz inequality: [math]\displaystyle{ \left \| P \mathbf v\right\|^2 = \langle P \mathbf v, P \mathbf v \rangle = \langle P \mathbf v, \mathbf v \rangle \leq \left\|P \mathbf v\right\| \cdot \left\|\mathbf v\right\| }[/math] Thus [math]\displaystyle{ \left\|P \mathbf v\right\| \leq \left\|\mathbf v\right\| }[/math].

For finite-dimensional complex or real vector spaces, the standard inner product can be substituted for [math]\displaystyle{ \langle \cdot, \cdot \rangle }[/math].

Formulas

A simple case occurs when the orthogonal projection is onto a line. If [math]\displaystyle{ \mathbf u }[/math] is a unit vector on the line, then the projection is given by the outer product [math]\displaystyle{ P_\mathbf{u} = \mathbf u \mathbf u^\mathsf{T}. }[/math] (If [math]\displaystyle{ \mathbf u }[/math] is complex-valued, the transpose in the above equation is replaced by a Hermitian transpose). This operator leaves u invariant, and it annihilates all vectors orthogonal to [math]\displaystyle{ \mathbf u }[/math], proving that it is indeed the orthogonal projection onto the line containing u. A simple way to see this is to consider an arbitrary vector [math]\displaystyle{ \mathbf x }[/math] as the sum of a component on the line (i.e. the projected vector we seek) and another perpendicular to it, [math]\displaystyle{ \mathbf x = \mathbf x_\parallel + \mathbf x_\perp }[/math]. Applying projection, we get [math]\displaystyle{ P_{\mathbf u} \mathbf x = \mathbf u \mathbf u^\mathsf{T} \mathbf x_\parallel + \mathbf u \mathbf u^\mathsf{T} \mathbf x_\perp = \mathbf u \left( \sgn\left(\mathbf u^\mathsf{T} \mathbf x_\parallel\right) \left \| \mathbf x_\parallel \right \| \right) + \mathbf u \cdot \mathbf 0 = \mathbf x_\parallel }[/math] by the properties of the dot product of parallel and perpendicular vectors.

This formula can be generalized to orthogonal projections on a subspace of arbitrary dimension. Let [math]\displaystyle{ \mathbf u_1, \ldots, \mathbf u_k }[/math] be an orthonormal basis of the subspace [math]\displaystyle{ U }[/math], with the assumption that the integer [math]\displaystyle{ k \geq 1 }[/math], and let [math]\displaystyle{ A }[/math] denote the [math]\displaystyle{ n \times k }[/math] matrix whose columns are [math]\displaystyle{ \mathbf u_1, \ldots, \mathbf u_k }[/math], i.e., [math]\displaystyle{ A = \begin{bmatrix} \mathbf u_1 & \cdots & \mathbf u_k \end{bmatrix} }[/math]. Then the projection is given by: [math]\displaystyle{ P_A = A A^\mathsf{T} }[/math] which can be rewritten as [math]\displaystyle{ P_A = \sum_i \langle \mathbf u_i, \cdot \rangle \mathbf u_i. }[/math]

The matrix [math]\displaystyle{ A^\mathsf{T} }[/math] is the partial isometry that vanishes on the orthogonal complement of [math]\displaystyle{ U }[/math], and [math]\displaystyle{ A }[/math] is the isometry that embeds [math]\displaystyle{ U }[/math] into the underlying vector space. The range of [math]\displaystyle{ P_A }[/math] is therefore the final space of [math]\displaystyle{ A }[/math]. It is also clear that [math]\displaystyle{ A A^{\mathsf T} }[/math] is the identity operator on [math]\displaystyle{ U }[/math].

The orthonormality condition can also be dropped. If [math]\displaystyle{ \mathbf u_1, \ldots, \mathbf u_k }[/math] is a (not necessarily orthonormal) basis with [math]\displaystyle{ k \geq 1 }[/math], and [math]\displaystyle{ A }[/math] is the matrix with these vectors as columns, then the projection is: [math]\displaystyle{ P_A = A \left(A^\mathsf{T} A\right)^{-1} A^\mathsf{T}. }[/math]

The matrix [math]\displaystyle{ A }[/math] still embeds [math]\displaystyle{ U }[/math] into the underlying vector space but is no longer an isometry in general. The matrix [math]\displaystyle{ \left(A^\mathsf{T}A\right)^{-1} }[/math] is a "normalizing factor" that recovers the norm. For example, the rank-1 operator [math]\displaystyle{ \mathbf u \mathbf u^\mathsf{T} }[/math] is not a projection if [math]\displaystyle{ \left\|\mathbf u \right\| \neq 1. }[/math] After dividing by [math]\displaystyle{ \mathbf u^\mathsf{T} \mathbf u = \left\| \mathbf u \right\|^2, }[/math] we obtain the projection [math]\displaystyle{ \mathbf u \left(\mathbf u^\mathsf{T} \mathbf u \right)^{-1} \mathbf u^\mathsf{T} }[/math] onto the subspace spanned by [math]\displaystyle{ u }[/math].

In the general case, we can have an arbitrary positive definite matrix [math]\displaystyle{ D }[/math] defining an inner product [math]\displaystyle{ \langle x, y \rangle_D = y^\dagger Dx }[/math], and the projection [math]\displaystyle{ P_A }[/math] is given by [math]\displaystyle{ P_A x = \operatorname{argmin}_{y \in \operatorname{range}(A)} \left\|x - y\right\|^2_D }[/math]. Then [math]\displaystyle{ P_A = A \left(A^\mathsf{T} D A\right)^{-1} A^\mathsf{T} D. }[/math]

When the range space of the projection is generated by a frame (i.e. the number of generators is greater than its dimension), the formula for the projection takes the form: [math]\displaystyle{ P_A = A A^+ }[/math]. Here [math]\displaystyle{ A^+ }[/math] stands for the Moore–Penrose pseudoinverse. This is just one of many ways to construct the projection operator.

If [math]\displaystyle{ \begin{bmatrix} A & B \end{bmatrix} }[/math] is a non-singular matrix and [math]\displaystyle{ A^\mathsf{T}B = 0 }[/math] (i.e., [math]\displaystyle{ B }[/math] is the null space matrix of [math]\displaystyle{ A }[/math]), the following holds: [math]\displaystyle{ \begin{align} I &= \begin{bmatrix} A & B \end{bmatrix} \begin{bmatrix} A & B \end{bmatrix}^{-1}\begin{bmatrix} A^\mathsf{T} \\ B^\mathsf{T} \end{bmatrix}^{-1} \begin{bmatrix} A^\mathsf{T} \\ B^\mathsf{T} \end{bmatrix} \\ &= \begin{bmatrix} A & B \end{bmatrix} \left( \begin{bmatrix} A^\mathsf{T} \\ B^\mathsf{T} \end{bmatrix} \begin{bmatrix} A & B \end{bmatrix} \right )^{-1} \begin{bmatrix} A^\mathsf{T} \\B^\mathsf{T} \end{bmatrix} \\ &= \begin{bmatrix} A & B \end{bmatrix} \begin{bmatrix}A^\mathsf{T}A&O\\O&B^\mathsf{T}B\end{bmatrix}^{-1} \begin{bmatrix} A^\mathsf{T} \\ B^\mathsf{T} \end{bmatrix}\\[4pt] &= A \left(A^\mathsf{T}A\right)^{-1} A^\mathsf{T} + B \left(B^\mathsf{T}B\right)^{-1} B^\mathsf{T} \end{align} }[/math]

If the orthogonal condition is enhanced to [math]\displaystyle{ A^\mathsf{T}W B = A^\mathsf{T}W^\mathsf{T}B = 0 }[/math] with [math]\displaystyle{ W }[/math] non-singular, the following holds: [math]\displaystyle{ I = \begin{bmatrix}A & B\end{bmatrix} \begin{bmatrix}\left(A^\mathsf{T} W A\right)^{-1} A^\mathsf{T} \\ \left(B^\mathsf{T} W B\right)^{-1} B^\mathsf{T} \end{bmatrix} W. }[/math]

All these formulas also hold for complex inner product spaces, provided that the conjugate transpose is used instead of the transpose. Further details on sums of projectors can be found in Banerjee and Roy (2014). Also see Banerjee (2004) for application of sums of projectors in basic spherical trigonometry.

Oblique projections

The term oblique projections is sometimes used to refer to non-orthogonal projections. These projections are also used to represent spatial figures in two-dimensional drawings (see oblique projection), though not as frequently as orthogonal projections. Whereas calculating the fitted value of an ordinary least squares regression requires an orthogonal projection, calculating the fitted value of an instrumental variables regression requires an oblique projection.

A projection is defined by its kernel and the basis vectors used to characterize its range (which is a complement of the kernel). When these basis vectors are orthogonal to the kernel, then the projection is an orthogonal projection. When these basis vectors are not orthogonal to the kernel, the projection is an oblique projection, or just a projection.

A matrix representation formula for a nonzero projection operator

Let [math]\displaystyle{ P }[/math] be a linear operator, [math]\displaystyle{ P : V \to V, }[/math] such that [math]\displaystyle{ P^2 = P }[/math] and assume that [math]\displaystyle{ P : V \to V }[/math] is not the zero operator. Let the vectors [math]\displaystyle{ \mathbf u_1, \ldots, \mathbf u_k }[/math] form a basis for the range of [math]\displaystyle{ P }[/math], and assemble these vectors in the [math]\displaystyle{ n \times k }[/math] matrix [math]\displaystyle{ A }[/math]. Therefore the integer [math]\displaystyle{ k \geq 1 }[/math], otherwise [math]\displaystyle{ k = 0 }[/math] and [math]\displaystyle{ P }[/math] is the zero operator. The range and the kernel are complementary spaces, so the kernel has dimension [math]\displaystyle{ n - k }[/math]. It follows that the orthogonal complement of the kernel has dimension [math]\displaystyle{ k }[/math]. Let [math]\displaystyle{ \mathbf v_1, \ldots, \mathbf v_k }[/math] form a basis for the orthogonal complement of the kernel of the projection, and assemble these vectors in the matrix [math]\displaystyle{ B }[/math]. Then the projection [math]\displaystyle{ P }[/math] (with the condition [math]\displaystyle{ k \geq 1 }[/math]) is given by [math]\displaystyle{ P = A \left(B^\mathsf{T} A\right)^{-1} B^\mathsf{T}. }[/math]

This expression generalizes the formula for orthogonal projections given above. A standard proof of this expression is the following. For any vector [math]\displaystyle{ \mathbf x }[/math] in the vector space [math]\displaystyle{ V }[/math], we can decompose [math]\displaystyle{ \mathbf{x} = \mathbf{x}_1 + \mathbf{x}_2 }[/math], where vector [math]\displaystyle{ \mathbf{x}_1 = P(\mathbf{x}) }[/math] is in the image of [math]\displaystyle{ P }[/math], and vector [math]\displaystyle{ \mathbf{x}_2 = \mathbf{x} - P(\mathbf{x}). }[/math] So [math]\displaystyle{ P(\mathbf{x}_2) = P(\mathbf{x}) - P^2(\mathbf{x})= \mathbf{0} }[/math], and then [math]\displaystyle{ \mathbf{x}_2 }[/math] is in the kernel of [math]\displaystyle{ P }[/math], which is the null space of [math]\displaystyle{ A. }[/math] In other words, the vector [math]\displaystyle{ \mathbf{x}_1 }[/math] is in the column space of [math]\displaystyle{ A, }[/math] so [math]\displaystyle{ \mathbf{x}_1 = A \mathbf{w} }[/math] for some [math]\displaystyle{ k }[/math] dimension vector [math]\displaystyle{ \mathbf{w} }[/math] and the vector [math]\displaystyle{ \mathbf{x}_2 }[/math] satisfies [math]\displaystyle{ B^\mathsf{T} \mathbf{x}_2=\mathbf{0} }[/math] by the construction of [math]\displaystyle{ B }[/math]. Put these conditions together, and we find a vector [math]\displaystyle{ \mathbf{w} }[/math] so that [math]\displaystyle{ B^\mathsf{T} (\mathbf{x}-A\mathbf{w})=\mathbf{0} }[/math]. Since matrices [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are of full rank [math]\displaystyle{ k }[/math] by their construction, the [math]\displaystyle{ k\times k }[/math]-matrix [math]\displaystyle{ B^\mathsf{T} A }[/math] is invertible. So the equation [math]\displaystyle{ B^\mathsf{T} (\mathbf{x}-A\mathbf{w})=\mathbf{0} }[/math] gives the vector [math]\displaystyle{ \mathbf{w}= (B^{\mathsf{T}}A)^{-1} B^{\mathsf{T}} \mathbf{x}. }[/math] In this way, [math]\displaystyle{ P\mathbf{x} = \mathbf{x}_1 = A\mathbf{w}= A(B^{\mathsf{T}}A)^{-1} B^{\mathsf{T}} \mathbf{x} }[/math] for any vector [math]\displaystyle{ \mathbf{x} \in V }[/math] and hence [math]\displaystyle{ P = A(B^{\mathsf{T}}A)^{-1} B^{\mathsf{T}} }[/math].

In the case that [math]\displaystyle{ P }[/math] is an orthogonal projection, we can take [math]\displaystyle{ A = B }[/math], and it follows that [math]\displaystyle{ P=A \left(A^\mathsf{T} A\right)^{-1} A^\mathsf{T} }[/math]. By using this formula, one can easily check that [math]\displaystyle{ P=P^\mathsf{T} }[/math]. In general, if the vector space is over complex number field, one then uses the Hermitian transpose [math]\displaystyle{ A^* }[/math] and has the formula [math]\displaystyle{ P=A \left(A^* A\right)^{-1} A^* }[/math]. Recall that one can define the Moore–Penrose inverse of the matrix [math]\displaystyle{ A }[/math] by [math]\displaystyle{ A^{+}= (A^*A)^{-1}A^* }[/math] since [math]\displaystyle{ A }[/math] has full column rank, so [math]\displaystyle{ P=A A^{+} }[/math].

Singular values

Note that [math]\displaystyle{ I-P }[/math] is also an oblique projection. The singular values of [math]\displaystyle{ P }[/math] and [math]\displaystyle{ I-P }[/math] can be computed by an orthonormal basis of [math]\displaystyle{ A }[/math]. Let [math]\displaystyle{ Q_A }[/math] be an orthonormal basis of [math]\displaystyle{ A }[/math] and let [math]\displaystyle{ Q_A^{\perp} }[/math] be the orthogonal complement of [math]\displaystyle{ Q_A }[/math]. Denote the singular values of the matrix [math]\displaystyle{ Q_A^T A (B^T A)^{-1} B^T Q_A^{\perp} }[/math] by the positive values [math]\displaystyle{ \gamma_1 \ge \gamma_2 \ge \ldots \ge \gamma_k }[/math]. With this, the singular values for [math]\displaystyle{ P }[/math] are: [math]\displaystyle{ \sigma_i = \begin{cases} \sqrt{1+\gamma_i^2} & 1 \le i \le k \\ 0 & \text{otherwise} \end{cases} }[/math] and the singular values for [math]\displaystyle{ I-P }[/math] are [math]\displaystyle{ \sigma_i = \begin{cases} \sqrt{1+\gamma_i^2} & 1 \le i \le k \\ 1 & k+1 \le i \le n-k \\ 0 & \text{otherwise} \end{cases} }[/math] This implies that the largest singular values of [math]\displaystyle{ P }[/math] and [math]\displaystyle{ I-P }[/math] are equal, and thus that the matrix norm of the oblique projections are the same. However, the condition number satisfies the relation [math]\displaystyle{ \kappa(I-P) = \frac{\sigma_1}{1} \ge \frac{\sigma_1}{\sigma_k} = \kappa(P) }[/math], and is therefore not necessarily equal.

Finding projection with an inner product

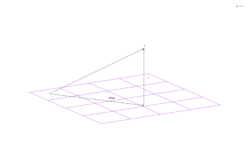
Let [math]\displaystyle{ V }[/math] be a vector space (in this case a plane) spanned by orthogonal vectors [math]\displaystyle{ \mathbf u_1, \mathbf u_2, \dots, \mathbf u_p }[/math]. Let [math]\displaystyle{ y }[/math] be a vector. One can define a projection of [math]\displaystyle{ \mathbf y }[/math] onto [math]\displaystyle{ V }[/math] as [math]\displaystyle{ \operatorname{proj}_V \mathbf y = \frac{\mathbf y \cdot \mathbf u^i}{\mathbf u^i \cdot \mathbf u^i } \mathbf u^i }[/math] where repeated indices are summed over (Einstein sum notation). The vector [math]\displaystyle{ \mathbf y }[/math] can be written as an orthogonal sum such that [math]\displaystyle{ \mathbf y = \operatorname{proj}_V \mathbf y + \mathbf z }[/math]. [math]\displaystyle{ \operatorname{proj}_V \mathbf y }[/math] is sometimes denoted as [math]\displaystyle{ \hat{\mathbf y} }[/math]. There is a theorem in linear algebra that states that this [math]\displaystyle{ \mathbf z }[/math] is the smallest distance (the orthogonal distance) from [math]\displaystyle{ \mathbf y }[/math] to [math]\displaystyle{ V }[/math] and is commonly used in areas such as machine learning.

y is being projected onto the vector space V.

Canonical forms

Any projection [math]\displaystyle{ P=P^2 }[/math] on a vector space of dimension [math]\displaystyle{ d }[/math] over a field is a diagonalizable matrix, since its minimal polynomial divides [math]\displaystyle{ x^2-x }[/math], which splits into distinct linear factors. Thus there exists a basis in which [math]\displaystyle{ P }[/math] has the form

[math]\displaystyle{ P = I_r\oplus 0_{d-r} }[/math]

where [math]\displaystyle{ r }[/math] is the rank of [math]\displaystyle{ P }[/math]. Here [math]\displaystyle{ I_r }[/math] is the identity matrix of size [math]\displaystyle{ r }[/math], [math]\displaystyle{ 0_{d-r} }[/math] is the zero matrix of size [math]\displaystyle{ d-r }[/math], and [math]\displaystyle{ \oplus }[/math] is the direct sum operator. If the vector space is complex and equipped with an inner product, then there is an orthonormal basis in which the matrix of P is

[math]\displaystyle{ P = \begin{bmatrix}1&\sigma_1 \\ 0&0\end{bmatrix} \oplus \cdots \oplus \begin{bmatrix}1&\sigma_k \\ 0&0\end{bmatrix} \oplus I_m \oplus 0_s. }[/math]

where [math]\displaystyle{ \sigma_1 \geq \sigma_2\geq \dots \geq \sigma_k \gt 0 }[/math]. The integers [math]\displaystyle{ k,s,m }[/math] and the real numbers [math]\displaystyle{ \sigma_i }[/math] are uniquely determined. Note that [math]\displaystyle{ 2k+s+m=d }[/math]. The factor [math]\displaystyle{ I_m \oplus 0_s }[/math] corresponds to the maximal invariant subspace on which [math]\displaystyle{ P }[/math] acts as an orthogonal projection (so that P itself is orthogonal if and only if [math]\displaystyle{ k=0 }[/math]) and the [math]\displaystyle{ \sigma_i }[/math]-blocks correspond to the oblique components.

Projections on normed vector spaces

When the underlying vector space [math]\displaystyle{ X }[/math] is a (not necessarily finite-dimensional) normed vector space, analytic questions, irrelevant in the finite-dimensional case, need to be considered. Assume now [math]\displaystyle{ X }[/math] is a Banach space.

Many of the algebraic results discussed above survive the passage to this context. A given direct sum decomposition of [math]\displaystyle{ X }[/math] into complementary subspaces still specifies a projection, and vice versa. If [math]\displaystyle{ X }[/math] is the direct sum [math]\displaystyle{ X = U \oplus V }[/math], then the operator defined by [math]\displaystyle{ P(u+v) = u }[/math] is still a projection with range [math]\displaystyle{ U }[/math] and kernel [math]\displaystyle{ V }[/math]. It is also clear that [math]\displaystyle{ P^2 = P }[/math]. Conversely, if [math]\displaystyle{ P }[/math] is projection on [math]\displaystyle{ X }[/math], i.e. [math]\displaystyle{ P^2 = P }[/math], then it is easily verified that [math]\displaystyle{ (1-P)^2 = (1-P) }[/math]. In other words, [math]\displaystyle{ 1 - P }[/math] is also a projection. The relation [math]\displaystyle{ P^2 = P }[/math] implies [math]\displaystyle{ 1 = P + (1-P) }[/math] and [math]\displaystyle{ X }[/math] is the direct sum [math]\displaystyle{ \operatorname{rg}(P) \oplus \operatorname{rg}(1 - P) }[/math].

However, in contrast to the finite-dimensional case, projections need not be continuous in general. If a subspace [math]\displaystyle{ U }[/math] of [math]\displaystyle{ X }[/math] is not closed in the norm topology, then the projection onto [math]\displaystyle{ U }[/math] is not continuous. In other words, the range of a continuous projection [math]\displaystyle{ P }[/math] must be a closed subspace. Furthermore, the kernel of a continuous projection (in fact, a continuous linear operator in general) is closed. Thus a continuous projection [math]\displaystyle{ P }[/math] gives a decomposition of [math]\displaystyle{ X }[/math] into two complementary closed subspaces: [math]\displaystyle{ X = \operatorname{rg}(P) \oplus \ker(P) = \ker(1-P) \oplus \ker(P) }[/math].

The converse holds also, with an additional assumption. Suppose [math]\displaystyle{ U }[/math] is a closed subspace of [math]\displaystyle{ X }[/math]. If there exists a closed subspace [math]\displaystyle{ V }[/math] such that X = U ⊕ V, then the projection [math]\displaystyle{ P }[/math] with range [math]\displaystyle{ U }[/math] and kernel [math]\displaystyle{ V }[/math] is continuous. This follows from the closed graph theorem. Suppose x_n → x and Px_n → y. One needs to show that [math]\displaystyle{ Px=y }[/math]. Since [math]\displaystyle{ U }[/math] is closed and {Px_n} ⊂ U, y lies in [math]\displaystyle{ U }[/math], i.e. Py = y. Also, x_n − Px_n = (I − P)x_n → x − y. Because [math]\displaystyle{ V }[/math] is closed and {(I − P)x_n} ⊂ V, we have [math]\displaystyle{ x-y \in V }[/math], i.e. [math]\displaystyle{ P(x-y)=Px-Py=Px-y=0 }[/math], which proves the claim.

The above argument makes use of the assumption that both [math]\displaystyle{ U }[/math] and [math]\displaystyle{ V }[/math] are closed. In general, given a closed subspace [math]\displaystyle{ U }[/math], there need not exist a complementary closed subspace [math]\displaystyle{ V }[/math], although for Hilbert spaces this can always be done by taking the orthogonal complement. For Banach spaces, a one-dimensional subspace always has a closed complementary subspace. This is an immediate consequence of Hahn–Banach theorem. Let [math]\displaystyle{ U }[/math] be the linear span of [math]\displaystyle{ u }[/math]. By Hahn–Banach, there exists a bounded linear functional [math]\displaystyle{ \varphi }[/math] such that φ(u) = 1. The operator [math]\displaystyle{ P(x)=\varphi(x)u }[/math] satisfies [math]\displaystyle{ P^2=P }[/math], i.e. it is a projection. Boundedness of [math]\displaystyle{ \varphi }[/math] implies continuity of [math]\displaystyle{ P }[/math] and therefore [math]\displaystyle{ \ker(P) = \operatorname{rg}(I-P) }[/math] is a closed complementary subspace of [math]\displaystyle{ U }[/math].

Applications and further considerations

Projections (orthogonal and otherwise) play a major role in algorithms for certain linear algebra problems:

• QR decomposition (see Householder transformation and Gram–Schmidt decomposition);
• Singular value decomposition
• Reduction to Hessenberg form (the first step in many eigenvalue algorithms)
• Linear regression
• Projective elements of matrix algebras are used in the construction of certain K-groups in Operator K-theory

As stated above, projections are a special case of idempotents. Analytically, orthogonal projections are non-commutative generalizations of characteristic functions. Idempotents are used in classifying, for instance, semisimple algebras, while measure theory begins with considering characteristic functions of measurable sets. Therefore, as one can imagine, projections are very often encountered in the context of operator algebras. In particular, a von Neumann algebra is generated by its complete lattice of projections.

Generalizations

More generally, given a map between normed vector spaces [math]\displaystyle{ T\colon V \to W, }[/math] one can analogously ask for this map to be an isometry on the orthogonal complement of the kernel: that [math]\displaystyle{ (\ker T)^\perp \to W }[/math] be an isometry (compare Partial isometry); in particular it must be onto. The case of an orthogonal projection is when W is a subspace of V. In Riemannian geometry, this is used in the definition of a Riemannian submersion.

See also

• Centering matrix, which is an example of a projection matrix.
• Dykstra's projection algorithm to compute the projection onto an intersection of sets
• Invariant subspace
• Least-squares spectral analysis
• Orthogonalization
• Properties of trace

References

• Banerjee, Sudipto; Roy, Anindya (2014), Linear Algebra and Matrix Analysis for Statistics, Texts in Statistical Science (1st ed.), Chapman and Hall/CRC, ISBN 978-1420095388 
• Dunford, N.; Schwartz, J. T. (1958). Linear Operators, Part I: General Theory. Interscience. 
• Meyer, Carl D. (2000). Matrix Analysis and Applied Linear Algebra. Society for Industrial and Applied Mathematics. ISBN 978-0-89871-454-8. http://www.matrixanalysis.com/. 

External links

• MIT Linear Algebra Lecture on Projection Matrices on YouTube, from MIT OpenCourseWare
• Linear Algebra 15d: The Projection Transformation on YouTube, by Pavel Grinfeld.
• Planar Geometric Projections Tutorial – a simple-to-follow tutorial explaining the different types of planar geometric projections.