Physics:Hubbard model

Short description: Approximate model used to describe the transition between conducting and insulating systems

2-dimensional Hubbard model.

The Hubbard model is an approximate model used to describe the transition between conducting and insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard.

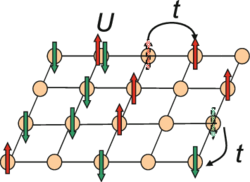
The Hubbard model states that each electron experiences competing forces: one pushes it to tunnel to neighboring atoms, while the other pushes it away from its neighbors. Its Hamiltonian thus has two terms: a kinetic term allowing for tunneling ("hopping") of particles between lattice sites and a potential term reflecting on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, in which case the model is referred to as the "Bose–Hubbard model".

The Hubbard model is a useful approximation for particles in a periodic potential at sufficiently low temperatures, where all the particles may be assumed to be in the lowest Bloch band, and long-range interactions between the particles can be ignored. If interactions between particles at different sites of the lattice are included, the model is often referred to as the "extended Hubbard model". In particular, the Hubbard term, most commonly denoted by U, is applied in first principles based simulations using Density Functional Theory, DFT. The inclusion of the Hubbard term in DFT simulations is important as this improves the prediction of electron localisation and thus it prevents the incorrect prediction of metallic conduction in insulating systems.

The Hubbard model introduces short-range interactions between electrons to the tight-binding model, which only includes kinetic energy (a "hopping" term) and interactions with the atoms of the lattice (an "atomic" potential). When the interaction between electrons is strong, the behavior of the Hubbard model can be qualitatively different from a tight-binding model. For example, the Hubbard model correctly predicts the existence of Mott insulators: materials that are insulating due to the strong repulsion between electrons, even though they satisfy the usual criteria for conductors, such as having an odd number of electrons per unit cell.

History

The model was originally proposed in 1963 to describe electrons in solids. Hubbard, Martin Gutzwiller and Junjiro Kanamori each independently proposed it.

Since then, it has been applied to the study of high-temperature superconductivity, quantum magnetism, and charge density waves.

Narrow energy band theory

The Hubbard model is based on the tight-binding approximation from solid-state physics, which describes particles moving in a periodic potential, typically referred to as a lattice. For real materials, each lattice site might correspond with an ionic core, and the particles would be the valence electrons of these ions. In the tight-binding approximation, the Hamiltonian is written in terms of Wannier states, which are localized states centered on each lattice site. Wannier states on neighboring lattice sites are coupled, allowing particles on one site to "hop" to another. Mathematically, the strength of this coupling is given by a "hopping integral", or "transfer integral", between nearby sites. The system is said to be in the tight-binding limit when the strength of the hopping integrals falls off rapidly with distance. This coupling allows states associated with each lattice site to hybridize, and the eigenstates of such a crystalline system are Bloch's functions, with the energy levels divided into separated energy bands. The width of the bands depends upon the value of the hopping integral.

The Hubbard model introduces a contact interaction between particles of opposite spin on each site of the lattice. When the Hubbard model is used to describe electron systems, these interactions are expected to be repulsive, stemming from the screened Coulomb interaction. However, attractive interactions have also been frequently considered. The physics of the Hubbard model is determined by competition between the strength of the hopping integral, which characterizes the system's kinetic energy, and the strength of the interaction term. The Hubbard model can therefore explain the transition from metal to insulator in certain interacting systems. For example, it has been used to describe metal oxides as they are heated, where the corresponding increase in nearest-neighbor spacing reduces the hopping integral to the point where the on-site potential is dominant. Similarly, the Hubbard model can explain the transition from conductor to insulator in systems such as rare-earth pyrochlores as the atomic number of the rare-earth metal increases, because the lattice parameter increases (or the angle between atoms can also change) as the rare-earth element atomic number increases, thus changing the relative importance of the hopping integral compared to the on-site repulsion.

Example: one dimensional hydrogen atom chain

The hydrogen atom has one electron, in the so-called s orbital, which can either be spin up ([math]\displaystyle{ \uparrow }[/math]) or spin down ([math]\displaystyle{ \downarrow }[/math]). This orbital can be occupied by at most two electrons, one with spin up and one down (see Pauli exclusion principle).

Under band theory, for a 1D chain of hydrogen atoms, the 1s orbital forms a continuous band, which would be exactly half-full. The 1D chain of hydrogen atoms is thus predicted to be a conductor under conventional band theory. This 1D string is the only configuration simple enough to be solved directly.

But in the case where the spacing between the hydrogen atoms is gradually increased, at some point the chain must become an insulator.

Expressed using the Hubbard model, the Hamiltonian is made up of two terms. The first term describes the kinetic energy of the system, parameterized by the hopping integral, [math]\displaystyle{ t }[/math]. The second term is the on-site interaction of strength [math]\displaystyle{ U }[/math] that represents the electron repulsion. Written out in second quantization notation, the Hubbard Hamiltonian then takes the form

[math]\displaystyle{ \hat{H} = -t \sum_{i,\sigma} \left( \hat{c}^\dagger_{i,\sigma} \hat{c}_{i+1,\sigma} + \hat{c}^\dagger_{i+1,\sigma} \hat{c}_{i,\sigma} \right) + U \sum_i \hat{n}_{i\uparrow} \hat{n}_{i\downarrow}, }[/math]

where [math]\displaystyle{ \hat{n}_{i\sigma} = \hat{c}_{i\sigma}^\dagger \hat{c}_{i\sigma} }[/math] is the spin-density operator for spin [math]\displaystyle{ \sigma }[/math] on the [math]\displaystyle{ i }[/math]-th site. The density operator is [math]\displaystyle{ \hat{n}_i = \hat{n}_{i \uparrow} + \hat{n}_{i\downarrow} }[/math] and occupation of [math]\displaystyle{ i }[/math]-th site for the wavefunction [math]\displaystyle{ \Phi }[/math] is [math]\displaystyle{ n_i = \langle \Phi \vert \hat{n}_i \vert \Phi \rangle }[/math]. Typically t is taken to be positive, and U may be either positive or negative, but is assumed to be positive when considering electronic systems.

Without the contribution of the second term, the Hamiltonian resolves to the tight binding formula from regular band theory.

Including the second term yields a realistic model that also predicts a transition from conductor to insulator as the ratio of interaction to hopping, [math]\displaystyle{ U/t }[/math], is varied. This ratio can be modified by, for example, increasing the inter-atomic spacing, which would decrease the magnitude of [math]\displaystyle{ t }[/math] without affecting [math]\displaystyle{ U }[/math]. In the limit where [math]\displaystyle{ U/t \gg 1 }[/math], the chain simply resolves into a set of isolated magnetic moments. If [math]\displaystyle{ U/t }[/math] is not too large, the overlap integral provides for superexchange interactions between neighboring magnetic moments, which may lead to a variety of interesting magnetic correlations, such as ferromagnetic, antiferromagnetic, etc. depending on the model parameters. The one-dimensional Hubbard model was solved by Lieb and Wu using the Bethe ansatz. Essential progress was achieved in the 1990s: a hidden symmetry was discovered, and the scattering matrix, correlation functions, thermodynamic and quantum entanglement were evaluated.

More complex systems

Although Hubbard is useful in describing systems such as a 1D chain of hydrogen atoms, it is important to note that more complex systems may experience other effects that the Hubbard model does not consider. In general, insulators can be divided into Mott–Hubbard insulators and charge-transfer insulators.

A Mott–Hubbard insulator can be described as

[math]\displaystyle{ (\mathrm{Ni}^{2+} \mathrm O^{2-})_2 \longrightarrow \mathrm{Ni}^{3+} \mathrm O^{2-} + \mathrm{Ni}^{1+} \mathrm{O}^{2-}. }[/math]

This can be seen as analogous to the Hubbard model for hydrogen chains, where conduction between unit cells can be described by a transfer integral.

However, it is possible for the electrons to exhibit another kind of behavior:

[math]\displaystyle{ \mathrm{Ni}^{2+} \mathrm O^{2-} \longrightarrow \mathrm{Ni}^{1+} \mathrm O^{1-}. }[/math]

This is known as charge transfer and results in charge-transfer insulators. Unlike Mott–Hubbard insulators electron transfer happens only within a unit cell.

Both of these effects may be present and compete in complex ionic systems.

Numerical treatment

The fact that the Hubbard model has not been solved analytically in arbitrary dimensions has led to intense research into numerical methods for these strongly correlated electron systems. One major goal of this research is to determine the low-temperature phase diagram of this model, particularly in two-dimensions. Approximate numerical treatment of the Hubbard model on finite systems is possible via various methods.

One such method, the Lanczos algorithm, can produce static and dynamic properties of the system. Ground state calculations using this method require the storage of three vectors of the size of the number of states. The number of states scales exponentially with the size of the system, which limits the number of sites in the lattice to about 20 on 21st century hardware. With projector and finite-temperature auxiliary-field Monte Carlo, two statistical methods exist that can obtain certain properties of the system. For low temperatures, convergence problems appear that lead to an exponential computational effort with decreasing temperature due to the so-called fermion sign problem.

The Hubbard model can be studied within dynamical mean-field theory (DMFT). This scheme maps the Hubbard Hamiltonian onto a single-site impurity model, a mapping that is formally exact only in infinite dimensions and in finite dimensions corresponds to the exact treatment of all purely local correlations only. DMFT allows one to compute the local Green's function of the Hubbard model for a given [math]\displaystyle{ U }[/math] and a given temperature. Within DMFT, the evolution of the spectral function can be computed and the appearance of the upper and lower Hubbard bands can be observed as correlations increase.

Simulator

Stacks of heterogeneous 2-dimensional transition metal dichalcogenides (TMD) have been used to simulate geometries in more than one dimension. Tungsten diselenide and tungsten sulfide were stacked. This created a moiré superlattice consisting of hexagonal supercells (repetition units defined by the relationship of the two materials). Each supercell then behaves as though it were a single atom. The distance between supercells is roughly 100x that of the atoms within them. This larger distance drastically reduces electron tunneling across supercells.

They can be used to form Wigner crystals. Electrodes can be attached to regulate an electric field. The electric field controls how many electrons fill each supercell. The number of electrons per supercell effectively determines which "atom" the lattice simulates. One electron/cell behaves like hydrogen, two/cell like helium, etc. As of 2022, supercells with up to eight electrons (oxygen) could be simulated. One result of the simulation showed that the difference between metal and insulator is a continuous function of the electric field strength.

A "backwards" stacking regime allows the creation of a Chern insulator via the anomalous quantum Hall effect (with the edges of the device acting as a conductor while the interior acted as an insulator.) The device functioned at a temperature of 5 Kelvins, far above the temperature at which the effect had first been observed.

See also

• Anderson impurity model
• Bloch's theorem
• Electronic band structure
• Solid-state physics
• Bose–Hubbard model
• t-J model
• Heisenberg model (quantum)
• Dynamical mean-field theory
• Stoner criterion

Further reading

• Hubbard, J. (1963). "Electron Correlations in Narrow Energy Bands". Proceedings of the Royal Society of London 276 (1365): 238–257. doi:10.1098/rspa.1963.0204. Bibcode: 1963RSPSA.276..238H. 
• Bach, V.; Lieb, E. H.; Solovej, J. P. (1994). "Generalized Hartree–Fock Theory and the Hubbard Model". Journal of Statistical Physics 76 (1–2): 3. doi:10.1007/BF02188656. Bibcode: 1994JSP....76....3B. 
• Lieb, E. H. (1995). "The Hubbard Model: Some Rigorous Results and Open Problems". Xi Int. Cong. Mp, Int. Press (?) 1995: cond–mat/9311033. Bibcode: 1993cond.mat.11033L. 
• Gebhard, F. (1997). "Metal–Insulator Transition". The Mott Metal–Insulator Transition: Models and Methods. Springer Tracts in Modern Physics. 137. Springer. pp. 1–48. ISBN 9783540614814. https://books.google.com/books?id=uCPgHgEKnwEC&pg=PA1. 
• Lieb, E. H.; Wu, F. Y. (2003). "The one-dimensional Hubbard model: A reminiscence". Physica A 321 (1): 1–27. doi:10.1016/S0378-4371(02)01785-5. Bibcode: 2003PhyA..321....1L. 
• Arovas, Daniel P.; Berg, Erez; Kivelson, Steven; Rahgu, Sri (2022). "The Hubbard Model". Annual Review of Condensed Matter Physics 13: 239–274. doi:10.1146/annurev-conmatphys-031620-102024. Bibcode: 2022ARCMP..13..239A. 
• Qin, Mingpu; Schäfer, Thomas; Andergassen, Sabine; Corboz, Philippe; Gull, Emanuel (2022). "The Hubbard Model: A Computational Perspective". Annual Review of Condensed Matter Physics 13: 275–302. doi:10.1146/annurev-conmatphys-090921-033948. Bibcode: 2022ARCMP..13..275Q.