Physics:Ultimate tensile strength
Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or [math]\displaystyle{ F_\text{tu} }[/math] in notation)[1] is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials, the ultimate tensile strength is close to the yield point, whereas in ductile materials, the ultimate tensile strength can be higher.
The ultimate tensile strength is usually found by performing a tensile test and recording the engineering stress versus strain. The highest point of the stress–strain curve is the ultimate tensile strength and has units of stress. The equivalent point for the case of compression, instead of tension, is called the compressive strength.
Tensile strengths are rarely of any consequence in the design of ductile members, but they are important with brittle members. They are tabulated for common materials such as alloys, composite materials, ceramics, plastics, and wood.
Definition
The ultimate tensile strength of a material is an intensive property; therefore its value does not depend on the size of the test specimen. However, depending on the material, it may be dependent on other factors, such as the preparation of the specimen, the presence or otherwise of surface defects, and the temperature of the test environment and material.
Some materials break very sharply, without plastic deformation, in what is called a brittle failure. Others, which are more ductile, including most metals, experience some plastic deformation and possibly necking before fracture.
Tensile strength is defined as a stress, which is measured as force per unit area. For some non-homogeneous materials (or for assembled components) it can be reported just as a force or as a force per unit width. In the International System of Units (SI), the unit is the pascal (Pa) (or a multiple thereof, often megapascals (MPa), using the SI prefix mega); or, equivalently to pascals, newtons per square metre (N/m2). A United States customary unit is pounds per square inch (lb/in2 or psi). Kilopounds per square inch (ksi, or sometimes kpsi) is equal to 1000 psi, and is commonly used in the United States, when measuring tensile strengths.
Ductile materials
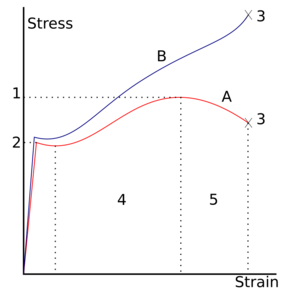
- 1: Ultimate strength
- 2: Yield strength (yield point)
- 3: Rupture
- 4: Strain hardening region
- 5: Necking region
- A: Apparent stress (F/A0)
- B: Actual stress (F/A)
Many materials can display linear elastic behavior, defined by a linear stress–strain relationship, as shown in figure 1 up to point 3. The elastic behavior of materials often extends into a non-linear region, represented in figure 1 by point 2 (the "yield strength"), up to which deformations are completely recoverable upon removal of the load; that is, a specimen loaded elastically in tension will elongate, but will return to its original shape and size when unloaded. Beyond this elastic region, for ductile materials, such as steel, deformations are plastic. A plastically deformed specimen does not completely return to its original size and shape when unloaded. For many applications, plastic deformation is unacceptable, and is used as the design limitation.
After the yield point, ductile metals undergo a period of strain hardening, in which the stress increases again with increasing strain, and they begin to neck, as the cross-sectional area of the specimen decreases due to plastic flow. In a sufficiently ductile material, when necking becomes substantial, it causes a reversal of the engineering stress–strain curve (curve A, figure 2); this is because the engineering stress is calculated assuming the original cross-sectional area before necking. The reversal point is the maximum stress on the engineering stress–strain curve, and the engineering stress coordinate of this point is the ultimate tensile strength, given by point 1.
Ultimate tensile strength is not used in the design of ductile static members because design practices dictate the use of the yield stress. It is, however, used for quality control, because of the ease of testing. It is also used to roughly determine material types for unknown samples.[2]
The ultimate tensile strength is a common engineering parameter to design members made of brittle material because such materials have no yield point.[2]
Testing
Typically, the testing involves taking a small sample with a fixed cross-sectional area, and then pulling it with a tensometer at a constant strain (change in gauge length divided by initial gauge length) rate until the sample breaks.
When testing some metals, indentation hardness correlates linearly with tensile strength. This important relation permits economically important nondestructive testing of bulk metal deliveries with lightweight, even portable equipment, such as hand-held Rockwell hardness testers.[3] This practical correlation helps quality assurance in metalworking industries to extend well beyond the laboratory and universal testing machines.
Typical tensile strengths
| Material | Yield strength (MPa) |
Ultimate tensile strength (MPa) |
Density (g/cm3) |
|---|---|---|---|
| Steel, structural ASTM A36 steel | 250 | 400–550 | 7.8 |
| Steel, 1090 mild | 247 | 841 | 7.58 |
| Chromium-vanadium steel AISI 6150 | 620 | 940 | 7.8 |
| Steel, 2800 Maraging steel[4] | 2,617 | 2,693 | 8.00 |
| Steel, AerMet 340[5] | 2,160 | 2,430 | 7.86 |
| Steel, Sandvik Sanicro 36Mo logging cable precision wire[6] | 1,758 | 2,070 | 8.00 |
| Steel, AISI 4130, water quenched 855 °C (1,570 °F), 480 °C (900 °F) temper[7] |
951 | 1,110 | 7.85 |
| Steel, API 5L X65[8] | 448 | 531 | 7.8 |
| Steel, high strength alloy ASTM A514 | 690 | 760 | 7.8 |
| Acrylic, clear cast sheet (PMMA)[9] | 72 | 87[10] | 1.16 |
| Acrylonitrile butadiene styrene (ABS) [11] | 43 | 43 | 0.9–1.53 |
| High-density polyethylene (HDPE) | 26–33 | 37 | 0.85 |
| Polypropylene | 12–43 | 19.7–80 | 0.91 |
| Steel, stainless AISI 302[12] | 275 | 620 | 7.86 |
| Cast iron 4.5% C, ASTM A-48 | 130 | 200 | 7.3 |
| "Liquidmetal" alloy[citation needed] | 1,723 | 550–1,600 | 6.1 |
| Beryllium[13] 99.9% Be | 345 | 448 | 1.84 |
| Aluminium alloy[14] 2014-T6 | 414 | 483 | 2.8 |
| Polyester resin (unreinforced)[15] | 55 | 55 | |
| Polyester and chopped strand mat laminate 30% E-glass[15] | 100 | 100 | |
| S-Glass epoxy composite[16] | 2,358 | 2,358 | |
| Aluminium alloy 6061-T6 | 241 | 300 | 2.7 |
| Copper 99.9% Cu | 70 | 220[citation needed] | 8.92 |
| Cupronickel 10% Ni, 1.6% Fe, 1% Mn, balance Cu | 130 | 350 | 8.94 |
| Brass | 200 + | 500 | 8.73 |
| Tungsten | 941 | 1,510 | 19.25 |
| Glass | 33[17] | 2.53 | |
| E-Glass | N/A | 1,500 for laminates, 3,450 for fibers alone |
2.57 |
| S-Glass | N/A | 4,710 | 2.48 |
| Basalt fiber[18] | N/A | 4,840 | 2.7 |
| Marble | N/A | 15 | 2.6 |
| Concrete | N/A | 2–5 | 2.7 |
| Carbon fiber | N/A | 1,600 for laminates, 4,137 for fibers alone |
1.75 |
| Carbon fiber (Toray T1100G)[19] (the strongest human-made fibres) |
7,000 fibre alone | 1.79 | |
| Human hair | 140–160 | 200–250[20] | |
| Bamboo fiber | 350–500 | 0.4–0.8 | |
| Spider silk (see note below) | 1,000 | 1.3 | |
| Spider silk, Darwin's bark spider[21] | 1,652 | ||
| Silkworm silk | 500 | 1.3 | |
| Aramid (Kevlar or Twaron) | 3,620 | 3,757 | 1.44 |
| UHMWPE[22] | 24 | 52 | 0.97 |
| UHMWPE fibers[23][24] (Dyneema or Spectra) | 2,300–3,500 | 0.97 | |
| Vectran | 2,850–3,340 | 1.4 | |
| Polybenzoxazole (Zylon)[25] | 2,700 | 5,800 | 1.56 |
| Wood, pine (parallel to grain) | 40 | ||
| Bone (limb) | 104–121 | 130 | 1.6 |
| Nylon, molded, 6PLA/6M [26] | 75-85 | 1.15 | |
| Nylon fiber, drawn[27] | 900[28] | 1.13 | |
| Epoxy adhesive | N/A | 12–30[29] | N/A |
| Rubber | N/A | 16 | |
| Boron | N/A | 3,100 | 2.46 |
| Silicon, monocrystalline (m-Si) | N/A | 7,000 | 2.33 |
| Ultra-pure silica glass fiber-optic strands[30] | 4,100 | ||
| Sapphire (Al2O3) | 400 at 25 °C, 275 at 500 °C, 345 at 1,000 °C |
1,900 | 3.9–4.1 |
| Boron nitride nanotube | N/A | 33,000 | 2.62[31] |
| Diamond | 1,600 | 2,800 ~80–90 GPa at microscale[32] |
3.5 |
| Graphene | N/A | intrinsic 130,000;[33] engineering 50,000–60,000[34] |
1.0 |
| First carbon nanotube ropes | ? | 3,600 | 1.3 |
| Carbon nanotube (see note below) | N/A | 11,000–63,000 | 0.037–1.34 |
| Carbon nanotube composites | N/A | 1,200[35] | N/A |
| High-strength carbon nanotube film | N/A | 9,600[36] | N/A |
| Iron (pure mono-crystal) | 3 | 7.874 | |
| Limpet Patella vulgata teeth (goethite whisker nanocomposite) | 4,900 3,000–6,500[37] |
- ^a Many of the values depend on manufacturing process and purity or composition.
- ^b Multiwalled carbon nanotubes have the highest tensile strength of any material yet measured, with one measurement of 63 GPa, still well below one theoretical value of 300 GPa.[38] The first nanotube ropes (20 mm in length) whose tensile strength was published (in 2000) had a strength of 3.6 GPa.[39] The density depends on the manufacturing method, and the lowest value is 0.037 or 0.55 (solid).[40]
- ^c The strength of spider silk is highly variable. It depends on many factors including kind of silk (Every spider can produce several for sundry purposes.), species, age of silk, temperature, humidity, swiftness at which stress is applied during testing, length stress is applied, and way the silk is gathered (forced silking or natural spinning).[41] The value shown in the table, 1,000 MPa, is roughly representative of the results from a few studies involving several different species of spider however specific results varied greatly.[42]
- ^d Human hair strength varies by ethnicity and chemical treatments.
Typical properties of annealed elements
| Element | Young's modulus (GPa) |
Yield strength (MPa) |
Ultimate strength (MPa) |
|---|---|---|---|
| Silicon | 107 | 5,000–9,000 | |
| Tungsten | 411 | 550 | 550–620 |
| Iron | 211 | 80–100 | 350 |
| Titanium | 120 | 100–225 | 246–370 |
| Copper | 130 | 117 | 210 |
| Tantalum | 186 | 180 | 200 |
| Tin | 47 | 9–14 | 15–200 |
| Zinc | 85–105 | 200–400 | 200–400 |
| Nickel | 170 | 140–350 | 140–195 |
| Silver | 83 | 170 | |
| Gold | 79 | 100 | |
| Aluminium | 70 | 15–20 | 40–50 |
| Lead | 16 | 12 |
See also
References
- ↑ "Generic MMPDS Mechanical Properties Table". 6 December 2014. http://www.stressebook.com/mmpds-mechanical-properties-table/.
- ↑ 2.0 2.1 "Tensile Properties". http://www.ndt-ed.org/EducationResources/CommunityCollege/Materials/Mechanical/Tensile.htm.
- ↑ E.J. Pavlina and C.J. Van Tyne, "Correlation of Yield Strength and Tensile Strength with Hardness for Steels", Journal of Materials Engineering and Performance, 17:6 (December 2008)
- ↑ "MatWeb – The Online Materials Information Resource". http://www.matweb.com/search/DataSheet.aspx?MatGUID=de22e04486ff4598a26027abc48e6382.
- ↑ "MatWeb – The Online Materials Information Resource". http://www.matweb.com/search/DataSheet.aspx?MatGUID=64583c8ce6724989a11e1ef598d3273d.
- ↑ "MatWeb – The Online Materials Information Resource". http://www.matweb.com/search/DataSheet.aspx?MatGUID=c140b20b165941c7a948e782eeced4ea.
- ↑ "MatWeb – The Online Materials Information Resource". http://www.matweb.com/search/datasheet.aspx?MatGUID=722e053100354c02a6d450d5d7646d82.
- ↑ "USStubular.com". http://www.usstubular.com/products/seamslp.htm.
- ↑ [1] IAPD Typical Properties of Acrylics
- ↑ strictly speaking this figure is the flexural strength (or modulus of rupture), which is a more appropriate measure for brittle materials than "ultimate strength."
- ↑ https://www.matweb.com/search/DataSheet.aspx?MatGUID=eb7a78f5948d481c9493a67f0d089646
- ↑ "Stainless Steel - Grade 302 (UNS S30200)" (in en). 2013-02-25. https://www.azom.com/article.aspx?ArticleID=8197.
- ↑ "MatWeb – The Online Materials Information Resource". http://www.matweb.com/search/datasheet.aspx?matguid=9878e52807a249b8a6f3a6e4c179a732&ckck=1.
- ↑ "MatWeb – The Online Materials Information Resource". http://www.matweb.com/search/DataSheet.aspx?MatGUID=e5de9f1161d34f71a34ae016723d097f.
- ↑ 15.0 15.1 "Guide to Glass Reinforced Plastic (fibreglass) – East Coast Fibreglass Supplies". http://www.ecfibreglasssupplies.co.uk/t-GlassReinforcedPlastics.aspx.
- ↑ "Properties of Carbon Fiber Tubes". http://www.carbonfibertubeshop.com/tube%20properties.html.
- ↑ "Soda-Lime (Float) Glass Material Properties :: MakeItFrom.com". http://www.makeitfrom.com/data/?material=Soda_Lime_Glass&type=Mechanical.
- ↑ "Basalt Continuous Fibers". http://www.albarrie.com/techfabrics/continuousfiber.aspx.
- ↑ "Toray Properties Document". https://www.toraycma.com/file_viewer.php?id=5136.
- ↑ "Tensile Testing Hair". instron.us. http://www.instron.us/en-us/testing-solutions/by-test-type/tension/testing-hair.
- ↑ Agnarsson, I; Kuntner, M; Blackledge, TA (2010). "Bioprospecting Finds the Toughest Biological Material: Extraordinary Silk from a Giant Riverine Orb Spider". PLOS ONE 5 (9): e11234. doi:10.1371/journal.pone.0011234. PMID 20856804. Bibcode: 2010PLoSO...511234A.
- ↑ Oral, E; Christensen, SD; Malhi, AS; Wannomae, KK; Muratoglu, OK (2006). "PubMed Central, Table 3". J Arthroplasty 21 (4): 580–91. doi:10.1016/j.arth.2005.07.009. PMID 16781413.
- ↑ "Tensile and creep properties of ultra high molecular weight PE fibres". http://www-lgm2b.iut.u-bordeaux1.fr/publi/PE%20fibre.pdf.
- ↑ "Mechanical Properties Data". http://www.mse.mtu.edu/~drjohn/my4150/props.html.
- ↑ "MatWeb – The Online Materials Information Resource". http://www.matweb.com/search/datasheet.aspx?matguid=1a5f4985c8fb449da6edaec7813acf70&ckck=1.
- ↑ "Material Properties Chart". https://advancednylons.co.za/Materialproperties.pdf.
- ↑ "Nylon Fibers". University of Tennessee. http://www.engr.utk.edu/mse/pages/Textiles/Nylon%20fibers.htm.
- ↑ "Comparing aramids". Teijin Aramid. http://www.teijinaramid.com/aramids/comparing-aramids/.
- ↑ "Uhu endfest 300 epoxy: Strength over setting temperature". http://www.stirlingshop.de/epages/61267352.sf/en_GB/?ObjectPath=/Shops/61267352/Products/0001.
- ↑ "Fols.org". http://www.fols.org/fols_library/white_papers/documents/Fiber%20Myths%20White%20Paper%20final.pdf.
- ↑ "What is the density of Hydrogenated Boron Nitride Nanotubes (H-BNNT)?". http://space.stackexchange.com/questions/14883/what-is-the-density-of-hydrogenated-boron-nitride-nanotubes-h-bnnt.
- ↑ Dang, Chaoqun (January 1, 2021). "Achieving large uniform tensile elasticity in microfabricated diamond". Science 371 (6524): 76–78. doi:10.1126/science.abc4174. PMID 33384375. Bibcode: 2021Sci...371...76D.
- ↑ Lee, C. (2008). "Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene". Science 321 (5887): 385–8. doi:10.1126/science.1157996. PMID 18635798. Bibcode: 2008Sci...321..385L. http://www.sciencemag.org/cgi/content/abstract/321/5887/385.
- Phil Schewe (July 28, 2008). "World's Strongest Material". Inside Science News Service (American Institute of Physics). http://www.aip.org/isns/reports/2008/027.html.
- ↑ Cao, K. (2020). "Elastic straining of free-standing monolayer graphene". Nature Communications 11 (284): 284. doi:10.1038/s41467-019-14130-0. PMID 31941941. Bibcode: 2020NatCo..11..284C.
- ↑ IOP.org Z. Wang, P. Ciselli and T. Peijs, Nanotechnology 18, 455709, 2007.
- ↑ Xu, Wei; Chen, Yun; Zhan, Hang; Nong Wang, Jian (2016). "High-Strength Carbon Nanotube Film from Improving Alignment and Densification". Nano Letters 16 (2): 946–952. doi:10.1021/acs.nanolett.5b03863. PMID 26757031. Bibcode: 2016NanoL..16..946X.
- ↑ Barber, A. H.; Lu, D.; Pugno, N. M. (2015). "Extreme strength observed in limpet teeth". Journal of the Royal Society Interface 12 (105): 105. doi:10.1098/rsif.2014.1326. PMID 25694539.
- ↑ Yu, Min-Feng; Lourie, O; Dyer, MJ; Moloni, K; Kelly, TF; Ruoff, RS (2000). "Strength and Breaking Mechanism of Multiwalled Carbon Nanotubes Under Tensile Load". Science 287 (5453): 637–640. doi:10.1126/science.287.5453.637. PMID 10649994. Bibcode: 2000Sci...287..637Y.
- ↑ Li, F.; Cheng, H. M.; Bai, S.; Su, G.; Dresselhaus, M. S. (2000). "Tensile strength of single-walled carbon nanotubes directly measured from their macroscopic ropes". Applied Physics Letters 77 (20): 3161. doi:10.1063/1.1324984. Bibcode: 2000ApPhL..77.3161L.
- ↑ K.Hata. "From Highly Efficient Impurity-Free CNT Synthesis to DWNT forests, CNTsolids and Super-Capacitors". http://nanocarbon.jp/english/research/image/review.pdf.
- ↑ Elices. "Finding Inspiration in Argiope Trifasciata Spider Silk Fibers". JOM. http://www.tms.org/pubs/journals/JOM/0502/Elices-0502.html.
- ↑ Blackledge (2005). "Quasistatic and continuous dynamic characterization of the mechanical properties of silk from the cobweb of the black widow spider Latrodectus hesperus". Journal of Experimental Biology (The Company of Biologists) 208 (10): 1937–1949. doi:10.1242/jeb.01597. PMID 15879074. http://jeb.biologists.org/cgi/content/full/208/10/1937. Retrieved 2009-01-23.
- ↑ A.M. Howatson, P. G. Lund, and J. D. Todd, Engineering Tables and Data, p. 41
Further reading
- Giancoli, Douglas, Physics for Scientists & Engineers Third Edition (2000). Upper Saddle River: Prentice Hall.
- Köhler, T.; Vollrath, F. (1995). "Thread biomechanics in the two orb-weaving spiders Araneus diadematus (Araneae, Araneidae) and Uloboris walckenaerius (Araneae, Uloboridae)". Journal of Experimental Zoology 271: 1–17. doi:10.1002/jez.1402710102.
- T Follett, Life without metals
- Min-Feng, Yu; Lourie, O; Dyer, MJ; Moloni, K; Kelly, TF; Ruoff, RS (2000). "Strength and Breaking Mechanism of Multiwalled Carbon Nanotubes Under Tensile Load". Science 287 (5453): 637–640. doi:10.1126/science.287.5453.637. PMID 10649994. Bibcode: 2000Sci...287..637Y. http://www.bimat.org/assets/pdf/00_287yu.pdf.
- George E. Dieter, Mechanical Metallurgy (1988). McGraw-Hill, UK
 |






