Physics:Trouton–Noble experiment

A circular capacitor B, 7.7 cm in diameter, built from multiple layers of mica and tinfoil, was fitted into a smooth spherical celluloid ball D that was covered with conductive paint, and which was suspended by a fine phosphor-bronze wire 37 cm long within a grounded tube. The wire was connected to one electrode of a Wimshurst machine which kept alternate plates of the capacitor charged to 3000 volts. The opposite plates of the capacitor as well as the celluloid ball were kept at ground voltage by means of a platinum wire that dipped into a sulfuric acid bath that not only served as a conductive electrode, but also damped oscillations and acted as a desiccant. A mirror attached to the capacitor was viewed through a telescope and allowed fine changes in orientation to be viewed.

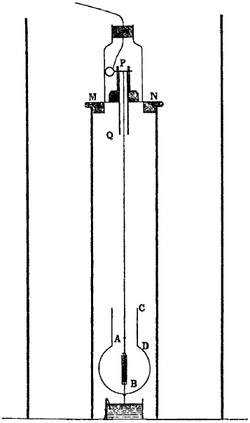
The Trouton–Noble experiment was an attempt to detect motion of the Earth through the luminiferous aether, and was conducted in 1901–1903 by Frederick Thomas Trouton and H. R. Noble. It was based on a suggestion by George FitzGerald that a charged parallel-plate capacitor moving through the aether should orient itself perpendicular to the motion. Like the earlier Michelson–Morley experiment, Trouton and Noble obtained a null result: no motion relative to the aether could be detected. This null result was reproduced, with increasing sensitivity, by Rudolf Tomaschek (1925, 1926), Chase (1926, 1927) and Hayden in 1994. Such experimental results are now seen, consistent with special relativity, to reflect the validity of the principle of relativity and the absence of any absolute rest frame (or aether). The experiment is a test of special relativity.

The Trouton–Noble experiment is also related to thought experiments such as the "Trouton–Noble paradox," and the "right-angle lever" or "Lewis–Tolman paradox". Several solutions have been proposed to solve this kind of paradox, all of them in agreement with special relativity.

Trouton–Noble experiment

In the experiment, a suspended parallel-plate capacitor is held by a fine torsion fiber and is charged. If the aether theory were correct, the change in Maxwell's equations due to the Earth's motion through the aether would lead to a torque causing the plates to align perpendicular to the motion. This is given by:

[math]\displaystyle{ \tau=-E'\frac{v^{2}}{c^{2}}\sin2\alpha' }[/math]

where [math]\displaystyle{ \tau }[/math] is the torque, [math]\displaystyle{ E }[/math] the energy of the condenser, [math]\displaystyle{ \alpha }[/math] the angle between the normal of the plate and the velocity.

On the other hand, the assertion of special relativity that Maxwell's equations are invariant for all frames of reference moving at constant velocities would predict no torque (a null result). Thus, unless the aether were somehow fixed relative to the Earth, the experiment is a test of which of these two descriptions is more accurate. Its null result thus confirms Lorentz invariance of special relativity.

However, while the negative experimental outcome can easily be explained in the rest frame of the device, the explanation from the viewpoint of a non-co-moving frame (concerning the question, whether the same torque should arise as in the "aether frame" described above, or whether no torque arises at all) is much more difficult and is called "Trouton–Noble paradox," which can be solved in several ways (see Solutions below).

Right-angle lever paradox

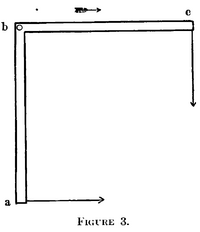
The Trouton–Noble paradox is essentially equivalent to a thought experiment called the right angle lever paradox, first discussed by Gilbert Newton Lewis and Richard Chase Tolman in 1909. Suppose a right-angle lever with endpoints abc. In its rest frame, the forces [math]\displaystyle{ f_y }[/math] towards ba and [math]\displaystyle{ f_x }[/math] towards bc must be equal to obtain equilibrium, thus no torque is given by the law of the lever:

[math]\displaystyle{ \tau'=L_{0}\left(f'_{x}-f'_{y}\right)=0 }[/math]

where [math]\displaystyle{ \tau }[/math] is the torque, and [math]\displaystyle{ L_0 }[/math] the rest length of one lever arm. However, due to length contraction, ba is longer than bc in a non-co-moving system, thus the law of the lever gives:

[math]\displaystyle{ \tau=f_{x}\cdot L_{0}-f_{y}\cdot L_{0}\sqrt{1-\frac{v^{2}}{c^{2}}}=L_{0}\left(f_{x}-f_{y}\sqrt{1-\frac{v^{2}}{c^{2}}}\right) }[/math]

It can be seen that the torque is not zero, which apparently would cause the lever to rotate in the non-co-moving frame. Since no rotation is observed, Lewis and Tolman thus concluded that no torque exists, therefore:

[math]\displaystyle{ \frac{f_{x}}{f_{y}}=\sqrt{1-\frac{v^{2}}{c^{2}}} }[/math]

However, as shown by Max von Laue (1911), this is in contradiction with the relativistic expressions of force,

[math]\displaystyle{ f_{x}=f'_{x},\ f_{y}=f'_{y}\cdot\sqrt{1-\frac{v^{2}}{c^{2}}} }[/math]

which gives

[math]\displaystyle{ \frac{f_{x}}{f_{y}}=\frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}} }[/math]

When applied to the law of the lever, the following torque is produced:

[math]\displaystyle{ \tau=-L_{0}\cdot f'_{x}\cdot\frac{v^{2}}{c^{2}} }[/math]

Which is principally the same problem as in the Trouton–Noble paradox.

Solutions

The detailed relativistic analysis of both the Trouton–Noble paradox and the right-angle lever paradox requires care to correctly reconcile, for example, the effects seen by observers in different frames of reference, but ultimately all such theoretical descriptions are shown to give the same result. In both cases an apparent net torque on an object (when viewed from a certain frame of reference) does not result in any rotation of the object, and in both cases this is explained by correctly accounting, in the relativistic way, for the transformation of all the relevant forces, momenta and the accelerations produced by them. The early history of descriptions of this experiment is reviewed by Janssen (1995).

Laue current

The first solution of the Trouton–Noble paradox was given by Hendrik Lorentz (1904). His result is based on the assumption that the torque and momentum due to electrostatic forces are compensated by the torque and momentum due to molecular forces. However, there is no known mechanism for how a Lorentz transformation could produce such molecular forces. In addition, if two point charges are connected by a flexible string, no molecular force could produce a turning moment.

This was further elaborated by Max von Laue (1911), who gave the standard solution for these kind of paradoxes. It was based on the so-called "inertia of energy" in its general formulation by Max Planck. According to Laue, an energy current connected with a certain momentum ("Laue current") is produced in moving bodies by elastic stresses. The resulting mechanical torque in the case of the Trouton–Noble experiment amounts to:

[math]\displaystyle{ \tau=E'\frac{v^{2}}{c^{2}}\sin2\alpha' }[/math]

and in the right-angle lever:

[math]\displaystyle{ \tau=L_{0}\cdot f'_{x}\cdot\frac{v^{2}}{c^{2}} }[/math]

which exactly compensates the electromagnetic torque mentioned above, thus no rotation occurs on both cases. Or in other words: The electromagnetic torque is actually necessary for the uniform motion of a body, i.e., to hinder the body to rotate due to the mechanical torque caused by elastic stresses.

Since then, many papers appeared which elaborated on Laue's current, providing some modifications or re-interpretations, and included different variants of "hidden" momentum.

Force and acceleration

A solution without compensating forces or redefinitions of force and equilibrium was published by Richard C. Tolman and Paul Sophus Epstein in 1911. They applied the notion of a relativistic mass that was different in the longitudinal direction and the transverse direction so that force and acceleration do not always have the same direction. The role played by the concept of force in relativity is very different from that of Newtonian mechanics. A similar conclusion was reached by Franklin (2006), using invariant mass that did not change with direction, but using the fact that the direction of relativistic acceleration is different from the direction of relativistic force.

Epstein imagined a massless rod with endpoints OM, which is mounted at point O, and a particle with rest mass m is mounted at M (see [1]). The rod forms the angle [math]\displaystyle{ \tan\alpha' }[/math] with the y'-axis. Now a force [math]\displaystyle{ f' }[/math] towards O is applied at M, and equilibrium in its rest frame is achieved when [math]\displaystyle{ \tfrac{f'_{x}}{f'_{y}}=\tan\alpha' }[/math]. As already shown above, these forces have the form in a non-co-moving frame:

[math]\displaystyle{ f_{x}=f'_{x},\ f_{y}=f'_{y}\cdot\sqrt{1-\frac{v^{2}}{c^{2}}},\ \tan\alpha=\tan\alpha'\sqrt{1-\frac{v^{2}}{c^{2}}} }[/math]

Thus [math]\displaystyle{ \frac{f_{x}}{f_{y}}=\frac{\tan\alpha}{1-\frac{v^{2}}{c^{2}}} }[/math].

So the resultant force does not directly point from O to M. Does this lead to a rotation of the rod? No, because Epstein now considered the accelerations caused by the two forces. He used the concept of a relativistic mass that was different in the longitudinal direction and the transverse direction such that

[math]\displaystyle{ m_{\rm long.}={m_0\gamma^3},\ m_{\rm tr.}=m_0\gamma,\quad {\rm where}\quad \gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} }[/math].

The relativistic expressions in the case, where a mass m is accelerated by these two forces in the longitudinal and transverse direction, are

[math]\displaystyle{ a_{x}=\frac{f_{x}}{m\gamma^{3}},\ a_{y}=\frac{f_{y}}{m\gamma} }[/math].

Thus [math]\displaystyle{ \frac{a_{x}}{a_{y}}=\tan\alpha }[/math].

Franklin used the relativistic connection between force and acceleration,

[math]\displaystyle{ \frac{d\bf p}{dt}=m\frac{d}{dt}({\bf v}\gamma)=m\gamma^3[{\bf a}+{\bf v\times(v\times a)}]. }[/math]

Using this relation between relativistic force and acceleration, it can be shown that no rotation occurs in this system. Similar considerations are also to be applied to the right-angle lever and Trouton–Noble paradox. So the paradoxes are resolved, because the two accelerations (as vectors) point to the center of gravity of the system, although the two forces do not.

See also

• History of special relativity

Further reading

History

• Michel Janssen, "A comparison between Lorentz's ether theory and special relativity in the light of the experiments of Trouton and Noble, Ph.D. thesis (1995). Online: TOC, pref., intro-I, 1, 2, intro-II, 3, 4, refs.
• Janssen, Michel H. P. (2008), "Drawing the line between kinematics and dynamics in special relativity", Symposium on Time and Relativity 40 (1): 1–76, doi:10.1016/j.shpsb.2008.06.004, Bibcode: 2009SHPMP..40...26J, http://philsci-archive.pitt.edu/3895/ 

Textbooks

• Tolman, R.C. (1917), "The Right-Angled Lever", The theory of relativity of motion, Berkeley: University of California press, pp. 539–776, 152–153, https://archive.org/details/theoryrelativmot00tolmrich 
• Pauli, Wolfgang (1981). "Applications to special cases. Trouton's and Noble's experiment". Theory of Relativity. New York: Dover. pp. 127–130. ISBN 978-0-486-64152-2. https://archive.org/details/theoryrelativity00paul. 
• Panofsky, Wolfgang; Phillips, Melba (2005). Classical electricity and magnetism. Dover. pp. 274, 349. ISBN 978-0-486-43924-2. https://archive.org/details/classicalelectri00pano_298. 
• Jackson, John D. (1998). Classical Electrodynamics (3rd ed.). Wiley. ISBN 978-0-471-30932-1. https://archive.org/details/classicalelectro0000jack_e8g9. 
• Franklin, J. (2017). Classical Electromagnetism (2nd ed.). Dover. pp. 467–468. ISBN 978-0-486-81371-4. 

American Journal of Physics

• Gamba, A. (1967). "Physical Quantities in Different Reference Systems According to Relativity". American Journal of Physics 35 (2): 83–89. doi:10.1119/1.1973974. Bibcode: 1967AmJPh..35...83G. 
• Butler, J. W. (1968). "On the Trouton-Noble Experiment". American Journal of Physics 36 (11): 936–941. doi:10.1119/1.1974358. Bibcode: 1968AmJPh..36..936B. 
• Aranoff, S. (1969). "Torques and Angular Momentum on a System at Equilibrium in Special Relativity". American Journal of Physics 37 (4): 453–454. doi:10.1119/1.1975612. Bibcode: 1969AmJPh..37..453A. 
• Furry, W. H. (1969). "Examples of Momentum Distributions in the Electromagnetic Field and in Matter". American Journal of Physics 37 (6): 621–636. doi:10.1119/1.1975729. Bibcode: 1969AmJPh..37..621F. 
• Butler, J. W. (1969). "A Proposed Electromagnetic Momentum-Energy 4-Vector for Charged Bodies". American Journal of Physics 37 (12): 1258–1272. doi:10.1119/1.1975297. Bibcode: 1969AmJPh..37.1258B. 
• Butler, J. W. (1970). "The Lewis-Tolman Lever Paradox". American Journal of Physics 38 (3): 360–368. doi:10.1119/1.1976326. Bibcode: 1970AmJPh..38..360B. 
• Rohrlich, F. (1970). "Electromagnetic Momentum, Energy, and Mass". American Journal of Physics 38 (11): 1310–1316. doi:10.1119/1.1976082. Bibcode: 1970AmJPh..38.1310R. 
• Sears, Francis W. (1972). "Another Relativistic Paradox". American Journal of Physics 40 (5): 771–773. doi:10.1119/1.1986643. Bibcode: 1972AmJPh..40..771S. 
• Aranoff, S. (1973). "More on the Right-Angled Lever at Equilibrium in Special Relativity". American Journal of Physics 41 (9): 1108–1109. doi:10.1119/1.1987485. Bibcode: 1973AmJPh..41.1108A. 
• Nickerson, J. Charles; McAdory, Robert T. (1975). "The Trouton-Noble paradox". American Journal of Physics 43 (7): 615–621. doi:10.1119/1.9761. Bibcode: 1975AmJPh..43..615N. 
• Cavalleri, G.; Grøn, Ø.; Spavieri, G.; Spinelli, G. (1978). "Comment on the article "Right-angle lever paradox" by J. C. Nickerson and R. T. McAdory". American Journal of Physics 46 (1): 108–109. doi:10.1119/1.11106. Bibcode: 1978AmJPh..46..108C. 
• Grøn, Ø. (1978). "Relativistics statics and F. W. Sears". American Journal of Physics 46 (3): 249–250. doi:10.1119/1.11164. Bibcode: 1978AmJPh..46..249G. 
• Holstein, Barry R.; Swift, Arthur R. (1982). "Flexible string in special relativity". American Journal of Physics 50 (10): 887–889. doi:10.1119/1.13002. Bibcode: 1982AmJPh..50..887H. 
• Singal, Ashok K. (1993). "On the "explanation" of the null results of Trouton-Noble experiment". American Journal of Physics 61 (5): 428–433. doi:10.1119/1.17236. Bibcode: 1993AmJPh..61..428S. 
• Teukolsky, Saul A. (1996). "The explanation of the Trouton-Noble experiment revisited". American Journal of Physics 64 (9): 1104–1109. doi:10.1119/1.18329. Bibcode: 1996AmJPh..64.1104T. https://authors.library.caltech.edu/88290/1/1.18329.pdf. 
• Jackson, J. D. (2004). "Torque or no torque? Simple charged particle motion observed in different inertial frames". American Journal of Physics 72 (12): 1484–1487. doi:10.1119/1.1783902. Bibcode: 2004AmJPh..72.1484J. 

European Journal of Physics

• Aguirregabiria, J. M.; Hernandez, A.; Rivas, M. (1982). "A Lewis-Tolman-like paradox". European Journal of Physics 3 (1): 30–33. doi:10.1088/0143-0807/3/1/008. Bibcode: 1982EJPh....3...30A. 
• Franklin, Jerrold (2006). "The lack of rotation in the Trouton Noble experiment". European Journal of Physics 27 (5): 1251–1256. doi:10.1088/0143-0807/27/5/024. Bibcode: 2006EJPh...27.1251F. 
• Franklin, Jerrold (2008). "The lack of rotation in a moving right angle lever". European Journal of Physics 29 (6): N55–N58. doi:10.1088/0143-0807/29/6/N01. Bibcode: 2008EJPh...29...55F. 

Journal of Physics A

• Jefimenko, Oleg D. (1999). "The Trouton-Noble paradox". Journal of Physics A 32 (20): 3755–3762. doi:10.1088/0305-4470/32/20/308. Bibcode: 1999JPhA...32.3755J. 

Nuovo Cimento

• Arzeliès, H. (1965). "Sur le problème relativiste du levier coudé". Il Nuovo Cimento 35 (3): 783–791. doi:10.1007/BF02739341. Bibcode: 1965NCim...35..783A. 
• Rohrlich, F. (1966). "True and apparent transformations, classical electrons, and relativistic thermodynamics". Il Nuovo Cimento B 45 (1): 76–83. doi:10.1007/BF02710587. Bibcode: 1966NCimB..45...76R. 
• Newburgh, R. G. (1969). "The relativistic problem of the right-angled lever: The correctness of the Laue solution". Il Nuovo Cimento B 61 (2): 201–209. doi:10.1007/BF02710928. Bibcode: 1969NCimB..61..201N. 
• Cavalleri, G.; Salgarelli, G. (1969). "Revision of the relativistic dynamics with variable rest mass and application to relativistic thermodynamics". Il Nuovo Cimento A 62 (3): 722–754. doi:10.1007/BF02819595. Bibcode: 1969NCimA..62..722C. 
• Aranoff, S. (1972). "Equilibrium in special relativity". Il Nuovo Cimento B 10 (1): 155–171. doi:10.1007/BF02911417. Bibcode: 1972NCimB..10..155A. http://www.analysis-knowledge.com/Physics/Equilibrium%20in%20Special%20Relativity.pdf. 
• Grøn, Ø. (1973). "The asynchronous formulation of relativistic statics and thermodynamics". Il Nuovo Cimento B 17 (1): 141–165. doi:10.1007/BF02906436. Bibcode: 1973NCimB..17..141G. 
• Pahor, S.; Strnad, J. (1974). "Statics in special relativity". Il Nuovo Cimento B 20 (1): 105–112. doi:10.1007/BF02721111. Bibcode: 1974NCimB..20..105P. 
• Cavalleri, G.; Spavieri, G.; Spinelli, G. (1975). "Ropes and pulleys in special relativity (relativistic statics of threads)". Il Nuovo Cimento B 25 (1): 348–356. doi:10.1007/BF02737685. Bibcode: 1975NCimB..25..348C. 
• Chamorro, A.; Hernández, A. (1978). "A synchronous formulation of relativistic statics". Il Nuovo Cimento B 41 (1): 236–244. doi:10.1007/BF02726555. Bibcode: 1977NCimB..41..236C. 
• Hernández, A.; Rivas, M.; Aguirregabiria, J. M. (1982). "A quantitative analysis of the trouton-noble experiment". Il Nuovo Cimento B 72 (1): 1–12. doi:10.1007/BF02894929. Bibcode: 1982NCimB..72....1H. 
• Ai, Hsiao-Bai (1993). "The historical misconception in relativistic statics". Il Nuovo Cimento B 108 (1): 7–15. doi:10.1007/BF02874335. Bibcode: 1993NCimB.108....7A. 
• Nieves, L.; Rodriguez, M.; Spavieri, G.; Tonni, E. (2001). "An experiment of the Trouton-Noble type as a test of the differential form of Faraday's law". Il Nuovo Cimento B 116 (5): 585. Bibcode: 2001NCimB.116..585N. 
• Spavieri, G.; Gillies, G. T. (2003). "Fundamental tests of electrodynamic theories: Conceptual investigations of the Trouton-Noble and hidden momentum effects". Il Nuovo Cimento B 118 (3): 205. Bibcode: 2003NCimB.118..205S. 

Foundations of Physics

• Prokhovnik, S. J.; Kovács, K. P. (1985). "The application of special relativity to the right-angled lever". Foundations of Physics 15 (2): 167–173. doi:10.1007/BF00735288. Bibcode: 1985FoPh...15..167P. 
• Spavieri, Gianfranco (1990). "Proposal for experiments to detect the missing torque in special relativity". Foundations of Physics Letters 3 (3): 291–302. doi:10.1007/BF00666019. Bibcode: 1990FoPhL...3..291S. 
• Ivezić, Tomislav (2005). "Axiomatic Geometric Formulation of Electromagnetism with Only One Axiom: The Field Equation for the Bivector Field F with an Explanation of the Trouton-Noble Experiment". Foundations of Physics Letters 18 (5): 401–429. doi:10.1007/s10702-005-7533-7. Bibcode: 2005FoPhL..18..401I. 
• Ivezić, Tomislav (2006). "Four-Dimensional Geometric Quantities versus the Usual Three-Dimensional Quantities: The Resolution of Jackson's Paradox". Foundations of Physics 36 (10): 1511–1534. doi:10.1007/s10701-006-9071-y. Bibcode: 2006FoPh...36.1511I. 
• Ivezić, Tomislav (2006). "Trouton Noble Paradox Revisited". Foundations of Physics 37 (4–5): 747–760. doi:10.1007/s10701-007-9116-x. Bibcode: 2007FoPh...37..747I. 

External links

• Kevin Brown, "Trouton-Noble and The Right-Angle Lever at MathPages.
• Michel Janssen, "The Trouton Experiment and E = mc² ," Einstein for Everyone course at UMN (2002).