Picard theorem
In complex analysis, Picard's great theorem and Picard's little theorem are related theorems about the range of an analytic function. They are named after Émile Picard.
The theorems
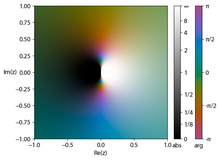
Little Picard Theorem: If a function [math]\displaystyle{ f: \mathbb{C} \to\mathbb{C} }[/math] is entire and non-constant, then the set of values that [math]\displaystyle{ f(z) }[/math] assumes is either the whole complex plane or the plane minus a single point.
Sketch of Proof: Picard's original proof was based on properties of the modular lambda function, usually denoted by [math]\displaystyle{ \lambda }[/math], and which performs, using modern terminology, the holomorphic universal covering of the twice punctured plane by the unit disc. This function is explicitly constructed in the theory of elliptic functions. If [math]\displaystyle{ f }[/math] omits two values, then the composition of [math]\displaystyle{ f }[/math] with the inverse of the modular function maps the plane into the unit disc which implies that [math]\displaystyle{ f }[/math] is constant by Liouville's theorem.
This theorem is a significant strengthening of Liouville's theorem which states that the image of an entire non-constant function must be unbounded. Many different proofs of Picard's theorem were later found and Schottky's theorem is a quantitative version of it. In the case where the values of [math]\displaystyle{ f }[/math] are missing a single point, this point is called a lacunary value of the function.
Great Picard's Theorem: If an analytic function [math]\displaystyle{ f }[/math] has an essential singularity at a point [math]\displaystyle{ w }[/math] , then on any punctured neighborhood of [math]\displaystyle{ w, f(z) }[/math] takes on all possible complex values, with at most a single exception, infinitely often.
This is a substantial strengthening of the Casorati–Weierstrass theorem, which only guarantees that the range of [math]\displaystyle{ f }[/math] is dense in the complex plane. A result of the Great Picard Theorem is that any entire, non-polynomial function attains all possible complex values infinitely often, with at most one exception.
The "single exception" is needed in both theorems, as demonstrated here:
- ez is an entire non-constant function that is never 0,
- [math]\displaystyle{ e^{\frac{1}{z}} }[/math] has an essential singularity at 0, but still never attains 0 as a value.
Proof
Little Picard Theorem
Suppose [math]\displaystyle{ f: \mathbb{C}\to\mathbb{C} }[/math] is an entire function that omits two values [math]\displaystyle{ z_0 }[/math] and [math]\displaystyle{ z_1 }[/math]. By considering [math]\displaystyle{ \frac{f(z)-z_0}{z_1 - z_0} }[/math] we may assume without loss of generality that [math]\displaystyle{ z_0 = 0 }[/math] and [math]\displaystyle{ z_1=1 }[/math].
Because [math]\displaystyle{ \mathbb{C} }[/math] is simply connected and the range of [math]\displaystyle{ f }[/math] omits [math]\displaystyle{ 0 }[/math] , f has a holomorphic logarithm. Let [math]\displaystyle{ g }[/math] be an entire function such that [math]\displaystyle{ f(z)=e^{2\pi ig(z)} }[/math]. Then the range of [math]\displaystyle{ g }[/math] omits all integers. By a similar argument using the quadratic formula, there is an entire function [math]\displaystyle{ h }[/math] such that [math]\displaystyle{ g(z)=\cos(h(z)) }[/math]. Then the range of [math]\displaystyle{ h }[/math] omits all complex numbers of the form [math]\displaystyle{ 2\pi n \pm i \cosh^{-1}(m) }[/math], where [math]\displaystyle{ n }[/math] is an integer and [math]\displaystyle{ m }[/math] is a nonnegative integer.
By Landau's theorem, if [math]\displaystyle{ h'(w) \ne 0 }[/math], then for all [math]\displaystyle{ {R \gt 0} }[/math], the range of [math]\displaystyle{ h }[/math] contains a disk of radius [math]\displaystyle{ |h'(w)| R/72 }[/math]. But from above, any sufficiently large disk contains at least one number that the range of h omits. Therefore [math]\displaystyle{ h'(w)=0 }[/math] for all [math]\displaystyle{ w }[/math]. By the fundamental theorem of calculus, [math]\displaystyle{ h }[/math] is constant, so [math]\displaystyle{ f }[/math] is constant.
Great Picard Theorem
Proof of the Great Picard Theorem
|
|---|
|
Suppose f is an analytic function on the punctured disk of radius r around the point w, and that f omits two values z0 and z1. By considering (f(p + rz) − z0)/(z1 − z0) we may assume without loss of generality that z0 = 0, z1 = 1, w = 0, and r = 1. The function F(z) = f(e−z) is analytic in the right half-plane Re(z) > 0. Because the right half-plane is simply connected, similar to the proof of the Little Picard Theorem, there are analytic functions G and H defined on the right half-plane such that F(z) = e2πiG(z) and G(z) = cos(H(z)). For any w in the right half-plane, the open disk with radius Re(w) around w is contained in the domain of H. By Landau's theorem and the observation about the range of H in the proof of the Little Picard Theorem, there is a constant C > 0 such that |H′(w)| ≤ C / Re(w). Thus, for all real numbers x ≥ 2 and 0 ≤ y ≤ 2π,
where A > 0 is a constant. So |G(x + iy)| ≤ xA. Next, we observe that F(z + 2πi) = F(z) in the right half-plane, which implies that G(z + 2πi) − G(z) is always an integer. Because G is continuous and its domain is connected, the difference G(z + 2πi) − G(z) = k is a constant. In other words, the function G(z) − kz / (2πi) has period 2πi. Thus, there is an analytic function g defined in the punctured disk with radius e−2 around 0 such that G(z) − kz / (2πi) = g(e−z). Using the bound on G above, for all real numbers x ≥ 2 and 0 ≤ y ≤ 2π,
holds, where A′ > A and C′ > 0 are constants. Because of the periodicity, this bound actually holds for all y. Thus, we have a bound |g(z)| ≤ C′(−log|z|)A′ for 0 < |z| < e−2. By Riemann's theorem on removable singularities, g extends to an analytic function in the open disk of radius e−2 around 0. Hence, G(z) − kz / (2πi) is bounded on the half-plane Re(z) ≥ 3. So F(z)e−kz is bounded on the half-plane Re(z) ≥ 3, and f(z)zk is bounded in the punctured disk of radius e−3 around 0. By Riemann's theorem on removable singularities, f(z)zk extends to an analytic function in the open disk of radius e−3 around 0. Therefore, f does not have an essential singularity at 0. Therefore, if the function f has an essential singularity at 0, the range of f in any open disk around 0 omits at most one value. If f takes a value only finitely often, then in a sufficiently small open disk around 0, f omits that value. So f(z) takes all possible complex values, except at most one, infinitely often. |
Generalization and current research
Great Picard's theorem is true in a slightly more general form that also applies to meromorphic functions:
Great Picard's Theorem (meromorphic version): If M is a Riemann surface, w a point on M, P1(C) = C ∪ {∞} denotes the Riemann sphere and f : M\{w} → P1(C) is a holomorphic function with essential singularity at w, then on any open subset of M containing w, the function f(z) attains all but at most two points of P1(C) infinitely often.
Example: The function f(z) = 1/(1 − e1/z) is meromorphic on C* = C - {0}, the complex plane with the origin deleted. It has an essential singularity at z = 0 and attains the value ∞ infinitely often in any neighborhood of 0; however it does not attain the values 0 or 1.
With this generalization, Little Picard Theorem follows from Great Picard Theorem because an entire function is either a polynomial or it has an essential singularity at infinity. As with the little theorem, the (at most two) points that are not attained are lacunary values of the function.
The following conjecture is related to "Great Picard's Theorem":[1]
Conjecture: Let {U1, ..., Un} be a collection of open connected subsets of C that cover the punctured unit disk D \ {0}. Suppose that on each Uj there is an injective holomorphic function fj, such that dfj = dfk on each intersection Uj ∩ Uk. Then the differentials glue together to a meromorphic 1-form on D.
It is clear that the differentials glue together to a holomorphic 1-form g dz on D \ {0}. In the special case where the residue of g at 0 is zero the conjecture follows from the "Great Picard's Theorem".
Notes
References
- Conway, John B. (1978). Functions of One Complex Variable I (2nd ed.). Springer. ISBN 0-387-90328-3.
- Shurman, Jerry. "Sketch of Picard's Theorem". http://people.reed.edu/~jerry/311/picard.pdf. Retrieved 2010-05-18.
 |

