q-Weibull distribution

q-Weibull distribution

Probability density function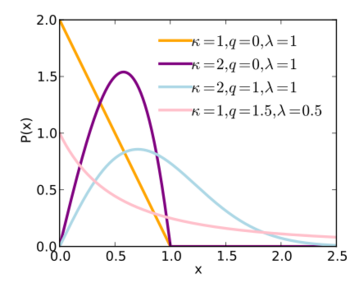
Cumulative distribution function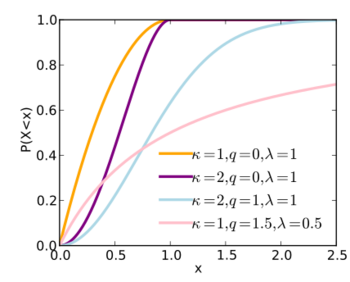
Parameters	[math]\displaystyle{ q \lt 2 }[/math] shape (real) [math]\displaystyle{ \lambda \gt 0 }[/math] rate (real) [math]\displaystyle{ \kappa\gt 0\, }[/math] shape (real)
Support	[math]\displaystyle{ x \in [0; +\infty)\! \text{ for }q \ge 1 }[/math] [math]\displaystyle{ x \in [0; {\lambda \over {(1-q)^{1/\kappa}}}) \text{ for } q\lt 1 }[/math]
PDF	[math]\displaystyle{ \begin{cases} (2-q)\frac{\kappa}{\lambda}\left(\frac{x}{\lambda}\right)^{\kappa-1}e_{q}^{-(x/\lambda)^{\kappa}} & x\geq0\\ 0 & x\lt 0\end{cases} }[/math]
CDF	[math]\displaystyle{ \begin{cases}1- e_{q'}^{-(x/\lambda')^\kappa} & x\geq0\\ 0 & x\lt 0\end{cases} }[/math]
Mean	(see article)

In statistics, the q-Weibull distribution is a probability distribution that generalizes the Weibull distribution and the Lomax distribution (Pareto Type II). It is one example of a Tsallis distribution.

Characterization

Probability density function

The probability density function of a q-Weibull random variable is:

[math]\displaystyle{ f(x;q,\lambda,\kappa) = \begin{cases} (2-q)\frac{\kappa}{\lambda}\left(\frac{x}{\lambda}\right)^{\kappa-1} e_q(-(x/\lambda)^{\kappa})& x\geq0 ,\\ 0 & x\lt 0, \end{cases} }[/math]

where q < 2, [math]\displaystyle{ \kappa }[/math] > 0 are shape parameters and λ > 0 is the scale parameter of the distribution and

[math]\displaystyle{ e_q(x) = \begin{cases} \exp(x) & \text{if }q=1, \\[6pt] [1+(1-q)x]^{1/(1-q)} & \text{if }q \ne 1 \text{ and } 1+(1-q)x \gt 0, \\[6pt] 0^{1/(1-q)} & \text{if }q \ne 1\text{ and }1+(1-q)x \le 0, \\[6pt] \end{cases} }[/math]

is the q-exponential

Cumulative distribution function

The cumulative distribution function of a q-Weibull random variable is:

[math]\displaystyle{ \begin{cases}1- e_{q'}^{-(x/\lambda')^\kappa} & x\geq0\\ 0 & x\lt 0\end{cases} }[/math]

where

[math]\displaystyle{ \lambda' = {\lambda \over (2-q)^{1 \over \kappa}} }[/math]

[math]\displaystyle{ q' = {1 \over (2-q)} }[/math]

Mean

The mean of the q-Weibull distribution is

[math]\displaystyle{ \mu(q,\kappa,\lambda) = \begin{cases} \lambda\,\left(2+\frac{1}{1-q}+\frac{1}{\kappa}\right)(1-q)^{-\frac{1}{\kappa}}\,B\left[1+\frac{1}{\kappa},2+\frac{1}{1-q}\right]& q\lt 1 \\ \lambda\,\Gamma(1+\frac{1}{\kappa}) & q=1\\ \lambda\,(2 - q) (q-1)^{-\frac{1+\kappa}{\kappa}}\,B\left[1+\frac{1}{\kappa}, -\left(1+\frac{1}{q-1}+\frac{1}{\kappa}\right)\right] & 1\lt q\lt 1+\frac{1+2\kappa}{1+\kappa}\\ \infty & 1+\frac{\kappa}{\kappa+1}\le q\lt 2 \end{cases} }[/math]

where [math]\displaystyle{ B() }[/math] is the Beta function and [math]\displaystyle{ \Gamma() }[/math] is the Gamma function. The expression for the mean is a continuous function of q over the range of definition for which it is finite.

Relationship to other distributions

The q-Weibull is equivalent to the Weibull distribution when q = 1 and equivalent to the q-exponential when [math]\displaystyle{ \kappa=1 }[/math]

The q-Weibull is a generalization of the Weibull, as it extends this distribution to the cases of finite support (q < 1) and to include heavy-tailed distributions [math]\displaystyle{ (q \ge 1+\frac{\kappa}{\kappa+1}) }[/math].

The q-Weibull is a generalization of the Lomax distribution (Pareto Type II), as it extends this distribution to the cases of finite support and adds the [math]\displaystyle{ \kappa }[/math] parameter. The Lomax parameters are:

[math]\displaystyle{ \alpha = { {2-q} \over {q-1}} ~,~ \lambda_\text{Lomax} = {1 \over {\lambda (q-1)}} }[/math]

As the Lomax distribution is a shifted version of the Pareto distribution, the q-Weibull for [math]\displaystyle{ \kappa=1 }[/math] is a shifted reparameterized generalization of the Pareto. When q > 1, the q-exponential is equivalent to the Pareto shifted to have support starting at zero. Specifically:

[math]\displaystyle{ \text{If } X \sim \operatorname{\mathit{q}-Weibull}(q,\lambda,\kappa = 1) \text{ and } Y \sim \left[\operatorname{Pareto} \left( x_m = {1 \over {\lambda (q-1)}}, \alpha = { {2-q} \over {q-1}} \right) -x_m \right], \text{ then } X \sim Y \, }[/math]

See also

• Constantino Tsallis
• Tsallis statistics
• Tsallis entropy
• Tsallis distribution
• q-Gaussian