Lomax distribution

Lomax

Probability density function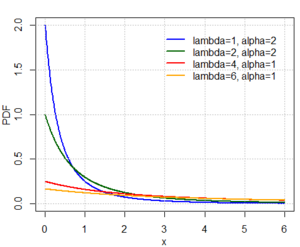
Cumulative distribution function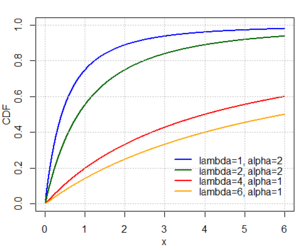
Parameters	[math]\displaystyle{ \alpha \gt 0 }[/math] shape (real) [math]\displaystyle{ \lambda \gt 0 }[/math] scale (real)
Support	[math]\displaystyle{ x \ge 0 }[/math]
PDF	[math]\displaystyle{ {\alpha \over \lambda} \left[{1 + {x \over \lambda}}\right]^{-(\alpha+1)} }[/math]
CDF	[math]\displaystyle{ 1 - \left[{1 + {x \over \lambda}}\right]^{-\alpha} }[/math]
Quantile	[math]\displaystyle{ \lambda \left[\left(1 - p\right)^{-\frac{1}{\alpha}} -1\right] }[/math]
Mean	[math]\displaystyle{ {\lambda \over {\alpha -1}} \text{ for } \alpha \gt 1 }[/math]; undefined otherwise
Median	[math]\displaystyle{ \lambda\left(\sqrt[\alpha]{2} - 1\right) }[/math]
Mode	0
Variance	[math]\displaystyle{ \begin{cases} {{\lambda^2 \alpha} \over {(\alpha-1)^2(\alpha-2)}} & \alpha \gt 2 \\ \infty & 1 \lt \alpha \le 2 \\ \text{Undefined} & \text{otherwise} \end{cases} }[/math]
Skewness	[math]\displaystyle{ \frac{2(1+\alpha)}{\alpha-3}\,\sqrt{\frac{\alpha-2}{\alpha}}\text{ for }\alpha\gt 3\, }[/math]
Kurtosis	[math]\displaystyle{ \frac{6(\alpha^3+\alpha^2-6\alpha-2)}{\alpha(\alpha-3)(\alpha-4)}\text{ for }\alpha\gt 4\, }[/math]

The Lomax distribution, conditionally also called the Pareto Type II distribution, is a heavy-tail probability distribution used in business, economics, actuarial science, queueing theory and Internet traffic modeling. It is named after K. S. Lomax. It is essentially a Pareto distribution that has been shifted so that its support begins at zero.

Characterization

Probability density function

The probability density function (pdf) for the Lomax distribution is given by

[math]\displaystyle{ p(x) = {\alpha \over \lambda} \left[{1 + {x \over \lambda}}\right]^{-(\alpha+1)}, \qquad x \geq 0, }[/math]

with shape parameter [math]\displaystyle{ \alpha \gt 0 }[/math] and scale parameter [math]\displaystyle{ \lambda \gt 0 }[/math]. The density can be rewritten in such a way that more clearly shows the relation to the Pareto Type I distribution. That is:

[math]\displaystyle{ p(x) = {{\alpha\lambda^\alpha} \over {(x + \lambda)^{\alpha+1}}} }[/math].

Non-central moments

The [math]\displaystyle{ \nu }[/math]th non-central moment [math]\displaystyle{ E\left[X^\nu\right] }[/math] exists only if the shape parameter [math]\displaystyle{ \alpha }[/math] strictly exceeds [math]\displaystyle{ \nu }[/math], when the moment has the value

[math]\displaystyle{ E\left(X^\nu\right) = \frac{\lambda^\nu \Gamma(\alpha - \nu)\Gamma(1 + \nu)}{\Gamma(\alpha)} }[/math]

Related distributions

Relation to the Pareto distribution

The Lomax distribution is a Pareto Type I distribution shifted so that its support begins at zero. Specifically:

[math]\displaystyle{ \text{If } Y \sim \mbox{Pareto}(x_m = \lambda, \alpha), \text{ then } Y - x_m \sim \mbox{Lomax}(\alpha,\lambda). }[/math]

The Lomax distribution is a Pareto Type II distribution with x_m=λ and μ=0:

[math]\displaystyle{ \text{If } X \sim \mbox{Lomax}(\alpha, \lambda) \text{ then } X \sim \text{P(II)}\left(x_m = \lambda, \alpha, \mu = 0\right). }[/math]

Relation to the generalized Pareto distribution

The Lomax distribution is a special case of the generalized Pareto distribution. Specifically:

[math]\displaystyle{ \mu = 0,~ \xi = {1 \over \alpha},~ \sigma = {\lambda \over \alpha} . }[/math]

Relation to the beta prime distribution

The Lomax distribution with scale parameter λ = 1 is a special case of the beta prime distribution. If X has a Lomax distribution, then [math]\displaystyle{ \frac{X}{\lambda} \sim \beta^\prime(1, \alpha) }[/math].

Relation to the F distribution

The Lomax distribution with shape parameter α = 1 and scale parameter λ = 1 has density [math]\displaystyle{ f(x) = \frac{1}{(1 + x)^2} }[/math], the same distribution as an F(2,2) distribution. This is the distribution of the ratio of two independent and identically distributed random variables with exponential distributions.

Relation to the q-exponential distribution

The Lomax distribution is a special case of the q-exponential distribution. The q-exponential extends this distribution to support on a bounded interval. The Lomax parameters are given by:

[math]\displaystyle{ \alpha = {{2 - q} \over {q - 1}}, ~ \lambda = {1 \over \lambda_q(q - 1)} . }[/math]

Relation to the (log-) logistic distribution

The logarithm of a Lomax(shape = 1.0, scale = λ)-distributed variable follows a logistic distribution with location log(λ) and scale 1.0. This implies that a Lomax(shape = 1.0, scale = λ)-distribution equals a log-logistic distribution with shape β = 1.0 and scale α = log(λ).

Gamma-exponential (scale-) mixture connection

The Lomax distribution arises as a mixture of exponential distributions where the mixing distribution of the rate is a gamma distribution. If λ|k,θ ~ Gamma(shape = k, scale = θ) and X|λ ~ Exponential(rate = λ) then the marginal distribution of X|k,θ is Lomax(shape = k, scale = 1/θ). Since the rate parameter may equivalently be reparameterized to a scale parameter, the Lomax distribution constitutes a scale mixture of exponentials (with the exponential scale parameter following an inverse-gamma distribution).

See also

• power law
• compound probability distribution
• hyperexponential distribution (finite mixture of exponentials)
• normal-exponential-gamma distribution (a normal scale mixture with Lomax mixing distribution)