q-exponential distribution
|
Probability density function  | |||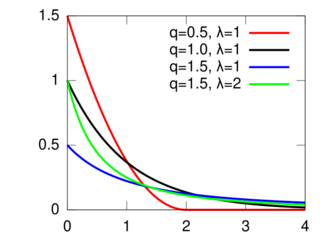
| Parameters |
[math]\displaystyle{ q \lt 2 }[/math] shape (real) [math]\displaystyle{ \lambda \gt 0 }[/math] rate (real) | ||
|---|---|---|---|
| Support |
[math]\displaystyle{ x \in [0, \infty) \text{ for } q \ge 1 }[/math] [math]\displaystyle{ x \in \left[0, \frac{1}{\lambda(1-q)}\right) \text{ for } q\lt 1 }[/math] | ||
| [math]\displaystyle{ (2-q) \lambda e_q^{-\lambda x} }[/math] | |||
| CDF | [math]\displaystyle{ 1-e_{q'}^{-\lambda x / q'} \text{ where } q' = \frac{1}{2-q} }[/math] | ||
| Mean |
[math]\displaystyle{ \frac{1}{\lambda (3-2q)} \text{ for } q \lt \frac{3}{2} }[/math] Otherwise undefined | ||
| Median | [math]\displaystyle{ \frac{-q' \ln_{q'}(1/2)}{\lambda} \text{ where } q' = \frac{1}{2-q} }[/math] | ||
| Mode | 0 | ||
| Variance | [math]\displaystyle{ \frac{q-2}{(2q-3)^2 (3q-4) \lambda^2} \text{ for } q \lt \frac{4}{3} }[/math] | ||
| Skewness | [math]\displaystyle{ \frac{2}{5-4q} \sqrt{\frac{3q-4}{q-2}} \text{ for } q \lt \frac{5}{4} }[/math] | ||
| Kurtosis | [math]\displaystyle{ 6\frac{-4q^3 + 17q^2 - 20q + 6} {(q-2)(4q-5)(5q-6)} \text{ for } q \lt \frac{6}{5} }[/math] | ||
The q-exponential distribution is a probability distribution arising from the maximization of the Tsallis entropy under appropriate constraints, including constraining the domain to be positive. It is one example of a Tsallis distribution. The q-exponential is a generalization of the exponential distribution in the same way that Tsallis entropy is a generalization of standard Boltzmann–Gibbs entropy or Shannon entropy.[1] The exponential distribution is recovered as [math]\displaystyle{ q \rightarrow 1. }[/math]
Originally proposed by the statisticians George Box and David Cox in 1964,[2] and known as the reverse Box–Cox transformation for [math]\displaystyle{ q=1-\lambda, }[/math] a particular case of power transform in statistics.
Characterization
Probability density function
The q-exponential distribution has the probability density function
- [math]\displaystyle{ (2-q) \lambda e_q(-\lambda x) }[/math]
where
- [math]\displaystyle{ e_q(x) = [1+(1-q)x]^{1/(1-q)} }[/math]
is the q-exponential if q ≠ 1. When q = 1, eq(x) is just exp(x).
Derivation
In a similar procedure to how the exponential distribution can be derived (using the standard Boltzmann–Gibbs entropy or Shannon entropy and constraining the domain of the variable to be positive), the q-exponential distribution can be derived from a maximization of the Tsallis Entropy subject to the appropriate constraints.
Relationship to other distributions
The q-exponential is a special case of the generalized Pareto distribution where
- [math]\displaystyle{ \mu = 0,\quad \xi = \frac{q-1}{2-q} ,\quad \sigma = \frac{1}{\lambda (2-q)}. }[/math]
The q-exponential is the generalization of the Lomax distribution (Pareto Type II), as it extends this distribution to the cases of finite support. The Lomax parameters are:
- [math]\displaystyle{ \alpha = \frac{2-q}{q-1} ,\quad \lambda_\mathrm{Lomax} = \frac{1}{\lambda (q-1)}. }[/math]
As the Lomax distribution is a shifted version of the Pareto distribution, the q-exponential is a shifted reparameterized generalization of the Pareto. When q > 1, the q-exponential is equivalent to the Pareto shifted to have support starting at zero. Specifically, if
- [math]\displaystyle{ X \sim \operatorname{\mathit{q}-Exp}(q,\lambda) \text{ and } Y \sim \left[\operatorname{Pareto}\left(x_m = \frac{1}{\lambda (q-1)}, \alpha = \frac{2-q}{q-1}\right) -x_m\right], }[/math]
then [math]\displaystyle{ X \sim Y. }[/math]
Generating random deviates
Random deviates can be drawn using inverse transform sampling. Given a variable U that is uniformly distributed on the interval (0,1), then
- [math]\displaystyle{ X = \frac{-q' \ln_{q'}(U)}{\lambda} \sim \operatorname{\mathit{q}-Exp}(q,\lambda) }[/math]
where [math]\displaystyle{ \ln_{q'} }[/math] is the q-logarithm and [math]\displaystyle{ q' = \frac{1}{2-q}. }[/math]
Applications
Being a power transform, it is a usual technique in statistics for stabilizing the variance, making the data more normal distribution-like and improving the validity of measures of association such as the Pearson correlation between variables. It has been found to be an accurate model for train delays.[3] It is also found in atomic physics and quantum optics, for example processes of molecular condensate creation via transition through the Feshbach resonance.[4]
See also
- Constantino Tsallis
- Tsallis statistics
- Tsallis entropy
- Tsallis distribution
- q-copula
- q-Gaussian
Notes
- ↑ Tsallis, C. Nonadditive entropy and nonextensive statistical mechanics-an overview after 20 years. Braz. J. Phys. 2009, 39, 337–356
- ↑ Box, George E. P.; Cox, D. R. (1964). "An analysis of transformations". Journal of the Royal Statistical Society, Series B 26 (2): 211–252.
- ↑ Keith Briggs and Christian Beck (2007). "Modelling train delays with q-exponential functions". Physica A 378 (2): 498–504. doi:10.1016/j.physa.2006.11.084. Bibcode: 2007PhyA..378..498B.
- ↑ C. Sun; N. A. Sinitsyn (2016). "Landau-Zener extension of the Tavis-Cummings model: Structure of the solution". Phys. Rev. A 94 (3): 033808. doi:10.1103/PhysRevA.94.033808. Bibcode: 2016PhRvA..94c3808S.
Further reading
- Juniper, J. (2007) "The Tsallis Distribution and Generalised Entropy: Prospects for Future Research into Decision-Making under Uncertainty", Centre of Full Employment and Equity, The University of Newcastle, Australia
External links
 |  |
