Quantities of information

A misleading information diagram showing additive and subtractive relationships among Shannon's basic quantities of information for correlated variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]. The area contained by both circles is the joint entropy [math]\displaystyle{ \Eta(X,Y) }[/math]. The circle on the left (red and violet) is the individual entropy [math]\displaystyle{ \Eta(X) }[/math], with the red being the conditional entropy [math]\displaystyle{ \Eta(X|Y) }[/math]. The circle on the right (blue and violet) is [math]\displaystyle{ \Eta(Y) }[/math], with the blue being [math]\displaystyle{ \Eta(Y|X) }[/math]. The violet is the mutual information [math]\displaystyle{ \operatorname{I}(X;Y) }[/math].

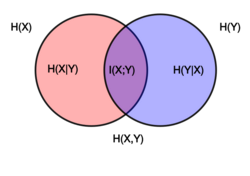
The mathematical theory of information is based on probability theory and statistics, and measures information with several quantities of information. The choice of logarithmic base in the following formulae determines the unit of information entropy that is used. The most common unit of information is the bit, or more correctly the shannon, based on the binary logarithm. Although "bit" is more frequently used in place of "shannon", its name is not distinguished from the bit as used in data-processing to refer to a binary value or stream regardless of its entropy (information content) Other units include the nat, based on the natural logarithm, and the hartley, based on the base 10 or common logarithm.

In what follows, an expression of the form [math]\displaystyle{ p \log p \, }[/math] is considered by convention to be equal to zero whenever [math]\displaystyle{ p }[/math] is zero. This is justified because [math]\displaystyle{ \lim_{p \rightarrow 0+} p \log p = 0 }[/math] for any logarithmic base.

Self-information

Shannon derived a measure of information content called the self-information or "surprisal" of a message [math]\displaystyle{ m }[/math]:

[math]\displaystyle{ \operatorname{I}(m) = \log \left( \frac{1}{p(m)} \right) = - \log( p(m) ) \, }[/math]

where [math]\displaystyle{ p(m) = \mathrm{Pr}(M=m) }[/math] is the probability that message [math]\displaystyle{ m }[/math] is chosen from all possible choices in the message space [math]\displaystyle{ M }[/math]. The base of the logarithm only affects a scaling factor and, consequently, the units in which the measured information content is expressed. If the logarithm is base 2, the measure of information is expressed in units of shannons or more often simply "bits" (a bit in other contexts is rather defined as a "binary digit", whose average information content is at most 1 shannon).

Information from a source is gained by a recipient only if the recipient did not already have that information to begin with. Messages that convey information over a certain (P=1) event (or one which is known with certainty, for instance, through a back-channel) provide no information, as the above equation indicates. Infrequently occurring messages contain more information than more frequently occurring messages.

It can also be shown that a compound message of two (or more) unrelated messages would have a quantity of information that is the sum of the measures of information of each message individually. That can be derived using this definition by considering a compound message [math]\displaystyle{ m\&n }[/math] providing information regarding the values of two random variables M and N using a message which is the concatenation of the elementary messages m and n, each of whose information content are given by [math]\displaystyle{ \operatorname{I}(m) }[/math] and [math]\displaystyle{ \operatorname{I}(n) }[/math] respectively. If the messages m and n each depend only on M and N, and the processes M and N are independent, then since [math]\displaystyle{ P(m\&n) = P(m) P(n) }[/math] (the definition of statistical independence) it is clear from the above definition that [math]\displaystyle{ \operatorname{I}(m\&n) = \operatorname{I}(m) + \operatorname{I}(n) }[/math].

An example: The weather forecast broadcast is: "Tonight's forecast: Dark. Continued darkness until widely scattered light in the morning." This message contains almost no information. However, a forecast of a snowstorm would certainly contain information since such does not happen every evening. There would be an even greater amount of information in an accurate forecast of snow for a warm location, such as Miami. The amount of information in a forecast of snow for a location where it never snows (impossible event) is the highest (infinity).

Entropy

The entropy of a discrete message space [math]\displaystyle{ M }[/math] is a measure of the amount of uncertainty one has about which message will be chosen. It is defined as the average self-information of a message [math]\displaystyle{ m }[/math] from that message space:

[math]\displaystyle{ \Eta(M) = \mathbb{E} \left[\operatorname{I}(M)\right] = \sum_{m \in M} p(m) \operatorname{I}(m) = -\sum_{m \in M} p(m) \log p(m). }[/math]

where

[math]\displaystyle{ \mathbb{E} [ - ] }[/math] denotes the expected value operation.

An important property of entropy is that it is maximized when all the messages in the message space are equiprobable (e.g. [math]\displaystyle{ p(m) = 1/|M| }[/math]). In this case [math]\displaystyle{ \Eta(M) = \log |M| }[/math].

Sometimes the function [math]\displaystyle{ \Eta }[/math] is expressed in terms of the probabilities of the distribution:

[math]\displaystyle{ \Eta(p_1, p_2, \ldots , p_k) = -\sum_{i=1}^k p_i \log p_i, }[/math] where each [math]\displaystyle{ p_i \geq 0 }[/math] and [math]\displaystyle{ \sum_{i=1}^k p_i = 1. }[/math]

An important special case of this is the binary entropy function:

[math]\displaystyle{ \Eta_\mbox{b}(p) = \Eta(p, 1-p) = - p \log p - (1-p)\log (1-p).\, }[/math]

Joint entropy

The joint entropy of two discrete random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] is defined as the entropy of the joint distribution of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math]:

[math]\displaystyle{ \Eta(X, Y) = \mathbb{E}_{X,Y} \left[-\log p(x,y)\right] = - \sum_{x, y} p(x, y) \log p(x, y) \, }[/math]

If [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are independent, then the joint entropy is simply the sum of their individual entropies.

(Note: The joint entropy should not be confused with the cross entropy, despite similar notations.)

Conditional entropy (equivocation)

Given a particular value of a random variable [math]\displaystyle{ Y }[/math], the conditional entropy of [math]\displaystyle{ X }[/math] given [math]\displaystyle{ Y=y }[/math] is defined as:

[math]\displaystyle{ \Eta(X|y) = \mathbb{E}_{\left[X|Y \right]} [-\log p(x|y)] = -\sum_{x \in X} p(x|y) \log p(x|y) }[/math]

where [math]\displaystyle{ p(x|y) = \frac{p(x,y)}{p(y)} }[/math] is the conditional probability of [math]\displaystyle{ x }[/math] given [math]\displaystyle{ y }[/math].

The conditional entropy of [math]\displaystyle{ X }[/math] given [math]\displaystyle{ Y }[/math], also called the equivocation of [math]\displaystyle{ X }[/math] about [math]\displaystyle{ Y }[/math] is then given by:

[math]\displaystyle{ \Eta(X|Y) = \mathbb{E}_Y \left[\Eta\left(X|y \right)\right] = -\sum_{y \in Y} p(y) \sum_{x \in X} p(x|y) \log p(x|y) = \sum_{x,y} p(x,y) \log \frac{p(y)}{p(x,y)}. }[/math]

This uses the conditional expectation from probability theory.

A basic property of the conditional entropy is that:

[math]\displaystyle{ \Eta(X|Y) = \Eta(X,Y) - \Eta(Y) .\, }[/math]

Kullback–Leibler divergence (information gain)

The Kullback–Leibler divergence (or information divergence, information gain, or relative entropy) is a way of comparing two distributions, a "true" probability distribution [math]\displaystyle{ p }[/math], and an arbitrary probability distribution [math]\displaystyle{ q }[/math]. If we compress data in a manner that assumes [math]\displaystyle{ q }[/math] is the distribution underlying some data, when, in reality, [math]\displaystyle{ p }[/math] is the correct distribution, Kullback–Leibler divergence is the number of average additional bits per datum necessary for compression, or, mathematically,

[math]\displaystyle{ D_{\mathrm{KL}}\bigl(p(X) \| q(X) \bigr) = \sum_{x \in X} p(x) \log \frac{p(x)}{q(x)}. }[/math]

It is in some sense the "distance" from [math]\displaystyle{ q }[/math] to [math]\displaystyle{ p }[/math], although it is not a true metric due to its not being symmetric.

Mutual information (transinformation)

It turns out that one of the most useful and important measures of information is the mutual information, or transinformation. This is a measure of how much information can be obtained about one random variable by observing another. The mutual information of [math]\displaystyle{ X }[/math] relative to [math]\displaystyle{ Y }[/math] (which represents conceptually the average amount of information about [math]\displaystyle{ X }[/math] that can be gained by observing [math]\displaystyle{ Y }[/math]) is given by:

[math]\displaystyle{ \operatorname{I}(X;Y) = \sum_{y\in Y} p(y)\sum_{x\in X} {p(x|y) \log \frac{p(x|y)}{p(x)}} = \sum_{x,y} p(x,y) \log \frac{p(x,y)}{p(x)\, p(y)}. }[/math]

A basic property of the mutual information is that:

[math]\displaystyle{ \operatorname{I}(X;Y) = \Eta(X) - \Eta(X|Y).\, }[/math]

That is, knowing [math]\displaystyle{ Y }[/math], we can save an average of [math]\displaystyle{ \operatorname{I}(X; Y) }[/math] bits in encoding [math]\displaystyle{ X }[/math] compared to not knowing [math]\displaystyle{ Y }[/math]. Mutual information is symmetric:

[math]\displaystyle{ \operatorname{I}(X;Y) = \operatorname{I}(Y;X) = \Eta(X) + \Eta(Y) - \Eta(X,Y).\, }[/math]

Mutual information can be expressed as the average Kullback–Leibler divergence (information gain) of the posterior probability distribution of [math]\displaystyle{ X }[/math] given the value of [math]\displaystyle{ Y }[/math] to the prior distribution on [math]\displaystyle{ X }[/math]:

[math]\displaystyle{ \operatorname{I}(X;Y) = \mathbb{E}_{p(y)} \left[D_{\mathrm{KL}}\bigl( p(X|Y=y) \| p(X) \bigr)\right]. }[/math]

In other words, this is a measure of how much, on the average, the probability distribution on [math]\displaystyle{ X }[/math] will change if we are given the value of [math]\displaystyle{ Y }[/math]. This is often recalculated as the divergence from the product of the marginal distributions to the actual joint distribution:

[math]\displaystyle{ \operatorname{I}(X; Y) = D_{\mathrm{KL}}\bigl(p(X,Y) \| p(X)p(Y) \bigr). }[/math]

Mutual information is closely related to the log-likelihood ratio test in the context of contingency tables and the multinomial distribution and to Pearson's χ² test: mutual information can be considered a statistic for assessing independence between a pair of variables, and has a well-specified asymptotic distribution.

Differential entropy

The basic measures of discrete entropy have been extended by analogy to continuous spaces by replacing sums with integrals and probability mass functions with probability density functions. Although, in both cases, mutual information expresses the number of bits of information common to the two sources in question, the analogy does not imply identical properties; for example, differential entropy may be negative.

The differential analogies of entropy, joint entropy, conditional entropy, and mutual information are defined as follows:

[math]\displaystyle{ h(X) = -\int_X f(x) \log f(x) \,dx }[/math]

[math]\displaystyle{ h(X,Y) = -\int_Y \int_X f(x,y) \log f(x,y) \,dx \,dy }[/math]

[math]\displaystyle{ h(X|y) = -\int_X f(x|y) \log f(x|y) \,dx }[/math]

[math]\displaystyle{ h(X|Y) = \int_Y \int_X f(x,y) \log \frac{f(y)}{f(x,y)} \,dx \,dy }[/math]

[math]\displaystyle{ \operatorname{I}(X;Y) = \int_Y \int_X f(x,y) \log \frac{f(x,y)}{f(x)f(y)} \,dx \,dy }[/math]

where [math]\displaystyle{ f(x,y) }[/math] is the joint density function, [math]\displaystyle{ f(x) }[/math] and [math]\displaystyle{ f(y) }[/math] are the marginal distributions, and [math]\displaystyle{ f(x|y) }[/math] is the conditional distribution.

See also

• Information theory