Rodrigues' rotation formula
In the theory of three-dimensional rotation, Rodrigues' rotation formula, named after Olinde Rodrigues, is an efficient algorithm for rotating a vector in space, given an axis and angle of rotation. By extension, this can be used to transform all three basis vectors to compute a rotation matrix in SO(3), the group of all rotation matrices, from an axis–angle representation. In terms of Lie theory, the Rodrigues' formula provides an algorithm to compute the exponential map from the Lie algebra so(3) to its Lie group SO(3).
This formula is variously credited to Leonhard Euler, Olinde Rodrigues, or a combination of the two. A detailed historical analysis in 1989 concluded that the formula should be attributed to Euler, and recommended calling it "Euler's finite rotation formula."[1] This proposal has received notable support,[2] but some others have viewed the formula as just one of many variations of the Euler–Rodrigues formula, thereby crediting both.[3]
Statement
If v is a vector in ℝ3 and k is a unit vector describing an axis of rotation about which v rotates by an angle θ according to the right hand rule, the Rodrigues formula for the rotated vector vrot is
[math]\displaystyle{ \mathbf{v}_\mathrm{rot} = \mathbf{v} \cos\theta + (\mathbf{k} \times \mathbf{v})\sin\theta + \mathbf{k} ~(\mathbf{k} \cdot \mathbf{v}) (1 - \cos\theta)\,. }[/math]
The intuition of the above formula is that the first term scales the vector down, while the second skews it (via vector addition) toward the new rotational position. The third term re-adds the height (relative to [math]\displaystyle{ \textbf{k} }[/math]) that was lost by the first term.
An alternative statement is to write the axis vector as a cross product a × b of any two nonzero vectors a and b which define the plane of rotation, and the sense of the angle θ is measured away from a and towards b. Letting α denote the angle between these vectors, the two angles θ and α are not necessarily equal, but they are measured in the same sense. Then the unit axis vector can be written
- [math]\displaystyle{ \mathbf{k} = \frac{\mathbf{a}\times\mathbf{b}}{|\mathbf{a}\times\mathbf{b}|} = \frac{\mathbf{a}\times\mathbf{b}}{|\mathbf{a}||\mathbf{b}|\sin\alpha}\,. }[/math]
This form may be more useful when two vectors defining a plane are involved. An example in physics is the Thomas precession which includes the rotation given by Rodrigues' formula, in terms of two non-collinear boost velocities, and the axis of rotation is perpendicular to their plane.
Derivation
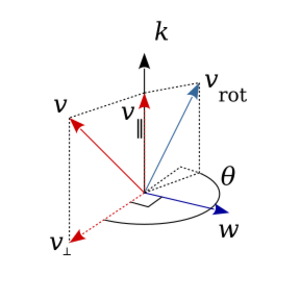
Let k be a unit vector defining a rotation axis, and let v be any vector to rotate about k by angle θ (right hand rule, anticlockwise in the figure), producing the rotated vector [math]\displaystyle{ \mathbb{v}_{\text{rot}} }[/math].
Using the dot and cross products, the vector v can be decomposed into components parallel and perpendicular to the axis k,
- [math]\displaystyle{ \mathbf{v} = \mathbf{v}_\parallel + \mathbf{v}_\perp \,, }[/math]
where the component parallel to k is called the vector projection of v on k,
- [math]\displaystyle{ \mathbf{v}_\parallel = (\mathbf{v} \cdot \mathbf{k}) \mathbf{k} }[/math],
and the component perpendicular to k is called the vector rejection of v from k:
- [math]\displaystyle{ \mathbf{v}_{\perp} = \mathbf{v} - \mathbf{v}_{\parallel} = \mathbf{v} - (\mathbf{k} \cdot \mathbf{v}) \mathbf{k} = - \mathbf{k}\times(\mathbf{k}\times\mathbf{v}) }[/math],
where the last equality follows from the vector triple product formula: [math]\displaystyle{ \mathbf{a}\times (\mathbf{b} \times \mathbf{c}) = (\mathbf{a} \cdot \mathbf{c})\mathbf{b} - (\mathbf{a} \cdot \mathbf{b})\mathbf{c} }[/math]. Finally, the vector [math]\displaystyle{ \mathbf{k} \times \mathbf{v}_{\perp} = \mathbf{k} \times \mathbf{v} }[/math] is a copy of [math]\displaystyle{ \mathbf{v}_{\perp} }[/math] rotated 90° around [math]\displaystyle{ \mathbf{k} }[/math]. Thus the three vectors [math]\displaystyle{ \mathbf{k}\,,\ \mathbf{v}_{\perp}\,,\, \mathbf{k} \times \mathbf{v} }[/math] form a right-handed orthogonal basis of [math]\displaystyle{ \mathbb{R}^3 }[/math], with the last two vectors of equal length.
Under the rotation, the component [math]\displaystyle{ \mathbf{v}_{\parallel} }[/math] parallel to the axis will not change magnitude nor direction:
- [math]\displaystyle{ \mathbf{v}_{\parallel\mathrm{rot}} = \mathbf{v}_\parallel \,; }[/math]
while the perpendicular component will retain its magnitude but rotate its direction in the perpendicular plane spanned by [math]\displaystyle{ \mathbf{v}_{\perp} }[/math] and [math]\displaystyle{ \mathbf{k} \times \mathbf{v} }[/math], according to
- [math]\displaystyle{ \mathbf{v}_{\perp\mathrm{rot}} = \cos(\theta) \mathbf{v}_\perp + \sin(\theta) \mathbf{k}\times\mathbf{v}_\perp = \cos(\theta) \mathbf{v}_\perp + \sin(\theta) \mathbf{k}\times\mathbf{v} \,, }[/math]
in analogy with the planar polar coordinates (r, θ) in the Cartesian basis ex, ey:
- [math]\displaystyle{ \mathbf{r} = r\cos(\theta) \mathbf{e}_x + r\sin(\theta) \mathbf{e}_y \,. }[/math]
Now the full rotated vector is:
- [math]\displaystyle{ \mathbf{v}_{\mathrm{rot}} = \mathbf{v}_{\parallel\mathrm{rot}} + \mathbf{v}_{\perp\mathrm{rot}} = \mathbf{v}_\parallel + \cos(\theta) \, \mathbf{v}_\perp + \sin(\theta) \mathbf{k}\times\mathbf{v} . }[/math]
Substituting [math]\displaystyle{ \mathbf{v}_{\perp } = \mathbf{v} - \mathbf{v}_{\|} }[/math] or [math]\displaystyle{ \mathbf{v}_{\| } = \mathbf{v} - \mathbf{v}_{\perp} }[/math] in the last expression gives respectively:[math]\displaystyle{ \mathbf{v}_{\text{rot}} = \cos(\theta) \, \mathbf{v} + (1 - \cos\theta)(\mathbf{k} \cdot \mathbf{v})\mathbf{k} + \sin(\theta) \mathbf{k}\times\mathbf{v}, }[/math][math]\displaystyle{ \mathbf{v}_{\text{rot}} = \mathbf{v} + (1-\cos\theta)\mathbf{k}\times(\mathbf{k}\times\mathbf{v}) + \sin(\theta) \mathbf{k}\times\mathbf{v}. }[/math]
Matrix notation
The linear transformation on [math]\displaystyle{ \mathbf{v}\isin\mathbb{R}^3 }[/math] defined by the cross product [math]\displaystyle{ \mathbf{v} \mapsto \mathbf{k} \times \mathbf{v} }[/math] is given in coordinates by representing v and k × v as column matrices:
- [math]\displaystyle{ \begin{bmatrix} (\mathbf{k}\times\mathbf{v})_x \\ (\mathbf{k}\times\mathbf{v})_y \\ (\mathbf{k}\times\mathbf{v})_z \end{bmatrix} = \begin{bmatrix} k_y v_z - k_z v_y \\ k_z v_x - k_x v_z \\ k_x v_y - k_y v_x \end{bmatrix} = \left[\begin{array}{rrr} 0\ \, & -k_z & k_y \\ k_z & 0\ \, & -k_x \\ -k_y & k_x & 0\ \, \end{array}\right] \begin{bmatrix} v_x \\ v_y \\ v_z \end{bmatrix} \,. }[/math]
That is, the matrix of this linear transformation (with respect to standard coordinates) is the cross-product matrix:
- [math]\displaystyle{ \mathbf{K}= \left[\begin{array}{rrr} 0\ \, & -k_z & k_y \\ k_z & 0\ \, & -k_x \\ -k_y & k_x & 0\ \, \end{array}\right]\,. }[/math]
That is to say,
- [math]\displaystyle{ \mathbf{k}\times\mathbf{v}=\mathbf{K}\mathbf{v}, \qquad\qquad \mathbf{k}\times(\mathbf{k}\times\mathbf{v})=\mathbf{K}(\mathbf{K}\mathbf{v}) = \mathbf{K}^2\mathbf{v} \,. }[/math]
The last formula in the previous section can therefore be written as:
- [math]\displaystyle{ \mathbf{v}_{\mathrm{rot}} = \mathbf{v} + (\sin\theta) \mathbf{K}\mathbf{v} + (1 - \cos\theta)\mathbf{K}^2\mathbf{v}\,. }[/math]
Collecting terms allows the compact expression
- [math]\displaystyle{ \mathbf{v}_\mathrm{rot} = \mathbf{R}\mathbf{v} }[/math]
where
[math]\displaystyle{ \mathbf{R} = \mathbf{I} + (\sin\theta) \mathbf{K} + (1-\cos\theta)\mathbf{K}^2 }[/math]
is the rotation matrix through an angle θ counterclockwise about the axis k, and I the 3 × 3 identity matrix.[4] This matrix R is an element of the rotation group SO(3) of ℝ3, and K is an element of the Lie algebra [math]\displaystyle{ \mathfrak{so}(3) }[/math] generating that Lie group (note that K is skew-symmetric, which characterizes [math]\displaystyle{ \mathfrak{so}(3) }[/math]).
In terms of the matrix exponential,
- [math]\displaystyle{ \mathbf{R} = \exp (\theta\mathbf{K})\,. }[/math]
To see that the last identity holds, one notes that
- [math]\displaystyle{ \mathbf{R}(\theta) \mathbf{R}(\phi) = \mathbf{R} (\theta+\phi), \quad \mathbf{R}(0) = \mathbf{I}\,, }[/math]
characteristic of a one-parameter subgroup, i.e. exponential, and that the formulas match for infinitesimal θ.
For an alternative derivation based on this exponential relationship, see exponential map from [math]\displaystyle{ \mathfrak{so}(3) }[/math] to SO(3). For the inverse mapping, see log map from SO(3) to [math]\displaystyle{ \mathfrak{so}(3) }[/math].
The Hodge dual of the rotation [math]\displaystyle{ \mathbf{R} }[/math] is just [math]\displaystyle{ \mathbf{R}^* = -\sin(\theta)\mathbf{k} }[/math] which enables the extraction of both the axis of rotation and the sine of the angle of the rotation from the rotation matrix itself, with the usual ambiguity,
- [math]\displaystyle{ \begin{align} \sin(\theta) &= \sigma \left|\mathbf{R}^*\right| \\[3pt] \mathbf{k} &= -\frac{\sigma\mathbf{R}^*}{\left|\mathbf{R}^*\right|} \end{align} }[/math]
where [math]\displaystyle{ \sigma = \pm 1 }[/math]. The above simple expression results from the fact that the Hodge duals of [math]\displaystyle{ \mathbf{I} }[/math] and [math]\displaystyle{ \mathbf{K}^2 }[/math] are zero, and [math]\displaystyle{ \mathbf{K}^* = -\mathbf{k} }[/math].
When applying the Rodrigues' formula, however, the usual ambiguity could be removed with an extended form of the formula.a
See also
- Axis angle
- Rotation (mathematics)
- SO(3) and SO(4)
- Euler–Rodrigues formula
References
- ↑ Cheng, Hui; Gupta, K. C. (March 1989). "An Historical Note on Finite Rotations". Journal of Applied Mechanics (American Society of Mechanical Engineers) 56 (1): 139–145. https://doi.org/10.1115/1.3176034. Retrieved 2022-04-11.
- ↑ Fraiture, Luc (2009). "A History of the Description of the Three-Dimensional Finite Rotation". The Journal of the Astronautical Sciences (Springer) 57: 207–232. https://doi.org/10.1007/BF03321502. Retrieved 2022-04-15.
- ↑ Dai, Jian S. (October 2015). "Euler–Rodrigues formula variations, quaternion conjugation and intrinsic connections". Mechanism and Machine Theory (Elsevier) 92: 144–152. https://doi.org/10.1016/j.mechmachtheory.2015.03.004. Retrieved 2022-04-14.
- ↑ Belongie, Serge. "Rodrigues' Rotation Formula" (in en). https://mathworld.wolfram.com/RodriguesRotationFormula.html.
- Leonhard Euler, "Problema algebraicum ob affectiones prorsus singulares memorabile", Commentatio 407 Indicis Enestoemiani, Novi Comm. Acad. Sci. Petropolitanae 15 (1770), 75–106.
- Olinde Rodrigues, "Des lois géométriques qui régissent les déplacements d'un système solide dans l'espace, et de la variation des coordonnées provenant de ces déplacements considérés indépendants des causes qui peuvent les produire", Journal de Mathématiques Pures et Appliquées 5 (1840), 380–440. online.
- Friedberg, Richard (2022). "Rodrigues, Olinde: "Des lois géométriques qui régissent les déplacements d'un systéme solide...", translation and commentary". arXiv:2211.07787.
- Don Koks, (2006) Explorations in Mathematical Physics, Springer Science+Business Media, LLC. ISBN 0-387-30943-8. Ch.4, pps 147 et seq. A Roundabout Route to Geometric Algebra
- ^a Liang, Kuo Kan (2018). "Efficient conversion from rotating matrix to rotation axis and angle by extending Rodrigues' formula". arXiv:1810.02999 [cs].
External links
- Johan E. Mebius, Derivation of the Euler-Rodrigues formula for three-dimensional rotations from the general formula for four-dimensional rotations., arXiv General Mathematics 2007.
- For another descriptive example see: http://chrishecker.com/Rigid_Body_Dynamics#Physics_Articles, Chris Hecker, physics section, part 4. "The Third Dimension" – on page 3, section ``Axis and Angle, http://chrishecker.com/images/b/bb/Gdmphys4.pdf
fr:Rotation vectorielle#Cas général
 |  |
