Physics:Thomas precession
| Part of a series on |
| Spacetime |
|---|
 |
|
Special relativity General relativity |

In physics, the Thomas precession, named after Llewellyn Thomas, is a relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope and relates the angular velocity of the spin of a particle following a curvilinear orbit to the angular velocity of the orbital motion.
For a given inertial frame, if a second frame is Lorentz-boosted relative to it, and a third boosted relative to the second, but non-collinear with the first boost, then the Lorentz transformation between the first and third frames involves a combined boost and rotation, known as the "Wigner rotation" or "Thomas rotation". For accelerated motion, the accelerated frame has an inertial frame at every instant. Two boosts a small time interval (as measured in the lab frame) apart leads to a Wigner rotation after the second boost. In the limit the time interval tends to zero, the accelerated frame will rotate at every instant, so the accelerated frame rotates with an angular velocity.
The precession can be understood geometrically as a consequence of the fact that the space of velocities in relativity is hyperbolic, and so parallel transport of a vector (the gyroscope's angular velocity) around a circle (its linear velocity) leaves it pointing in a different direction, or understood algebraically as being a result of the non-commutativity of Lorentz transformations. Thomas precession gives a correction to the spin–orbit interaction in quantum mechanics, which takes into account the relativistic time dilation between the electron and the nucleus of an atom.
Thomas precession is a kinematic effect in the flat spacetime of special relativity. In the curved spacetime of general relativity, Thomas precession combines with a geometric effect to produce de Sitter precession. Although Thomas precession (net rotation after a trajectory that returns to its initial velocity) is a purely kinematic effect, it only occurs in curvilinear motion and therefore cannot be observed independently of some external force causing the curvilinear motion such as that caused by an electromagnetic field, a gravitational field or a mechanical force, so Thomas precession is usually accompanied by dynamical effects.[1]
If the system experiences no external torque, e.g., in external scalar fields, its spin dynamics are determined only by the Thomas precession. A single discrete Thomas rotation (as opposed to the series of infinitesimal rotations that add up to the Thomas precession) is present in situations anytime there are three or more inertial frames in non-collinear motion, as can be seen using Lorentz transformations.
History
Thomas precession in relativity was already known to Ludwik Silberstein,[2] in 1914. But the only knowledge Thomas had of relativistic precession came from de Sitter's paper on the relativistic precession of the moon, first published in a book by Eddington.[3]
In 1925 Thomas relativistically recomputed the precessional frequency of the doublet separation in the fine structure of the atom. He thus found the missing factor 1/2, which came to be known as the Thomas half.
This discovery of the relativistic precession of the electron spin led to the understanding of the significance of the relativistic effect. The effect was consequently named "Thomas precession".
Introduction
Definition
Consider a physical system moving through Minkowski spacetime. Assume that there is at any moment an inertial system such that in it, the system is at rest. This assumption is sometimes called the third postulate of relativity.[4] This means that at any instant, the coordinates and state of the system can be Lorentz transformed to the lab system through some Lorentz transformation.
Let the system be subject to external forces that produce no torque with respect to its center of mass in its (instantaneous) rest frame. The condition of "no torque" is necessary to isolate the phenomenon of Thomas precession. As a simplifying assumption one assumes that the external forces bring the system back to its initial velocity after some finite time. Fix a Lorentz frame O such that the initial and final velocities are zero.
The Pauli–Lubanski spin vector Sμ is defined to be (0, Si) in the system's rest frame, with Si the angular-momentum three-vector about the center of mass. In the motion from initial to final position, Sμ undergoes a rotation, as recorded in O, from its initial to its final value. This continuous change is the Thomas precession.[5]
Statement
Consider the motion of a particle. Introduce a lab frame Σ in which an observer can measure the relative motion of the particle. At each instant of time the particle has an inertial frame in which it is at rest. Relative to this lab frame, the instantaneous velocity of the particle is v(t) with magnitude |v| = v bounded by the speed of light c, so that 0 ≤ v < c. Here the time t is the coordinate time as measured in the lab frame, not the proper time of the particle.
Apart from the upper limit on magnitude, the velocity of the particle is arbitrary and not necessarily constant, its corresponding vector of acceleration is a = dv(t)/dt. As a result of the Wigner rotation at every instant, the particle's frame precesses with an angular velocity given by the equation[6][7][8][9]
where × is the cross product and
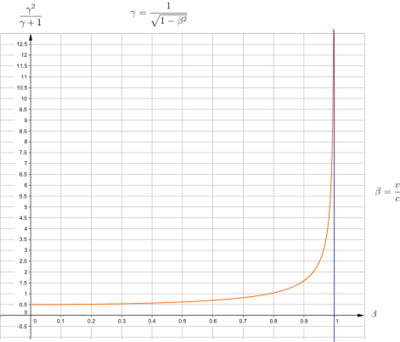
is the instantaneous Lorentz factor, a function of the particle's instantaneous velocity. Like any angular velocity, ωT is a pseudovector; its magnitude is the angular speed the particle's frame precesses (in radians per second), and the direction points along the rotation axis. As is usual, the right-hand convention of the cross product is used (see right-hand rule).
The precession depends on accelerated motion, and the non-collinearity of the particle's instantaneous velocity and acceleration. No precession occurs if the particle moves with uniform velocity (constant v so a = 0), or accelerates in a straight line (in which case v and a are parallel or antiparallel so their cross product is zero). The particle has to move in a curve, say an arc, spiral, helix, or a circular orbit or elliptical orbit, for its frame to precess. The angular velocity of the precession is a maximum if the velocity and acceleration vectors are perpendicular throughout the motion (a circular orbit), and is large if their magnitudes are large (the magnitude of v is almost c).
In the non-relativistic limit, v → 0 so γ → 1, and the angular velocity is approximately
The factor of 1/2 turns out to be the critical factor to agree with experimental results. It is informally known as the "Thomas half".
Mathematical explanation
Lorentz transformations
The description of relative motion involves Lorentz transformations, and it is convenient to use them in matrix form; symbolic matrix expressions summarize the transformations and are easy to manipulate, and when required the full matrices can be written explicitly. Also, to prevent extra factors of c cluttering the equations, it is convenient to use the definition β(t) = v(t)/c with magnitude |β| = β such that 0 ≤ β < 1.
The spacetime coordinates of the lab frame are collected into a 4×1 column vector, and the boost is represented as a 4×4 symmetric matrix, respectively
and turn
is the Lorentz factor of β. In other frames, the corresponding coordinates are also arranged into column vectors. The inverse matrix of the boost corresponds to a boost in the opposite direction, and is given by B(β)−1 = B(−β).
At an instant of lab-recorded time t measured in the lab frame, the transformation of spacetime coordinates from the lab frame Σ to the particle's frame Σ′ is
-
()
and at later lab-recorded time t + Δt we can define a new frame Σ′′ for the particle, which moves with velocity β + Δβ relative to Σ, and the corresponding boost is
-
()
The vectors β and Δβ are two separate vectors. The latter is a small increment, and can be conveniently split into components parallel (‖) and perpendicular (⊥) to β[nb 1]
Combining (1) and (2) obtains the Lorentz transformation between Σ′ and Σ′′,
-
()
and this composition contains all the required information about the motion between these two lab times. Notice B(β + Δβ)B(−β) and B(β + Δβ) are infinitesimal transformations because they involve a small increment in the relative velocity, while B(−β) is not.
The composition of two boosts equates to a single boost combined with a Wigner rotation about an axis perpendicular to the relative velocities;
-
()
The rotation is given by is a 4×4 rotation matrix R in the axis–angle representation, and coordinate systems are taken to be right-handed. This matrix rotates 3d vectors anticlockwise about an axis (active transformation), or equivalently rotates coordinate frames clockwise about the same axis (passive transformation). The axis-angle vector Δθ parametrizes the rotation, its magnitude Δθ is the angle Σ′′ has rotated, and direction is parallel to the rotation axis, in this case the axis is parallel to the cross product (−β)×(β + Δβ) = −β×Δβ. If the angles are negative, then the sense of rotation is reversed. The inverse matrix is given by R(Δθ)−1 = R(−Δθ).
Corresponding to the boost is the (small change in the) boost vector Δb, with magnitude and direction of the relative velocity of the boost (divided by c). The boost B(Δb) and rotation R(Δθ) here are infinitesimal transformations because Δb and rotation Δθ are small.
The rotation gives rise to the Thomas precession, but there is a subtlety. To interpret the particle's frame as a co-moving inertial frame relative to the lab frame, and agree with the non-relativistic limit, we expect the transformation between the particle's instantaneous frames at times t and t + Δt to be related by a boost without rotation. Combining (3) and (4) and rearranging gives
-
()
where another instantaneous frame Σ′′′ is introduced with coordinates X′′′, to prevent conflation with Σ′′. To summarize the frames of reference: in the lab frame Σ an observer measures the motion of the particle, and three instantaneous inertial frames in which the particle is at rest are Σ′ (at time t), Σ′′ (at time t + Δt), and Σ′′′ (at time t + Δt). The frames Σ′′ and Σ′′′ are at the same location and time, they differ only by a rotation. By contrast Σ′ and Σ′′′ differ by a boost and lab time interval Δt.
Relating the coordinates X′′′ to the lab coordinates X via (5) and (2);
-
()
the frame Σ′′′ is rotated in the negative sense.
The rotation is between two instants of lab time. As Δt → 0, the particle's frame rotates at every instant, and the continuous motion of the particle amounts to a continuous rotation with an angular velocity at every instant. Dividing −Δθ by Δt, and taking the limit Δt → 0, the angular velocity is by definition
-
()
It remains to find what Δθ precisely is.
Extracting the formula
The composition can be obtained by explicitly calculating the matrix product. The boost matrix of β + Δβ will require the magnitude and Lorentz factor of this vector. Since Δβ is small, terms of "second order" |Δβ|2, (Δβx)2, (Δβy)2, ΔβxΔβy and higher are negligible. Taking advantage of this fact, the magnitude squared of the vector is
and expanding the Lorentz factor of β + Δβ as a power series gives to first order in Δβ,
using the Lorentz factor γ of β as above.
To simplify the calculation without loss of generality, take the direction of β to be entirely in the x direction, and Δβ in the xy plane, so the parallel component is along the x direction while the perpendicular component is along the y direction. The axis of the Wigner rotation is along the z direction. In the Cartesian basis ex, ey, ez, a set of mutually perpendicular unit vectors in their indicated directions, we have
This simplified setup allows the boost matrices to be given explicitly with the minimum number of matrix entries. In general, of course, β and Δβ can be in any plane, the final result given later will not be different.
Explicitly, at time t the boost is in the negative x direction
and the boost at the time t + Δt is
where γ is the Lorentz factor of β, not β + Δβ. The composite transformation is then the matrix product
Introducing the boost generators
and rotation generators
along with the dot product · facilitates the coordinate independent expression
which holds if β and Δβ lie in any plane. This is an infinitesimal Lorentz transformation in the form of a combined boost and rotation[nb 2]
where
After dividing Δθ by Δt and taking the limit as in (7), one obtains the instantaneous angular velocity
where a is the acceleration of the particle as observed in the lab frame. No forces were specified or used in the derivation so the precession is a kinematical effect - it arises from the geometric aspects of motion. However, forces cause accelerations, so the Thomas precession is observed if the particle is subject to forces.
Thomas precession can also be derived using the Fermi-Walker transport equation.[10] One assumes uniform circular motion in flat Minkowski spacetime. The spin 4-vector is orthogonal to the velocity 4-vector. Fermi-Walker transport preserves this relation. One finds that the dot product of the acceleration 4-vector with the spin 4-vector varies sinusoidally with time with an angular frequency γω, where ω is the angular frequency of the circular motion and γ=1/√(1-v^2/c^2), the Lorentz factor. This is easily shown by taking the second time derivative of that dot product. Because this angular frequency exceeds ω, the spin precesses in the retrograde direction. The difference (γ-1)ω is the Thomas precession angular frequency already given, as is simply shown by realizing that the magnitude of the 3-acceleration is ω v.
Applications
In electron orbitals
In quantum mechanics Thomas precession is a correction to the spin-orbit interaction, which takes into account the relativistic time dilation between the electron and the nucleus in hydrogenic atoms.
Basically, it states that spinning objects precess when they accelerate in special relativity because Lorentz boosts do not commute with each other.
To calculate the spin of a particle in a magnetic field, one must also take into account Larmor precession.
In a Foucault pendulum
The rotation of the swing plane of Foucault pendulum can be treated as a result of parallel transport of the pendulum in a 2-dimensional sphere of Euclidean space. The hyperbolic space of velocities in Minkowski spacetime represents a 3-dimensional (pseudo-) sphere with imaginary radius and imaginary timelike coordinate. Parallel transport of a spinning particle in relativistic velocity space leads to Thomas precession, which is similar to the rotation of the swing plane of a Foucault pendulum.[11] The angle of rotation in both cases is determined by the area integral of curvature in agreement with the Gauss–Bonnet theorem.
Thomas precession gives a correction to the precession of a Foucault pendulum. For a Foucault pendulum located in the city of Nijmegen in the Netherlands the correction is:
Note that it is more than two orders of magnitude smaller than the precession due to the general-relativistic correction arising from frame-dragging, the Lense–Thirring precession.
See also
Remarks
- ↑ Explicitly, using vector projection and rejection relative to the direction of β gives
- ↑ The rotation and boost matrices (each infinitesimal) are given by
Notes
- ↑ Malykin 2006
- ↑ Silberstein 1914, p. 169
- ↑ Eddington 1924
- ↑ Goldstein 1980
- ↑ Ben-Menahem 1986
- ↑ Jackson 1975, p. 543–546
- ↑ Goldstein 1980, p. 288
- ↑ Sard 1970, p. 280
- ↑ Sexl & Urbantke 2001, p. 42
- ↑ Misner, Thorne, and Wheeler, Gravitation, p 165, pp 175-176
- ↑ Krivoruchenko 2009
References
- Thomas L H The kinematics of an electron with an axis, Phil. Mag. 7 1927 1-23
- Ben-Menahem, A. (1985). "Wigner's rotation revisited". Am. J. Phys. 53 (1): 62–66. doi:10.1119/1.13953. Bibcode: 1985AmJPh..53...62B.
- Ben-Menahem, S. (1986). "The Thomas precession and velocityspace curvature". J. Math. Phys. 27 (5): 1284–1286. doi:10.1063/1.527132. Bibcode: 1986JMP....27.1284B.
- Cushing, J. T. (1967). "Vector Lorentz Transformations". Am. J. Phys. 35 (9): 858–862. doi:10.1119/1.1974267. Bibcode: 1967AmJPh..35..858C.
- Einstein, A. (1922), "Sidelights on relativity", Nature (London: Methuen) 112 (2809): 319, doi:10.1038/112319a0, Bibcode: 1923Natur.112..319., http://www.gutenberg.org/ebooks/7333; (Project Gutenberg Ebook)
- Eddington, A.S. (1924). The Mathematical Theory of Relativity. Cambridge University Press. http://www-history.mcs.st-and.ac.uk/Extras/Eddington_relativity.html; (Introduction)
- Kroemer, H. (January 2004). "The Thomas precession factor in spin-orbit interaction". Am. J. Phys. 72 (1): 51–52. doi:10.1119/1.1615526. Bibcode: 2004AmJPh..72...51K. http://www.ece.ucsb.edu/Faculty/Kroemer/pubs/13_04Thomas.pdf.
- Krivoruchenko, M. I. (2009). "Rotation of the swing plane of Foucault's pendulum and Thomas spin precession: Two faces of one coin". Phys. Usp. 52 (8): 821–829. doi:10.3367/UFNe.0179.200908e.0873. Bibcode: 2009PhyU...52..821K.
- Malykin, G. B. (2006). "Thomas precession: correct and incorrect solutions". Phys. Usp. 49 (8): 83 pp. doi:10.1070/PU2006v049n08ABEH005870. Bibcode: 2006PhyU...49..837M.
- Mocanu, C.I. (1992). "On the relativistic velocity composition paradox and the Thomas rotation". Found. Phys. Lett. 5 (5): 443–456. doi:10.1007/BF00690425. ISSN 0894-9875. Bibcode: 1992FoPhL...5..443M.
- Rebilas, K. (2013). "Comment on Elementary analysis of the special relativistic combination of velocities, Wigner rotation and Thomas precession". Eur. J. Phys. 34 (3): L55–L61. doi:10.1088/0143-0807/34/3/L55. Bibcode: 2013EJPh...34L..55R. (free access)
- Rhodes, J. A.; Semon, M. D. (2005). "Relativistic velocity space, Wigner rotation and Thomas precession". Am. J. Phys. 72 (7): 943–960. doi:10.1119/1.1652040. Bibcode: 2005APS..NES..R001S.
- Silberstein, L. (1914). The Theory of Relativity. London: Macmillan Publishers. https://archive.org/details/theoryofrelativi00silbrich.
- Thomas, L. H. (1926). "Motion of the spinning electron". Nature 117 (2945): 514. doi:10.1038/117514a0. Bibcode: 1926Natur.117..514T.
- Ungar, A. A. (1988). "Thomas rotation and parameterization of the Lorentz group". Foundations of Physics Letters 1 (1): 57–81. doi:10.1007/BF00661317. ISSN 0894-9875. Bibcode: 1988FoPhL...1...57U.
- Weinberg, S. (2002), The Quantum Theory of Fields, 1, Cambridge University Press, ISBN 978-0-521-55001-7, https://archive.org/details/quantumtheoryoff00stev
- Wigner, E. P. (1939), "On unitary representations of the inhomogeneous Lorentz group", Annals of Mathematics 40 (1): 149–204, doi:10.2307/1968551, Bibcode: 1939AnMat..40..149W.
Textbooks
- Goldstein, H. (1980). "Chapter 7". Classical Mechanics (2nd ed.). Reading MA: Addison-Wesley. ISBN 978-0-201-02918-5.
- Jackson, J. D. (1999). "Chapter 11". Classical Electrodynamics (3d ed.). John Wiley & Sons. ISBN 978-0-471-30932-1. https://archive.org/details/classicalelectro0000jack_e8g9.
- Jackson, J. D. (1975). "Chapter 11". Classical Electrodynamics (2nd ed.). John Wiley & Sons. pp. 542–545. ISBN 978-0-471-43132-9. https://archive.org/details/classicalelectro00jack_0.
- Landau, L.D.; Lifshitz, E.M. (2002). The Classical Theory of Fields. Course of Theoretical Physics. 2 (4th ed.). Butterworth–Heinemann. p. 38. ISBN 0-7506-2768-9.
- Rindler, W. (2006). "Chapter 9". Relativity Special, General and Cosmological (2nd ed.). Dallas: Oxford University Press. ISBN 978-0-19-856732-5.
- Ryder, L. H. (1996). Quantum Field Theory (2nd ed.). Cambridge: Cambridge University Press. ISBN 978-0521478144.
- Sard, R. D. (1970). Relativistic Mechanics - Special Relativity and Classical Particle Dynamics. New York: W. A. Benjamin. ISBN 978-0805384918. https://archive.org/details/relativisticmech0000sard.
- Sexl, R. U.; Urbantke, H. K. (2001). Relativity, Groups Particles. Special Relativity and Relativistic Symmetry in Field and Particle Physics. Springer. pp. 38–43. ISBN 978-3211834435. https://books.google.com/books?id=iyj0CAAAQBAJ&q=sexl+relativity.
External links
- Mathpages article on Thomas Precession
- Alternate, detailed derivation of Thomas Precession (by Robert Littlejohn)
- Short derivation of the Thomas precession
 |


