Salem number
In mathematics, a Salem number is a real algebraic integer [math]\displaystyle{ \alpha \gt 1 }[/math] whose conjugate roots all have absolute value no greater than 1, and at least one of which has absolute value exactly 1. Salem numbers are of interest in Diophantine approximation and harmonic analysis. They are named after Raphaël Salem.
Properties
Because it has a root of absolute value 1, the minimal polynomial for a Salem number must be reciprocal. This implies that [math]\displaystyle{ 1/\alpha }[/math] is also a root, and that all other roots have absolute value exactly one. As a consequence α must be a unit in the ring of algebraic integers, being of norm 1.
Every Salem number is a Perron number (a real algebraic number greater than one all of whose conjugates have smaller absolute value).
Relation with Pisot–Vijayaraghavan numbers
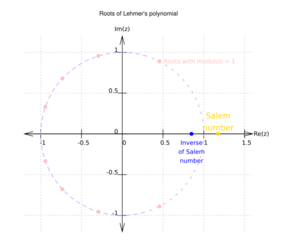
The smallest known Salem number is the largest real root of Lehmer's polynomial (named after Derrick Henry Lehmer)
- [math]\displaystyle{ P(x) = x^{10} + x^9 -x^7 -x^6 -x^5 -x^4 -x^3 +x +1, }[/math]
which is about [math]\displaystyle{ x = 1.17628 }[/math]: it is conjectured that it is indeed the smallest Salem number, and the smallest possible Mahler measure of an irreducible non-cyclotomic polynomial.[1]
Lehmer's polynomial is a factor of the shorter 12th-degree polynomial,
- [math]\displaystyle{ Q(x) = x^{12} - x^7 - x^6 - x^5 + 1, }[/math]
all twelve roots of which satisfy the relation[2]
- [math]\displaystyle{ x^{630}-1 = \frac{(x^{315}-1)(x^{210}-1)(x^{126}-1)^2(x^{90}-1)(x^{3}-1)^3(x^{2}-1)^5(x-1)^3 }{(x^{35}-1)(x^{15}-1)^2(x^{14}-1)^2(x^{5}-1)^6\,x^{68}} }[/math]
Salem numbers can be constructed from Pisot–Vijayaraghavan numbers. To recall, the smallest of the latter is the unique real root of the cubic polynomial,
- [math]\displaystyle{ x^3 - x - 1, }[/math]
known as the plastic ratio and approximately equal to 1.324718. This can be used to generate a family of Salem numbers including the smallest one found so far. The general approach is to take the minimal polynomial [math]\displaystyle{ P(x) }[/math] of a Pisot–Vijayaraghavan number and its reciprocal polynomial, [math]\displaystyle{ P^*(x) }[/math], and solve the equation,
- [math]\displaystyle{ x^n P(x) = \pm P^{*}(x) \, }[/math]
for integral [math]\displaystyle{ n }[/math] above a bound. Subtracting one side from the other, factoring, and disregarding trivial factors will then yield the minimal polynomial of certain Salem numbers. For example, using the negative case of the above,
- [math]\displaystyle{ x^n(x^3-x-1) = -(x^3+x^2-1) }[/math]
then for [math]\displaystyle{ n=8 }[/math], this factors as,
- [math]\displaystyle{ (x-1)(x^{10} + x^9 -x^7 -x^6 -x^5 -x^4 -x^3 +x +1) = 0 }[/math]
where the decic is Lehmer's polynomial. Using higher [math]\displaystyle{ n }[/math] will yield a family with a root approaching the plastic ratio. This can be better understood by taking [math]\displaystyle{ n }[/math]th roots of both sides,
- [math]\displaystyle{ x(x^3-x-1)^{1/n} = \pm (x^3+x^2-1)^{1/n} }[/math]
so as [math]\displaystyle{ n }[/math] goes higher, [math]\displaystyle{ x }[/math] will approach the solution of [math]\displaystyle{ x^3-x-1=0 }[/math]. If the positive case is used, then [math]\displaystyle{ x }[/math] approaches the plastic ratio from the opposite direction. Using the minimal polynomial of the next smallest Pisot–Vijayaraghavan number gives,
- [math]\displaystyle{ x^n (x^4-x^3-1) = -(x^4+x-1) }[/math]
which for [math]\displaystyle{ n=7 }[/math] factors as,
- [math]\displaystyle{ (x-1)(x^{10} -x^6 -x^5 -x^4 +1) = 0 }[/math]
a decic not generated in the previous and has the root [math]\displaystyle{ x=1.216391\ldots }[/math] which is the 5th smallest known Salem number. As [math]\displaystyle{ n\to\infty }[/math], this family in turn tends towards the larger real root of [math]\displaystyle{ x^4-x^3-1=0 }[/math].
References
- ↑ Borwein (2002) p.16
- ↑ D. Bailey and D. Broadhurst, A Seventeenth Order Polylogarithm Ladder
- Borwein, Peter (2002). Computational Excursions in Analysis and Number Theory. CMS Books in Mathematics. Springer-Verlag. ISBN 0-387-95444-9. Chap. 3.
- Hazewinkel, Michiel, ed. (2001), "Salem number", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=s/s120010
- M.J. Mossinghoff. "Small Salem numbers". http://www.cecm.sfu.ca/~mjm/Lehmer/lists/SalemList.html. Retrieved 2016-01-07.
- Salem, R. (1963). Algebraic numbers and Fourier analysis. Heath mathematical monographs. Boston, MA: D. C. Heath and Company.
 |  |
