Scalar projection

If 0° ≤ θ ≤ 90°, as in this case, the scalar projection of a on b coincides with the length of the vector projection.

Vector projection of a on b (a₁), and vector rejection of a from b (a₂).

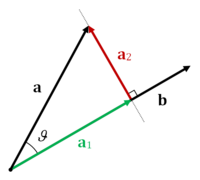
In mathematics, the scalar projection of a vector $\mathbf{𝐚}$ on (or onto) a vector $\mathbf{𝐛}$, also known as the scalar resolute of $\mathbf{𝐚}$ in the direction of $\mathbf{𝐛}$, is given by:

$s=\Vert \mathbf{𝐚}\Vert \cos \theta =\mathbf{𝐚}\cdot \hat{\mathbf{b}},$

where the operator $\cdot$ denotes a dot product, $\widehat{\mathbf{𝐛}}$ is the unit vector in the direction of $\mathbf{𝐛}$, $\Vert \mathbf{𝐚}\Vert$ is the length of $\mathbf{𝐚}$, and $\theta$ is the angle between $\mathbf{𝐚}$ and $\mathbf{𝐛}$.

The term scalar component refers sometimes to scalar projection, as, in Cartesian coordinates, the components of a vector are the scalar projections in the directions of the coordinate axes.

The scalar projection is a scalar, equal to the length of the orthogonal projection of $\mathbf{𝐚}$ on $\mathbf{𝐛}$, with a negative sign if the projection has an opposite direction with respect to $\mathbf{𝐛}$.

Multiplying the scalar projection of $\mathbf{𝐚}$ on $\mathbf{𝐛}$ by $\hat{\mathbf{b}}$ converts it into the above-mentioned orthogonal projection, also called vector projection of $\mathbf{𝐚}$ on $\mathbf{𝐛}$.

Definition based on angle θ

If the angle $\theta$ between $\mathbf{𝐚}$ and $\mathbf{𝐛}$ is known, the scalar projection of $\mathbf{𝐚}$ on $\mathbf{𝐛}$ can be computed using

$s=\Vert \mathbf{𝐚}\Vert \cos \theta .$ ($s=\Vert {\mathbf{𝐚}}_1\Vert$ in the figure)

Definition in terms of a and b

When $\theta$ is not known, the cosine of $\theta$ can be computed in terms of $\mathbf{𝐚}$ and $\mathbf{𝐛}$, by the following property of the dot product $\mathbf{𝐚}\cdot \mathbf{𝐛}$:

$\frac{\mathbf{𝐚}\cdot \mathbf{𝐛}}{\Vert \mathbf{𝐚}\Vert \Vert \mathbf{𝐛}\Vert }=\cos \theta$

By this property, the definition of the scalar projection $s$ becomes:

$s=\Vert {\mathbf{𝐚}}_1\Vert =\Vert \mathbf{𝐚}\Vert \cos \theta =\Vert \mathbf{𝐚}\Vert \frac{\mathbf{𝐚}\cdot \mathbf{𝐛}}{\Vert \mathbf{𝐚}\Vert \Vert \mathbf{𝐛}\Vert }=\frac{\mathbf{𝐚}\cdot \mathbf{𝐛}}{\Vert \mathbf{𝐛}\Vert }$

Properties

The scalar projection has a negative sign if $90<\theta \le 180$ degrees. It coincides with the length of the corresponding vector projection if the angle is smaller than 90°. More exactly, if the vector projection is denoted ${\mathbf{𝐚}}_1$ and its length $\Vert {\mathbf{𝐚}}_1\Vert$:

$s=\Vert {\mathbf{𝐚}}_1\Vert$ if $0<\theta \le 90$ degrees,

$s=-\Vert {\mathbf{𝐚}}_1\Vert$ if $90<\theta \le 180$ degrees.

See also

• Scalar product
• Cross product
• Vector projection