Shearlet

In applied mathematical analysis, shearlets are a multiscale framework which allows efficient encoding of anisotropic features in multivariate problem classes. Originally, shearlets were introduced in 2006 for the analysis and sparse approximation of functions [math]\displaystyle{ f \in L^2(\R^2) }[/math]. They are a natural extension of wavelets, to accommodate the fact that multivariate functions are typically governed by anisotropic features such as edges in images, since wavelets, as isotropic objects, are not capable of capturing such phenomena. Shearlets are constructed by parabolic scaling, shearing, and translation applied to a few generating functions. At fine scales, they are essentially supported within skinny and directional ridges following the parabolic scaling law, which reads length² ≈ width. Similar to wavelets, shearlets arise from the affine group and allow a unified treatment of the continuum and digital situation leading to faithful implementations. Although they do not constitute an orthonormal basis for [math]\displaystyle{ L^2(\R^2) }[/math], they still form a frame allowing stable expansions of arbitrary functions [math]\displaystyle{ f \in L^2(\R^2) }[/math].

One of the most important properties of shearlets is their ability to provide optimally sparse approximations (in the sense of optimality in ) for cartoon-like functions [math]\displaystyle{ f }[/math]. In imaging sciences, cartoon-like functions serve as a model for anisotropic features and are compactly supported in [math]\displaystyle{ [0,1]^2 }[/math] while being [math]\displaystyle{ C^2 }[/math] apart from a closed piecewise [math]\displaystyle{ C^2 }[/math] singularity curve with bounded curvature. The decay rate of the [math]\displaystyle{ L^2 }[/math]-error of the [math]\displaystyle{ N }[/math]-term shearlet approximation obtained by taking the [math]\displaystyle{ N }[/math] largest coefficients from the shearlet expansion is in fact optimal up to a log-factor:

[math]\displaystyle{ \| f - f_N \|_{L^2}^2 \leq C N^{-2} (\log N)^3, \quad N \to \infty, }[/math]

where the constant [math]\displaystyle{ C }[/math] depends only on the maximum curvature of the singularity curve and the maximum magnitudes of [math]\displaystyle{ f }[/math], [math]\displaystyle{ f' }[/math] and [math]\displaystyle{ f'' }[/math]. This approximation rate significantly improves the best [math]\displaystyle{ N }[/math]-term approximation rate of wavelets providing only [math]\displaystyle{ O(N^{-1}) }[/math] for such class of functions.

Shearlets are to date the only directional representation system that provides sparse approximation of anisotropic features while providing a unified treatment of the continuum and digital realm that allows faithful implementation. Extensions of shearlet systems to [math]\displaystyle{ L^2(\R^d), d \ge 2 }[/math] are also available. A comprehensive presentation of the theory and applications of shearlets can be found in.

Definition

Continuous shearlet systems

Geometric effects of parabolic scaling and shearing with several parameters a and s.

The construction of continuous shearlet systems is based on parabolic scaling matrices

[math]\displaystyle{ A_a = \begin{bmatrix} a & 0 \\ 0 & a^{1/2} \end{bmatrix}, \quad a \gt 0 }[/math]

as a mean to change the resolution, on shear matrices

[math]\displaystyle{ S_s = \begin{bmatrix} 1 & s \\ 0 & 1 \end{bmatrix}, \quad s \in \R }[/math]

as a means to change the orientation, and finally on translations to change the positioning. In comparison to curvelets, shearlets use shearings instead of rotations, the advantage being that the shear operator [math]\displaystyle{ S_s }[/math] leaves the integer lattice invariant in case [math]\displaystyle{ s \in \Z }[/math], i.e., [math]\displaystyle{ S_s \Z^2 \subseteq \Z^2. }[/math] This indeed allows a unified treatment of the continuum and digital realm, thereby guaranteeing a faithful digital implementation.

For [math]\displaystyle{ \psi \in L^2(\R^2) }[/math] the continuous shearlet system generated by [math]\displaystyle{ \psi }[/math] is then defined as

[math]\displaystyle{ \operatorname{SH}_{\mathrm{cont}}(\psi) = \{ \psi_{a,s,t} = a^{3/4} \psi(S_s A_a (\cdot - t)) \mid a \gt 0, s \in \R, t \in \R^2 \}, }[/math]

and the corresponding continuous shearlet transform is given by the map

[math]\displaystyle{ f \mapsto \mathcal{SH}_\psi f(a, s, t) = \langle f, \psi_{a,s,t} \rangle, \quad f \in L^2(\R^2), \quad (a, s, t) \in \R_{\gt 0} \times \R \times \R^2. }[/math]

Discrete shearlet systems

A discrete version of shearlet systems can be directly obtained from [math]\displaystyle{ \operatorname{SH}_{\mathrm{cont}}(\psi) }[/math] by discretizing the parameter set [math]\displaystyle{ \R_{\gt 0} \times \R \times \R^2. }[/math] There are numerous approaches for this but the most popular one is given by

[math]\displaystyle{ \{ (2^j, k, A_{2^j}^{-1} S_k^{-1} m) \mid j \in \Z, k \in \Z, m \in \Z^2\} \subseteq \R_{\gt 0} \times \R \times \R^2. }[/math]

From this, the discrete shearlet system associated with the shearlet generator [math]\displaystyle{ \psi }[/math] is defined by

[math]\displaystyle{ \operatorname{SH}(\psi) = \{ \psi_{j,k,m} = 2^{3j/4} \psi(S_k A_{2^j} \cdot{} - m) \mid j \in \Z, k \in \Z, m \in \Z^2 \}, }[/math]

and the associated discrete shearlet transform is defined by

[math]\displaystyle{ f \mapsto \mathcal{SH}_\psi f(j, k, m) = \langle f, \psi_{j,k,m} \rangle, \quad f \in L^2(\R^2), \quad (j, k, m) \in \Z \times \Z \times \Z^2. }[/math]

Examples

Trapezoidal frequency support of the classical shearlet.

Frequency tiling of the (discrete) classical shearlet system.

Let [math]\displaystyle{ \psi_1 \in L^2(\R) }[/math] be a function satisfying the discrete Calderón condition, i.e.,

[math]\displaystyle{ \sum_{j \in \Z} |\hat\psi_1(2^{-j} \xi)|^2 = 1, \text{for a.e. } \xi \in \R, }[/math]

with [math]\displaystyle{ \hat\psi_1 \in C^\infty(\R) }[/math] and [math]\displaystyle{ \operatorname{supp}\hat\psi_1 \subseteq [-\tfrac{1}{2}, -\tfrac{1}{16}] \cup [\tfrac{1}{16}, \tfrac{1}{2}], }[/math] where [math]\displaystyle{ \hat\psi_1 }[/math] denotes the Fourier transform of [math]\displaystyle{ \psi_1. }[/math] For instance, one can choose [math]\displaystyle{ \psi_1 }[/math] to be a Meyer wavelet. Furthermore, let [math]\displaystyle{ \psi_2 \in L^2(\R) }[/math] be such that [math]\displaystyle{ \hat\psi_2 \in C^\infty(\R), }[/math] [math]\displaystyle{ \operatorname{supp}\hat\psi_2 \subseteq [-1, 1] }[/math] and

[math]\displaystyle{ \sum_{k= -1}^{1} |\hat\psi_2(\xi + k)|^2 = 1, \text{for a.e. } \xi\in\left[-1, 1\right]. }[/math]

One typically chooses [math]\displaystyle{ \hat \psi_2 }[/math] to be a smooth bump function. Then [math]\displaystyle{ \psi \in L^2(\R^2) }[/math] given by

[math]\displaystyle{ \hat\psi(\xi) = \hat\psi_1(\xi_1) \hat\psi_2\left( \tfrac{\xi_2}{\xi_1} \right), \quad \xi = (\xi_1, \xi_2) \in \R^2, }[/math]

is called a classical shearlet. It can be shown that the corresponding discrete shearlet system [math]\displaystyle{ \operatorname{SH}(\psi) }[/math] constitutes a Parseval frame for [math]\displaystyle{ L^2(\R^2) }[/math] consisting of bandlimited functions.

Another example are compactly supported shearlet systems, where a compactly supported function [math]\displaystyle{ \psi \in L^2(\R^2) }[/math] can be chosen so that [math]\displaystyle{ \operatorname{SH}(\psi) }[/math] forms a frame for [math]\displaystyle{ L^2(\R^2) }[/math]. In this case, all shearlet elements in [math]\displaystyle{ \operatorname{SH}(\psi) }[/math] are compactly supported providing superior spatial localization compared to the classical shearlets, which are bandlimited. Although a compactly supported shearlet system does not generally form a Parseval frame, any function [math]\displaystyle{ f \in L^2(\R^2) }[/math] can be represented by the shearlet expansion due to its frame property.

Cone-adapted shearlets

One drawback of shearlets defined as above is the directional bias of shearlet elements associated with large shearing parameters. This effect is already recognizable in the frequency tiling of classical shearlets (see Figure in Section #Examples), where the frequency support of a shearlet increasingly aligns along the [math]\displaystyle{ \xi_2 }[/math]-axis as the shearing parameter [math]\displaystyle{ s }[/math] goes to infinity. This causes serious problems when analyzing a function whose Fourier transform is concentrated around the [math]\displaystyle{ \xi_2 }[/math]-axis.

Decomposition of the frequency domain into cones.

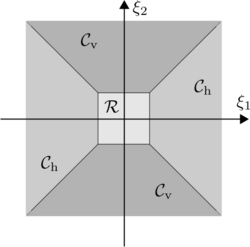
To deal with this problem, the frequency domain is divided into a low-frequency part and two conic regions (see Figure):

[math]\displaystyle{ \begin{align} \mathcal{R} &= \left\{ (\xi_1, \xi_2) \in \R^2 \mid |\xi_1|, |\xi_2| \leq 1 \right\}, \\ \mathcal{C}_{\mathrm{h}} &= \left\{ (\xi_1, \xi_2) \in \R^2 \mid | \xi_2 / \xi_1 | \leq 1, |\xi_1| \gt 1 \right\}, \\ \mathcal{C}_{\mathrm{v}} &= \left\{ (\xi_1, \xi_2) \in \R^2 \mid | \xi_1 / \xi_2 | \leq 1, |\xi_2| \gt 1 \right\}. \end{align} }[/math]

Frequency tiling of the cone-adapted shearlet system generated by the classical shearlet.

The associated cone-adapted discrete shearlet system consists of three parts, each one corresponding to one of these frequency domains. It is generated by three functions [math]\displaystyle{ \phi, \psi, \tilde\psi \in L^2(\R^2) }[/math] and a lattice sampling factor [math]\displaystyle{ c = (c_1, c_2) \in (\R_{\gt 0})^2: }[/math]

[math]\displaystyle{ \operatorname{SH}(\phi, \psi, \tilde\psi; c) = \Phi(\phi; c_1) \cup \Psi(\psi; c) \cup \tilde\Psi(\tilde\psi; c), }[/math]

where

[math]\displaystyle{ \begin{align} \Phi(\phi; c_1) &= \{ \phi_m = \phi(\cdot{} - c_1 m) \mid m \in \Z^2 \}, \\ \Psi(\psi; c) &= \{ \psi_{j,k,m} = 2^{3j/4} \psi(S_k A_{2^j} \cdot{} - M_c m) \mid j \geq 0, |k| \leq \lceil 2^{j/2} \rceil, m \in \Z^2 \}, \\ \tilde\Psi(\tilde\psi; c) &= \{ \tilde{\psi}_{j,k,m} = 2^{3j/4} \psi(\tilde{S}_k \tilde{A}_{2^j} \cdot{} - \tilde{M}_c m) \mid j \geq 0, |k| \leq \lceil 2^{j/2} \rceil, m \in \Z^2 \}, \end{align} }[/math]

with

[math]\displaystyle{ \begin{align} & \tilde{A}_a = \begin{bmatrix} a^{1/2} & 0 \\ 0 & a \end{bmatrix}, \; a \gt 0, \quad \tilde{S}_s = \begin{bmatrix} 1 & 0 \\ s & 1 \end{bmatrix}, \; s \in \R, \quad M_c = \begin{bmatrix} c_1 & 0 \\ 0 & c_2 \end{bmatrix}, \quad \text{and} \quad \tilde{M}_c = \begin{bmatrix} c_2 & 0 \\ 0 & c_1 \end{bmatrix}. \end{align} }[/math]

The systems [math]\displaystyle{ \Psi(\psi) }[/math] and [math]\displaystyle{ \tilde\Psi(\tilde\psi) }[/math] basically differ in the reversed roles of [math]\displaystyle{ x_1 }[/math] and [math]\displaystyle{ x_2 }[/math]. Thus, they correspond to the conic regions [math]\displaystyle{ \mathcal{C}_{\mathrm{h}} }[/math] and [math]\displaystyle{ \mathcal{C}_{\mathrm{v}} }[/math], respectively. Finally, the scaling function [math]\displaystyle{ \phi }[/math] is associated with the low-frequency part [math]\displaystyle{ \mathcal{R} }[/math].

Applications

• Image processing and computer sciences
  • Denoising
  • Inverse problems
  • Image enhancement
  • Edge detection
  • Inpainting
  • Image separation
• PDEs
  • Resolution of the wavefront set
  • Transport equations
• Coorbit theory, characterization of smoothness spaces
• Differential geometry: manifold learning

Generalizations and extensions

• 3D-Shearlets
• [math]\displaystyle{ \alpha }[/math]-Shearlets
• Parabolic molecules
• Cylindrical Shearlets

See also

• Wavelet transform
• Curvelet transform
• Contourlet transform
• Bandelet transform
• Chirplet transform
• Noiselet transform

External links

• Homepage of Gitta Kutyniok
• Homepage of Demetrio Labate