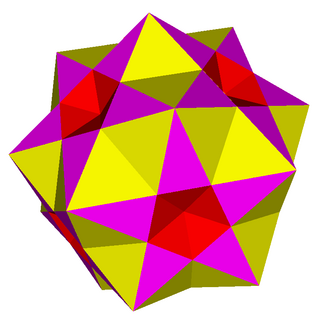
Small complex rhombicosidodecahedron
| Small complex rhombicosidodecahedron | |
|---|---|
| |
| Type | Uniform star polyhedron |
| Elements | F = 62, E = 120 (60x2) V = 20 (χ = -38) |
| Faces by sides | 20{3}+12{5/2}+30{4} |
| Wythoff symbol | 5/2 3 | 2 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U-, C-, W- |
| Dual polyhedron | Small complex rhombicosidodecacron |
| Vertex figure |  3(3.4.5/2.4) |
| Bowers acronym | Sicdatrid |
In geometry, the small complex rhombicosidodecahedron (also known as the small complex ditrigonal rhombicosidodecahedron) is a degenerate uniform star polyhedron. It has 62 faces (20 triangles, 12 pentagrams and 30 squares), 120 (doubled) edges and 20 vertices. All edges are doubled (making it degenerate), sharing 4 faces, but are considered as two overlapping edges as a topological polyhedron.
It can be constructed from the vertex figure 3(5/2.4.3.4), thus making it also a cantellated great icosahedron. The "3" in front of this vertex figure indicates that each vertex in this degenerate polyhedron is in fact three coincident vertices. It may also be given the Schläfli symbol rr{5⁄2,3} or t0,2{5⁄2,3}.
As a compound
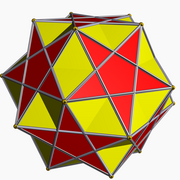
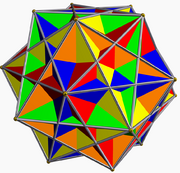
It can be seen as a compound of the small ditrigonal icosidodecahedron, U30, and the compound of five cubes. It is also a faceting of the dodecahedron.
|
|

|
| Small ditrigonal icosidodecahedron | Compound of five cubes | Compound |
As a cantellation
It can also be seen as a cantellation of the great icosahedron (or, equivalently, of the great stellated dodecahedron).
| (p q 2) | Fund. triangle |
Parent | Truncated | Rectified | Bitruncated | Birectified (dual) |
Cantellated | Omnitruncated (Cantitruncated) |
Snub |
|---|---|---|---|---|---|---|---|---|---|
| Wythoff symbol | q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Schläfli symbol | t0{p,q} | t0,1{p,q} | t1{p,q} | t1,2{p,q} | t2{p,q} | t0,2{p,q} | t0,1,2{p,q} | s{p,q} | |
| Coxeter–Dynkin diagram | |||||||||
| Vertex figure | pq | q.2p.2p | p.q.p.q | p.2q.2q | qp | p.4.q.4 | 4.2p.2q | 3.3.p.3.q | |
| Icosahedral (5⁄2 3 2) |
 {3,5⁄2} |
 5⁄2.6.6 |
 (3.5⁄2)2 |
 3.10⁄2.10⁄2 |
 {5⁄2,3} |
 3.4.5⁄2.4 |
 4.10⁄2.6 |
 3.3.3.3.5⁄2 |
Related degenerate uniform polyhedra
Two other degenerate uniform polyhedra are also facettings of the dodecahedron. They are the complex rhombidodecadodecahedron (a compound of the ditrigonal dodecadodecahedron and the compound of five cubes) with vertex figure (5⁄3.4.5.4)/3 and the great complex rhombicosidodecahedron (a compound of the great ditrigonal icosidodecahedron and the compound of five cubes) with vertex figure (5⁄4.4.3⁄2.4)/3. All three degenerate uniform polyhedra have each vertex in fact being three coincident vertices and each edge in fact being two coincident edges.
They can all be constructed by cantellation of regular polyhedra. The complex rhombidodecadodecahedron may be given the Schläfli symbol rr{5⁄3,5} or t0,2{5⁄3,5}, while the great complex rhombicosidodecahedron may be given the Schläfli symbol rr{5⁄4,3⁄2} or t0,2{5⁄4,3⁄2}.
| Cantellated polyhedron | 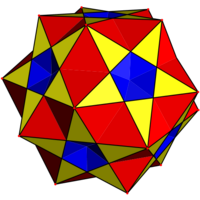 Small complex rhombicosidodecahedron |
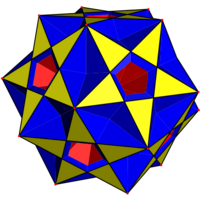 Complex rhombidodecadodecahedron |
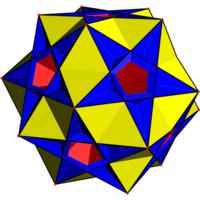 Great complex rhombicosidodecahedron | |||
|---|---|---|---|---|---|---|
| Related polyhedron |  Great icosahedron |
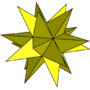 Great stellated dodecahedron |
 Great dodecahedron |
 Small stellated dodecahedron |
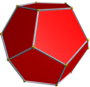 Regular dodecahedron |
 Regular icosahedron |
See also
- Small complex icosidodecahedron
- Great complex icosidodecahedron
- Complex rhombidodecadodecahedron
- Great complex rhombicosidodecahedron
References
- Klitzing, Richard. "3D uniform polyhedra sicdatrid". https://bendwavy.org/klitzing/dimensions/polyhedra-neu.htm.
- Klitzing, Richard. "3D uniform polyhedra cadditradid". https://bendwavy.org/klitzing/dimensions/polyhedra-neu.htm.
- Klitzing, Richard. "3D uniform polyhedra gicdatrid". https://bendwavy.org/klitzing/dimensions/polyhedra-neu.htm.

