Smooth maximum
In mathematics, a smooth maximum of an indexed family x1, ..., xn of numbers is a smooth approximation to the maximum function [math]\displaystyle{ \max(x_1,\ldots,x_n), }[/math] meaning a parametric family of functions [math]\displaystyle{ m_\alpha(x_1,\ldots,x_n) }[/math] such that for every α, the function [math]\displaystyle{ m_\alpha }[/math] is smooth, and the family converges to the maximum function [math]\displaystyle{ m_\alpha \to \max }[/math] as [math]\displaystyle{ \alpha\to\infty }[/math]. The concept of smooth minimum is similarly defined. In many cases, a single family approximates both: maximum as the parameter goes to positive infinity, minimum as the parameter goes to negative infinity; in symbols, [math]\displaystyle{ m_\alpha \to \max }[/math] as [math]\displaystyle{ \alpha \to \infty }[/math] and [math]\displaystyle{ m_\alpha \to \min }[/math] as [math]\displaystyle{ \alpha \to -\infty }[/math]. The term can also be used loosely for a specific smooth function that behaves similarly to a maximum, without necessarily being part of a parametrized family.
Examples
Boltzmann operator
For large positive values of the parameter [math]\displaystyle{ \alpha \gt 0 }[/math], the following formulation is a smooth, differentiable approximation of the maximum function. For negative values of the parameter that are large in absolute value, it approximates the minimum.
- [math]\displaystyle{ \mathcal{S}_\alpha (x_1,\ldots,x_n) = \frac{\sum_{i=1}^n x_i e^{\alpha x_i}}{\sum_{i=1}^n e^{\alpha x_i}} }[/math]
[math]\displaystyle{ \mathcal{S}_\alpha }[/math] has the following properties:
- [math]\displaystyle{ \mathcal{S}_\alpha\to \max }[/math] as [math]\displaystyle{ \alpha\to\infty }[/math]
- [math]\displaystyle{ \mathcal{S}_0 }[/math] is the arithmetic mean of its inputs
- [math]\displaystyle{ \mathcal{S}_\alpha\to \min }[/math] as [math]\displaystyle{ \alpha\to -\infty }[/math]
The gradient of [math]\displaystyle{ \mathcal{S}_{\alpha} }[/math] is closely related to softmax and is given by
- [math]\displaystyle{ \nabla_{x_i}\mathcal{S}_\alpha (x_1,\ldots,x_n) = \frac{e^{\alpha x_i}}{\sum_{j=1}^n e^{\alpha x_j}} [1 + \alpha(x_i - \mathcal{S}_\alpha (x_1,\ldots,x_n))]. }[/math]
This makes the softmax function useful for optimization techniques that use gradient descent.
This operator is sometimes called the Boltzmann operator,[1] after the Boltzmann distribution.
LogSumExp
Another smooth maximum is LogSumExp:
- [math]\displaystyle{ \mathrm{LSE}_\alpha(x_1, \ldots, x_n) = \frac{1}{\alpha} \log \sum_{i=1}^n \exp \alpha x_i }[/math]
This can also be normalized if the [math]\displaystyle{ x_i }[/math] are all non-negative, yielding a function with domain [math]\displaystyle{ [0,\infty)^n }[/math] and range [math]\displaystyle{ [0, \infty) }[/math]:
- [math]\displaystyle{ g(x_1, \ldots, x_n) = \log \left( \sum_{i=1}^n \exp x_i - (n-1) \right) }[/math]
The [math]\displaystyle{ (n - 1) }[/math] term corrects for the fact that [math]\displaystyle{ \exp(0) = 1 }[/math] by canceling out all but one zero exponential, and [math]\displaystyle{ \log 1 = 0 }[/math] if all [math]\displaystyle{ x_i }[/math] are zero.
Mellowmax
The mellowmax operator[1] is defined as follows:
- [math]\displaystyle{ \mathrm{mm}_\alpha(x) = \frac{1}{\alpha} \log \frac{1}{n} \sum_{i=1}^n \exp \alpha x_i }[/math]
It is a non-expansive operator. As [math]\displaystyle{ \alpha \to \infty }[/math], it acts like a maximum. As [math]\displaystyle{ \alpha \to 0 }[/math], it acts like an arithmetic mean. As [math]\displaystyle{ \alpha \to -\infty }[/math], it acts like a minimum. This operator can be viewed as a particular instantiation of the quasi-arithmetic mean. It can also be derived from information theoretical principles as a way of regularizing policies with a cost function defined by KL divergence. The operator has previously been utilized in other areas, such as power engineering.[2]
p-Norm
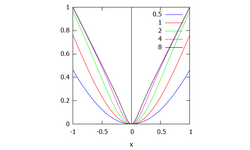
Another smooth maximum is the p-norm:
- [math]\displaystyle{ \| (x_1, \ldots, x_n) \|_p = \left( \sum_{i=1}^n |x_i|^p \right)^\frac{1}{p} }[/math]
which converges to [math]\displaystyle{ \| (x_1, \ldots, x_n) \|_\infty = \max_{1\leq i\leq n} |x_i| }[/math] as [math]\displaystyle{ p \to \infty }[/math].
An advantage of the p-norm is that it is a norm. As such it is scale invariant (homogeneous): [math]\displaystyle{ \| (\lambda x_1, \ldots, \lambda x_n) \|_p = |\lambda| \cdot \| (x_1, \ldots, x_n) \|_p }[/math], and it satisfies the triangle inequality.
Smooth maximum unit
The following binary operator is called the Smooth Maximum Unit (SMU):[3]
- [math]\displaystyle{ \begin{align} \textstyle\max_\varepsilon(a, b) &= \frac{a + b + |a - b|_\varepsilon}{2} \\ &= \frac{a + b + \sqrt{(a - b)^2 + \varepsilon}}{2} \end{align} }[/math]
where [math]\displaystyle{ \varepsilon \geq 0 }[/math] is a parameter. As [math]\displaystyle{ \varepsilon \to 0 }[/math], [math]\displaystyle{ |\cdot|_\varepsilon \to |\cdot| }[/math] and thus [math]\displaystyle{ \textstyle\max_\varepsilon \to \max }[/math].
See also
References
- ↑ 1.0 1.1 Asadi, Kavosh; Littman, Michael L. (2017). "An Alternative Softmax Operator for Reinforcement Learning". PMLR 70: 243–252. https://proceedings.mlr.press/v70/asadi17a.html. Retrieved January 6, 2023.
- ↑ Safak, Aysel (February 1993). "Statistical analysis of the power sum of multiple correlated log-normal components". IEEE Transactions on Vehicular Technology 42 (1): {58–61. doi:10.1109/25.192387. https://ieeexplore.ieee.org/document/192387. Retrieved January 6, 2023.
- ↑ Biswas, Koushik; Kumar, Sandeep; Banerjee, Shilpak; Ashish Kumar Pandey (2021). "SMU: Smooth activation function for deep networks using smoothing maximum technique". arXiv:2111.04682 [cs.LG].
https://www.johndcook.com/soft_maximum.pdf
M. Lange, D. Zühlke, O. Holz, and T. Villmann, "Applications of lp-norms and their smooth approximations for gradient based learning vector quantization," in Proc. ESANN, Apr. 2014, pp. 271-276. (https://www.elen.ucl.ac.be/Proceedings/esann/esannpdf/es2014-153.pdf)
 |  |
