Van 't Hoff factor
The van 't Hoff factor i (named after Dutch chemist Jacobus Henricus van 't Hoff) is a measure of the effect of a solute on colligative properties such as osmotic pressure, relative lowering in vapor pressure, boiling-point elevation and freezing-point depression. The van 't Hoff factor is the ratio between the actual concentration of particles produced when the substance is dissolved and the concentration of a substance as calculated from its mass. For most non-electrolytes dissolved in water, the van 't Hoff factor is essentially 1.
For most ionic compounds dissolved in water, the van 't Hoff factor is equal to the number of discrete ions in a formula unit of the substance. This is true for ideal solutions only, as occasionally ion pairing occurs in solution. At a given instant a small percentage of the ions are paired and count as a single particle. Ion pairing occurs to some extent in all electrolyte solutions. This causes the measured van 't Hoff factor to be less than that predicted in an ideal solution. The deviation for the van 't Hoff factor tends to be greatest where the ions have multiple charges.
The factor binds osmolarity to molarity and osmolality to molality.
Dissociated solutes
The degree of dissociation is the fraction of the original solute molecules that have dissociated. It is usually indicated by the Greek symbol [math]\displaystyle{ \alpha }[/math]. There is a simple relationship between this parameter and the van 't Hoff factor. If a fraction [math]\displaystyle{ \alpha }[/math] of the solute dissociates into [math]\displaystyle{ n }[/math] ions, then
- [math]\displaystyle{ i = 1 + \alpha (n - 1). }[/math]
For example, the dissociation KCl ⇌ K+ + Cl− yields [math]\displaystyle{ n = 2 }[/math] ions, so that [math]\displaystyle{ i = 1 + \alpha }[/math].
For dissociation in the absence of association, the van 't Hoff factor is: [math]\displaystyle{ i \gt 1 }[/math].
Associated solutes
Similarly, if a fraction [math]\displaystyle{ \alpha }[/math] of [math]\displaystyle{ n }[/math] moles of solute associate to form one mole of an n-mer (dimer, trimer, etc.), then
- [math]\displaystyle{ i = 1 - \left(1 - \frac{1}{n}\right)\alpha. }[/math]
For the dimerisation of acetic acid in benzene:
- 2 CH3COOH ⇌ (CH3COOH)2
2 moles of acetic acid associate to form 1 mole of dimer, so that
- [math]\displaystyle{ i = 1 - \left(1 - \frac{1}{2}\right)\alpha = 1 - \frac{\alpha}{2}. }[/math]
For association in the absence of dissociation, the van 't Hoff factor is: [math]\displaystyle{ i \lt 1 }[/math].
Physical significance of i
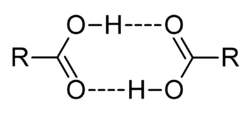
- When solute particles associate in solution, i is less than 1. For example, carboxylic acids such as acetic acid (ethanoic acid) or benzoic acid form dimers in benzene, so that the number of solute particles is half the number of acid molecules.
- When solute particles dissociate in solution, i is greater than 1 (e.g. sodium chloride in water, potassium chloride in water, magnesium chloride in water).
- When solute particles neither dissociate nor associate in solution, i equals 1 (e.g. glucose in water).
The value of i is the actual number of particles in solution after dissociation divided by the number of formula units initially dissolved in solution and means the number of particles per formula unit of the solute when a solution is dilute.
Relation to osmotic coefficient
This quantity can be related to the osmotic coefficient g by the relation: [math]\displaystyle{ i = n g }[/math].
See also
- Colligative properties
- Thermodynamic activity
- Raoult's law
- Law of dilution
- Van 't Hoff equation
- Dissociation
- Osmosis
- Osmotic coefficient
References
- Tro, Nivaldo J. (2020). Chemistry : A Molecular Approach (Fifth ed.). Hoboken, NJ. pp. 613–614. ISBN 978-0-13-498889-4. OCLC 1048659501. https://www.worldcat.org/oclc/1048659501.
 |  |
