Physics:Vapor pressure

From HandWiki
Short description: Pressure exerted by a vapor in thermodynamic equilibrium
The microscopic process of evaporation and condensation at the liquid surface.
If vapor pressure exceeds the thermodynamic equilibrium value, condensation occurs in presence of nucleation sites. This principle is indigenous in cloud chambers, where ionized particles form condensation tracks when passing through.

File:02.Пиштол епрувета со алкохол.ogv

Vapor pressure[lower-alpha 1] or equilibrium vapor pressure is the pressure exerted by a vapor in thermodynamic equilibrium with its condensed phases (solid or liquid) at a given temperature in a closed system. The equilibrium vapor pressure is an indication of a liquid's thermodynamic tendency to evaporate. It relates to the balance of particles escaping from the liquid (or solid) in equilibrium with those in a coexisting vapor phase. A substance with a high vapor pressure at normal temperatures is often referred to as volatile. The pressure exhibited by vapor present above a liquid surface is known as vapor pressure. As the temperature of a liquid increases, the attractive interactions between liquid molecules become less significant in comparison to the entropy of those molecules in the gas phase, increasing the vapor pressure. Thus, liquids with strong intermolecular interactions are likely to have smaller vapor pressures, with the reverse true for weaker interactions.

The vapor pressure of any substance increases non-linearly with temperature, often described by the Clausius–Clapeyron relation. The atmospheric pressure boiling point of a liquid (also known as the normal boiling point) is the temperature at which the vapor pressure equals the ambient atmospheric pressure. With any incremental increase in that temperature, the vapor pressure becomes sufficient to overcome atmospheric pressure and cause the liquid to form vapor bubbles. Bubble formation in high liquid depths requires a slightly higher temperature due to the higher fluid pressure, due to hydrostatic pressure of the fluid mass above. More important at shallow depths is the higher temperature required to start bubble formation. The surface tension of the bubble wall leads to an overpressure in the very small, initial bubbles.

The vapor pressure that a single component in a mixture contributes to the total pressure in the system is called partial pressure. For example, air at sea level, and saturated with water vapor at 20 °C, has partial pressures of about 2.3 kPa of water, 78 kPa of nitrogen, 21 kPa of oxygen and 0.9 kPa of argon, totaling 102.2 kPa, making the basis for standard atmospheric pressure.

Measurement and units

Vapor pressure is measured in the standard units of pressure. The International System of Units (SI) recognizes pressure as a derived unit with the dimension of force per area and designates the pascal (Pa) as its standard unit. One pascal is one newton per square meter (N·m−2 or kg·m−1·s−2).

Experimental measurement of vapor pressure is a simple procedure for common pressures between 1 and 200 kPa.[1] Most accurate results are obtained near the boiling point of substances and large errors result for measurements smaller than 1kPa. Procedures often consist of purifying the test substance, isolating it in a container, evacuating any foreign gas, then measuring the equilibrium pressure of the gaseous phase of the substance in the container at different temperatures. Better accuracy is achieved when care is taken to ensure that the entire substance and its vapor are at the prescribed temperature. This is often done, as with the use of an isoteniscope, by submerging the containment area in a liquid bath.

Very low vapor pressures of solids can be measured using the Knudsen effusion cell method.

In a medical context, vapor pressure is sometimes expressed in other units, specifically millimeters of mercury (mmHg). This is important for volatile inhalational anesthetics, most of which are liquids at body temperature, but with a relatively high vapor pressure.

Estimating vapor pressures with Antoine equation

The Antoine equation[2][3] is a pragmatic mathematical expression of the relation between the vapor pressure and the temperature of pure liquid or solid substances. It is obtained by curve-fitting and is adapted to the fact that vapor pressure is usually increasing and concave as a function of temperature. The basic form of the equation is:

[math]\displaystyle{ \log P = A-\frac{B}{C+T} }[/math]

and it can be transformed into this temperature-explicit form:

[math]\displaystyle{ T = \frac{B}{A-\log P} - C }[/math]

where:

  • [math]\displaystyle{ P }[/math] is the absolute vapor pressure of a substance
  • [math]\displaystyle{ T }[/math] is the temperature of the substance
  • [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math] and [math]\displaystyle{ C }[/math] are substance-specific coefficients (i.e., constants or parameters)
  • [math]\displaystyle{ \log }[/math] is typically either [math]\displaystyle{ \log_{10} }[/math] or [math]\displaystyle{ \log_e }[/math][3]

A simpler form of the equation with only two coefficients is sometimes used:

[math]\displaystyle{ \log P = A- \frac{B}{T} }[/math]

which can be transformed to:

[math]\displaystyle{ T = \frac{B}{A-\log P} }[/math]

Sublimations and vaporizations of the same substance have separate sets of Antoine coefficients, as do components in mixtures.[2] Each parameter set for a specific compound is only applicable over a specified temperature range. Generally, temperature ranges are chosen to maintain the equation's accuracy of a few up to 8–10 percent. For many volatile substances, several different sets of parameters are available and used for different temperature ranges. The Antoine equation has poor accuracy with any single parameter set when used from a compound's melting point to its critical temperature. Accuracy is also usually poor when vapor pressure is under 10 Torr because of the limitations of the apparatus[citation needed] used to establish the Antoine parameter values.

The Wagner equation[4] gives "one of the best"[5] fits to experimental data but is quite complex. It expresses reduced vapor pressure as a function of reduced temperature.

Relation to boiling point of liquids

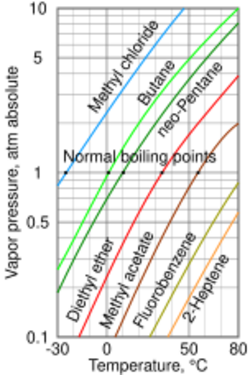
Further information: Physics:Boiling point
A log-lin vapor pressure chart for various liquids

As a general trend, vapor pressures of liquids at ambient temperatures increase with decreasing boiling points. This is illustrated in the vapor pressure chart (see right) that shows graphs of the vapor pressures versus temperatures for a variety of liquids.[6] At the normal boiling point of a liquid, the vapor pressure is equal to the standard atmospheric pressure defined as 1 atmosphere,[7] 760 Torr, 101.325 kPa, or 14.69595 psi.

For example, at any given temperature, methyl chloride has the highest vapor pressure of any of the liquids in the chart. It also has the lowest normal boiling point at −24.2 °C (−11.6 °F), which is where the vapor pressure curve of methyl chloride (the blue line) intersects the horizontal pressure line of one atmosphere (atm) of absolute vapor pressure.

Although the relation between vapor pressure and temperature is non-linear, the chart uses a logarithmic vertical axis to produce slightly curved lines, so one chart can graph many liquids. A nearly straight line is obtained when the logarithm of the vapor pressure is plotted against 1/(T + 230)[8] where T is the temperature in degrees Celsius. The vapor pressure of a liquid at its boiling point equals the pressure of its surrounding environment.

Liquid mixtures: Raoult's law

Raoult's law gives an approximation to the vapor pressure of mixtures of liquids. It states that the activity (pressure or fugacity) of a single-phase mixture is equal to the mole-fraction-weighted sum of the components' vapor pressures:

[math]\displaystyle{ P_{\rm tot} =\sum_i P y_i = \sum_i P_i^{\rm sat} x_i \, }[/math]

where [math]\displaystyle{ P_{\rm tot} }[/math] is the mixture's vapor pressure, [math]\displaystyle{ x_i }[/math] is the mole fraction of component [math]\displaystyle{ i }[/math] in the liquid phase and [math]\displaystyle{ y_i }[/math] is the mole fraction of component [math]\displaystyle{ i }[/math] in the vapor phase respectively. [math]\displaystyle{ P_i^{\rm sat} }[/math] is the vapor pressure of component [math]\displaystyle{ i }[/math]. Raoult's law is applicable only to non-electrolytes (uncharged species); it is most appropriate for non-polar molecules with only weak intermolecular attractions (such as London forces).

Systems that have vapor pressures higher than indicated by the above formula are said to have positive deviations. Such a deviation suggests weaker intermolecular attraction than in the pure components, so that the molecules can be thought of as being "held in" the liquid phase less strongly than in the pure liquid. An example is the azeotrope of approximately 95% ethanol and water. Because the azeotrope's vapor pressure is higher than predicted by Raoult's law, it boils at a temperature below that of either pure component.

There are also systems with negative deviations that have vapor pressures that are lower than expected. Such a deviation is evidence for stronger intermolecular attraction between the constituents of the mixture than exists in the pure components. Thus, the molecules are "held in" the liquid more strongly when a second molecule is present. An example is a mixture of trichloromethane (chloroform) and 2-propanone (acetone), which boils above the boiling point of either pure component.

The negative and positive deviations can be used to determine thermodynamic activity coefficients of the components of mixtures.

Solids

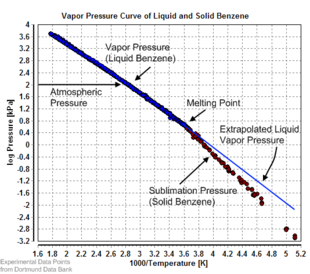
Vapor pressure of liquid and solid benzene

Equilibrium vapor pressure can be defined as the pressure reached when a condensed phase is in equilibrium with its own vapor. In the case of an equilibrium solid, such as a crystal, this can be defined as the pressure when the rate of sublimation of a solid matches the rate of deposition of its vapor phase. For most solids this pressure is very low, but some notable exceptions are naphthalene, dry ice (the vapor pressure of dry ice is 5.73 MPa (831 psi, 56.5 atm) at 20 °C, which causes most sealed containers to rupture), and ice. All solid materials have a vapor pressure. However, due to their often extremely low values, measurement can be rather difficult. Typical techniques include the use of thermogravimetry and gas transpiration.

There are a number of methods for calculating the sublimation pressure (i.e., the vapor pressure) of a solid. One method is to estimate the sublimation pressure from extrapolated liquid vapor pressures (of the supercooled liquid), if the heat of fusion is known, by using this particular form of the Clausius–Clapeyron relation:[9]

[math]\displaystyle{ \ln\,P^{\rm sub}_{\rm s} = \ln\,P^{\rm sub}_{\rm l} - \frac{\Delta_{\rm fus}H}{R} \left( \frac{1}{T_{\rm sub}} - \frac{1}{T_{\rm fus}} \right) }[/math]

where:

  • [math]\displaystyle{ P^{\rm sub}_{\rm s} }[/math] is the sublimation pressure of the solid component at the temperature [math]\displaystyle{ T_{\rm sub} \lt T_{\rm fus} }[/math].
  • [math]\displaystyle{ P^{\rm sub}_{\rm l} }[/math] is the extrapolated vapor pressure of the liquid component at the temperature [math]\displaystyle{ T_{\rm sub} \lt T_{\rm fus} }[/math].
  • [math]\displaystyle{ \Delta_{\rm fus}H }[/math] is the heat of fusion.
  • [math]\displaystyle{ R }[/math] is the gas constant.
  • [math]\displaystyle{ T_{\rm sub} }[/math] is the sublimation temperature.
  • [math]\displaystyle{ T_{\rm fus} }[/math] is the melting point temperature.

This method assumes that the heat of fusion is temperature-independent, ignores additional transition temperatures between different solid phases, and it gives a fair estimation for temperatures not too far from the melting point. It also shows that the sublimation pressure is lower than the extrapolated liquid vapor pressure (ΔfusH > 0) and the difference grows with increased distance from the melting point.

Boiling point of water

Graph of water vapor pressure versus temperature. At the normal boiling point of 100 °C, it equals the standard atmospheric pressure of 760 torr or 101.325 kPa.
Main page: Physics:Vapour pressure of water

Like all liquids, water boils when its vapor pressure reaches its surrounding pressure. In nature, the atmospheric pressure is lower at higher elevations and water boils at a lower temperature. The boiling temperature of water for atmospheric pressures can be approximated by the Antoine equation:

[math]\displaystyle{ \log_{10}\left(\frac{P}{1\text{ Torr}}\right) = 8.07131 - \frac{1730.63\ {}^\circ\text{C}}{233.426\ {}^\circ\text{C} + T_b} }[/math]

or transformed into this temperature-explicit form:

[math]\displaystyle{ T_b = \frac{1730.63\ {}^\circ\text{C}}{8.07131 - \log_{10}\left(\frac{P}{1\text{ Torr}}\right)} - 233.426\ {}^\circ\text{C} }[/math]

where the temperature [math]\displaystyle{ T_b }[/math] is the boiling point in degrees Celsius and the pressure [math]\displaystyle{ P }[/math] is in torr.

Dühring's rule

Main page: Chemistry:Dühring's rule

Dühring's rule states that a linear relationship exists between the temperatures at which two solutions exert the same vapor pressure.

Examples

The following table is a list of a variety of substances ordered by increasing vapor pressure (in absolute units).

Substance Vapor pressure Temperature
(°C)
(Pa) (bar) (mmHg)
Octaethylene glycol[10] 9.2×10−8 Pa 9.2×10−13 6.9×10−10 89.85
Glycerol 0.4 Pa 0.000004 0.003 50
Mercury 1 Pa 0.00001 0.0075 41.85
Tungsten 1 Pa 0.00001 0.0075 3203
Xenon difluoride 600 Pa 0.006 4.50 25
Water (H2O) 2.3 kPa 0.023 17.5 20
Propanol 2.4 kPa 0.024 18.0 20
Methyl isobutyl ketone 2.66 kPa 0.0266 19.95 25
Iron pentacarbonyl 2.80 kPa 0.028 21 20
Ethanol 5.83 kPa 0.0583 43.7 20
Freon 113 37.9 kPa 0.379 284 20
Acetaldehyde 98.7 kPa 0.987 740 20
Butane 220 kPa 2.2 1650 20
Formaldehyde 435.7 kPa 4.357 3268 20
Propane[11] 997.8 kPa 9.978 7584 26.85
Carbonyl sulfide 1.255 MPa 12.55 9412 25
Nitrous oxide[12] 5.660 MPa 56.60 42453 25
Carbon dioxide 5.7 MPa 57 42753 20

Estimating vapor pressure from molecular structure

Several empirical methods exist to estimate the vapor pressure from molecular structure for organic molecules. Some examples are SIMPOL.1 method,[13] the method of Moller et al.,[9] and EVAPORATION (Estimation of VApour Pressure of ORganics, Accounting for Temperature, Intramolecular, and Non-additivity effects).[14][15]

Meaning in meteorology

In meteorology, the term vapor pressure means the partial pressure of water vapor in the atmosphere, even if it is not in equilibrium.[16] This differs from its meaning in other sciences.[16] According to the American Meteorological Society Glossary of Meteorology, saturation vapor pressure properly refers to the equilibrium vapor pressure of water above a flat surface of liquid water or solid ice, and is a function only of temperature and whether the condensed phase is liquid or solid.[17] Relative humidity is defined relative to saturation vapor pressure.[18] Equilibrium vapor pressure does not require the condensed phase to be a flat surface; it might consist of tiny droplets possibly containing solutes (impurities), such as a cloud.[19][18] Equilibrium vapor pressure may differ significantly from saturation vapor pressure depending on the size of droplets and presence of other particles which act as cloud condensation nuclei.[19][18]

However, these terms are used inconsistently, and some authors use "saturation vapor pressure" outside the narrow meaning given by the AMS Glossary. For example, a text on atmospheric convection states, "The Kelvin effect causes the saturation vapor pressure over the curved surface of the droplet to be greater than that over a flat water surface" (emphasis added).[20]

The still-current term saturation vapor pressure derives from the obsolete theory that water vapor dissolves into air, and that air at a given temperature can only hold a certain amount of water before becoming "saturated".[18] Actually, as stated by Dalton's law (known since 1802), the partial pressure of water vapor or any substance does not depend on air at all, and the relevant temperature is that of the liquid.[18] Nevertheless, the erroneous belief persists among the public and even meteorologists, aided by the misleading terms saturation pressure and supersaturation and the related definition of relative humidity.[18]

See also


Notes

  1. ↑ Spelled vapour pressure in the UK; see spelling differences.

References

  1. ↑ "Vapor Pressure of Organic Compounds. Measurement and Correlation". http://www.capec.kt.dtu.dk/documents/overview/Vapor-pressure-Ruzicka.pdf. 
  2. ↑ 2.0 2.1 What is the Antoine Equation? (Chemistry Department, Frostburg State University, Maryland)
  3. ↑ 3.0 3.1 Sinnot, R.K. (2005). Chemical Engineering Design] (4th ed.). Butterworth-Heinemann. p. 331. ISBN 978-0-7506-6538-4. https://books.google.com/books?id=DJaxUL3numgC&pg=PA331. 
  4. ↑ Wagner, W. (1973), "New vapour pressure measurements for argon and nitrogen and a new method for establishing rational vapour pressure equations", Cryogenics 13 (8): 470–482, doi:10.1016/0011-2275(73)90003-9, Bibcode: 1973Cryo...13..470W 
  5. ↑ Perry's Chemical Engineers' Handbook, 7th Ed. pp. 4–15
  6. ↑ Perry, R.H., ed (1997). Perry's Chemical Engineers' Handbook (7th ed.). McGraw-Hill. ISBN 978-0-07-049841-9. 
  7. ↑ Petrucci, Ralph H.; Harwood, William S.; Herring, F.Geoffrey (2002). General Chemistry (8th ed.). Prentice Hall. p. 484. ISBN 978-0-13-014329-7. https://archive.org/details/generalchemistry00hill. 
  8. ↑ Dreisbach, R. R.; Spencer, R. S. (1949). "Infinite Points of Cox Chart Families and dt/dP Values at any Pressure". Industrial and Engineering Chemistry 41 (1): 176. doi:10.1021/ie50469a040. 
  9. ↑ 9.0 9.1 Moller B.; Rarey J.; Ramjugernath D. (2008). "Estimation of the vapour pressure of non-electrolyte organic compounds via group contributions and group interactions". Journal of Molecular Liquids 143: 52–63. doi:10.1016/j.molliq.2008.04.020. 
  10. ↑ Krieger, Ulrich K.; Siegrist, Franziska; Marcolli, Claudia; Emanuelsson, Eva U.; Gøbel, Freya M.; Bilde, Merete (8 January 2018). "A reference data set for validating vapor pressure measurement techniques: homologous series of polyethylene glycols". Atmospheric Measurement Techniques (Copernicus Publications) 11 (1): 49–63. doi:10.5194/amt-11-49-2018. ISSN 1867-1381. Bibcode: 2018AMT....11...49K. https://amt.copernicus.org/articles/11/49/2018/amt-11-49-2018.pdf. Retrieved 7 April 2022. 
  11. ↑ "Thermophysical Properties Of Fluids II – Methane, Ethane, Propane, Isobutane, And Normal Butane" (page 110 of PDF, page 686 of original document), BA Younglove and JF Ely.
  12. ↑ "Thermophysical Properties Of Nitrous Oxide" (page 14 of PDF, page 10 of original document), ESDU.
  13. ↑ Pankow, J. F. (2008). "SIMPOL.1: a simple group contribution method for predicting vapor pressures and enthalpies of vaporization of multifunctional organic compounds". Atmos. Chem. Phys. 8 (10): 2773–2796. doi:10.5194/acp-8-2773-2008. Bibcode: 2008ACP.....8.2773P. 
  14. ↑ "Vapour pressure of Pure Liquid Organic Compounds: Estimation by EVAPORATION". 11 June 2014. http://tropo.aeronomie.be/models/evaporation_run.htm. 
  15. ↑ Compernolle, S. (2011). "EVAPORATION: a new vapour pressure estimation method for organic molecules including non-additivity and intramolecular interactions". Atmos. Chem. Phys. 11 (18): 9431–9450. doi:10.5194/acp-11-9431-2011. Bibcode: 2011ACP....11.9431C. http://www.atmos-chem-phys.net/11/9431/2011/acp-11-9431-2011.html. 
  16. ↑ 16.0 16.1 American Meteorological Society (2012). "vapor pressure". Glossary of Meteorology. https://glossary.ametsoc.org/wiki/Vapor_pressure. Retrieved 2022-11-28. 
  17. ↑ American Meteorological Society (2020). "saturation vapor pressure". Glossary of Meteorology. https://glossary.ametsoc.org/wiki/Saturation_vapor_pressure. Retrieved 2022-11-28. 
  18. ↑ 18.0 18.1 18.2 18.3 18.4 18.5 Babin, Steven M. (1998). "Relative Humidity & Saturation Vapor Pressure: A Brief Tutorial". Johns Hopkins University Applied Physics Laboratory. https://fermi.jhuapl.edu/people/babin/vapor/vapor.html.  (Alternate title: "Water Vapor Myths: A Brief Tutorial".)
  19. ↑ 19.0 19.1 American Meteorological Society (2012). "equilibrium vapor pressure". Glossary of Meteorology. https://glossary.ametsoc.org/wiki/Equilibrium_vapor_pressure. Retrieved 2022-11-28. 
  20. ↑ Raymond, David J. (2011-05-12). "Chapter 5: Cloud Microphysics". Atmospheric Convection. New Mexico Institute of Mining and Technology. p. 73. http://kestrel.nmt.edu/~raymond/classes/ph536/notes/microphys.pdf. Retrieved 2022-11-28. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Vapor_pressure&oldid=3416916"