Conical coordinates
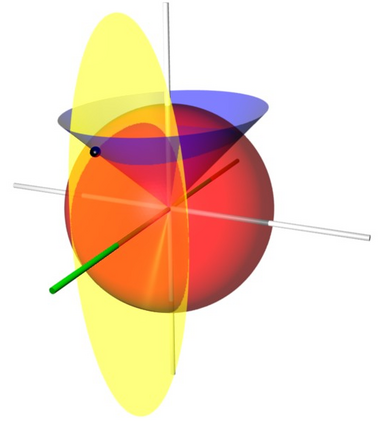
Conical coordinates, sometimes called sphero-conal or sphero-conical coordinates, are a three-dimensional orthogonal coordinate system consisting of concentric spheres (described by their radius r) and by two families of perpendicular elliptic cones, aligned along the z- and x-axes, respectively. The intersection between one of the cones and the sphere forms a spherical conic.
Basic definitions
The conical coordinates [math]\displaystyle{ (r, \mu, \nu) }[/math] are defined by
- [math]\displaystyle{ x = \frac{r\mu\nu}{bc} }[/math]
- [math]\displaystyle{ y = \frac{r}{b} \sqrt{\frac{\left( \mu^{2} - b^{2} \right) \left( \nu^{2} - b^{2} \right)}{\left( b^{2} - c^{2} \right)} } }[/math]
- [math]\displaystyle{ z = \frac{r}{c} \sqrt{\frac{\left( \mu^{2} - c^{2} \right) \left( \nu^{2} - c^{2} \right)}{\left( c^{2} - b^{2} \right)} } }[/math]
with the following limitations on the coordinates
- [math]\displaystyle{ \nu^{2} \lt c^{2} \lt \mu^{2} \lt b^{2}. }[/math]
Surfaces of constant r are spheres of that radius centered on the origin
- [math]\displaystyle{ x^{2} + y^{2} + z^{2} = r^{2}, }[/math]
whereas surfaces of constant [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ \nu }[/math] are mutually perpendicular cones
- [math]\displaystyle{ \frac{x^{2}}{\mu^{2}} + \frac{y^{2}}{\mu^{2} - b^{2}} + \frac{z^{2}}{\mu^{2} - c^{2}} = 0 }[/math]
and
- [math]\displaystyle{ \frac{x^{2}}{\nu^{2}} + \frac{y^{2}}{\nu^{2} - b^{2}} + \frac{z^{2}}{\nu^{2} - c^{2}} = 0. }[/math]
In this coordinate system, both Laplace's equation and the Helmholtz equation are separable.
Scale factors
The scale factor for the radius r is one (hr = 1), as in spherical coordinates. The scale factors for the two conical coordinates are
- [math]\displaystyle{ h_{\mu} = r \sqrt{\frac{\mu^{2} - \nu^{2}}{\left( b^{2} - \mu^{2} \right) \left( \mu^{2} - c^{2} \right)}} }[/math]
and
- [math]\displaystyle{ h_{\nu} = r \sqrt{\frac{\mu^{2} - \nu^{2}}{\left( b^{2} - \nu^{2} \right) \left( c^{2} - \nu^{2} \right)}}. }[/math]
References
Bibliography
- Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 659. ISBN 0-07-043316-X.
- Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 183–184. https://archive.org/details/mathematicsofphy0002marg.
- Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 179. ASIN B0000CKZX7.
- Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. pp. 991–100.
- Arfken G (1970). Mathematical Methods for Physicists (2nd ed.). Orlando, FL: Academic Press. pp. 118–119. ASIN B000MBRNX4.
- Moon P, Spencer DE (1988). "Conical Coordinates (r, θ, λ)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed.). New York: Springer-Verlag. pp. 37–40 (Table 1.09). ISBN 978-0-387-18430-2.
External links
 |

